Bài giảng Toán tổ hợp - Chương 4: Đại cương về đồ thị

ĐẠI CƯƠNG VỀ ĐỒ THỊ 
Chương 4. 
2 
Nội dung 
1. Giới thiệu 
2. Các khái niệm cơ bản 
3. Biểu diễn đồ thị 
4. Đẳng cấu đồ thị 
5. Đường đi, chu trình 
3 
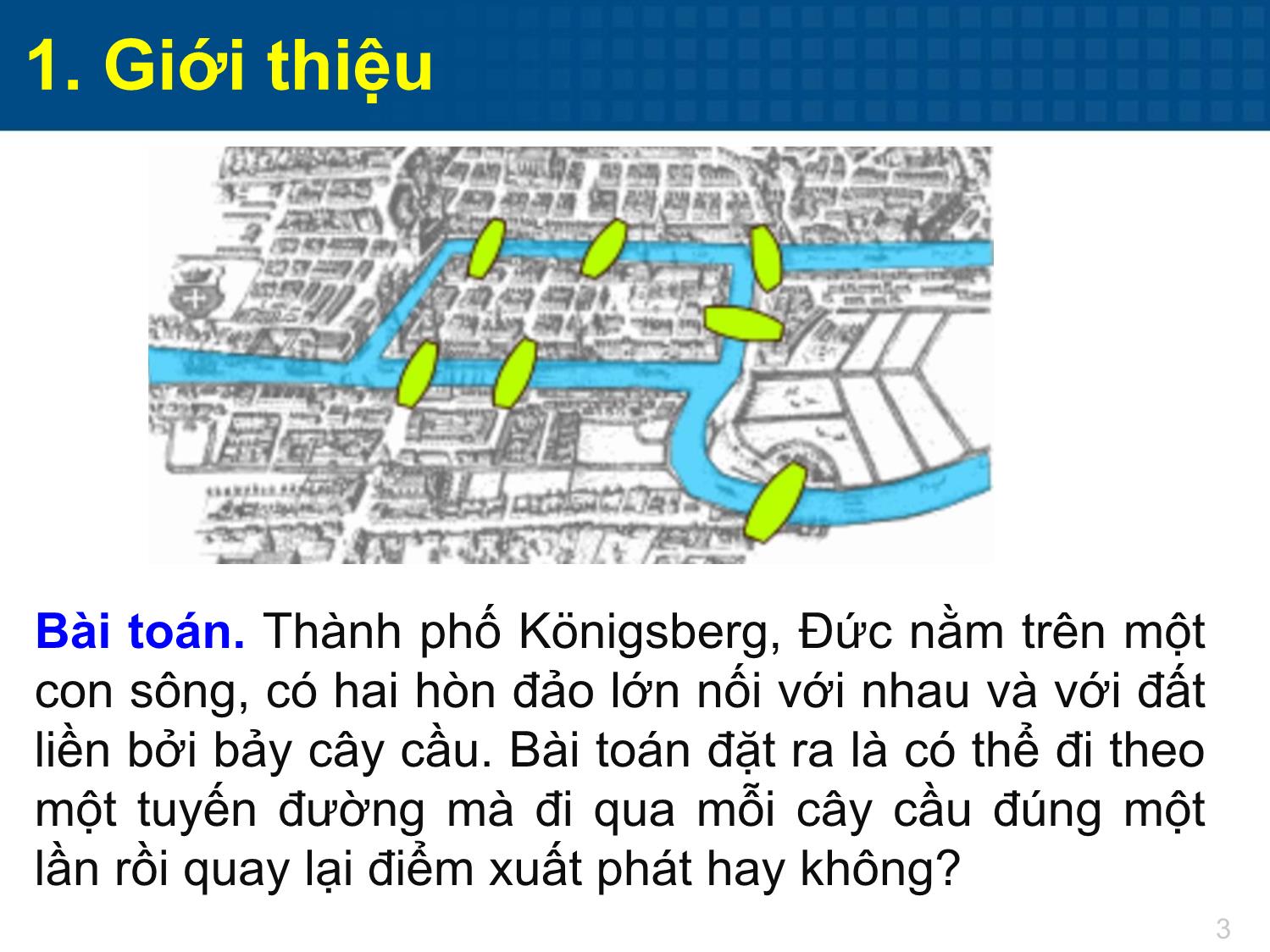
Bài toán. Thành phố Königsberg, Đức nằm trên một 
con sông, có hai hòn đảo lớn nối với nhau và với đất 
liền bởi bảy cây cầu. Bài toán đặt ra là có thể đi theo 
một tuyến đường mà đi qua mỗi cây cầu đúng một 
lần rồi quay lại điểm xuất phát hay không? 
1. Giới thiệu 
4 
Năm 1736, nhà toán học 
Leonhard Euler đã chứng 
minh rằng điều đó là không 
thể được. 
5 
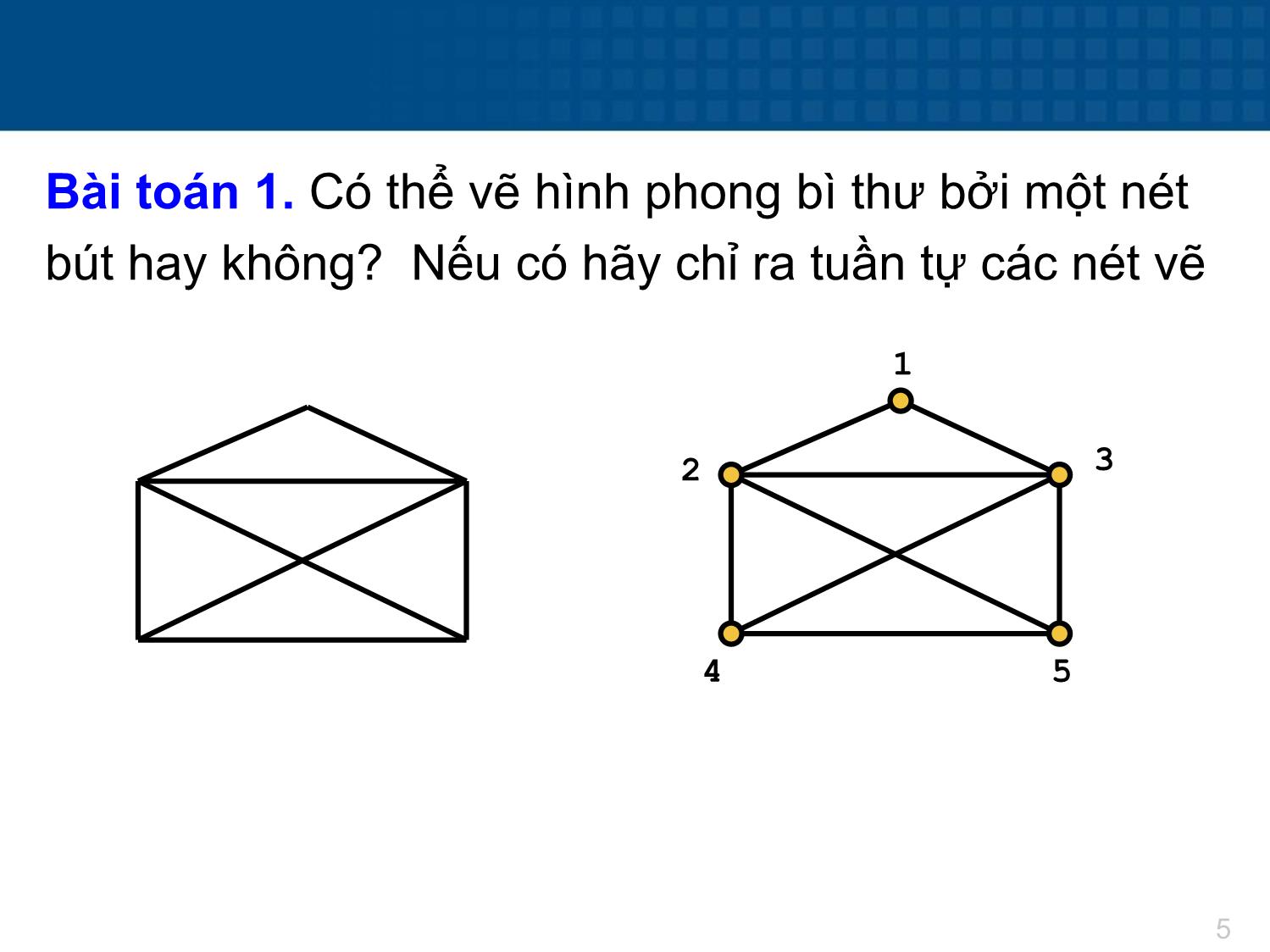
Bài toán 1. Có thể vẽ hình phong bì thư bởi một nét 
bút hay không? Nếu có hãy chỉ ra tuần tự các nét vẽ 
1 
3 2 
4 5 
6 
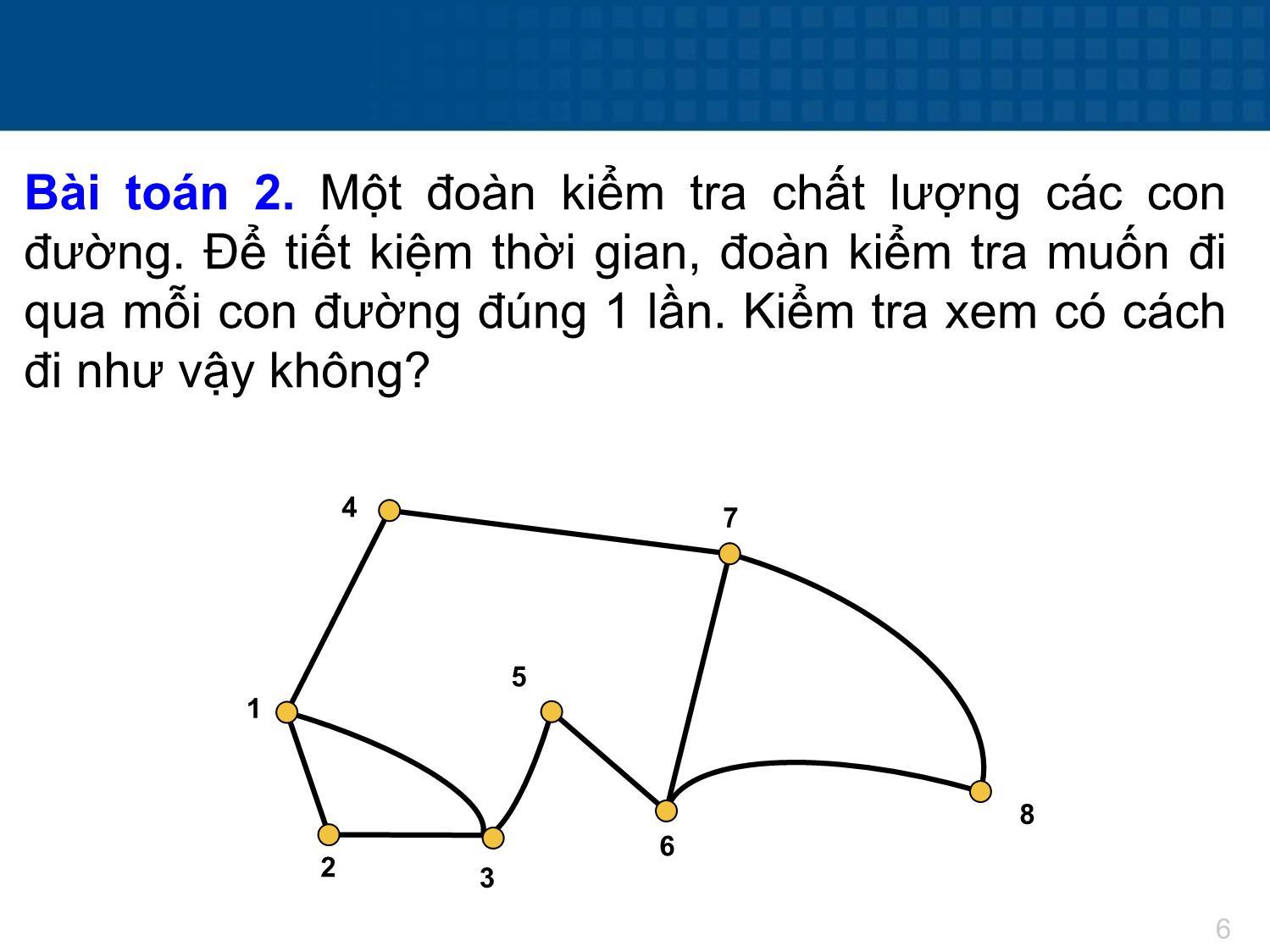
Bài toán 2. Một đoàn kiểm tra chất lượng các con 
đường. Để tiết kiệm thời gian, đoàn kiểm tra muốn đi 
qua mỗi con đường đúng 1 lần. Kiểm tra xem có cách 
đi như vậy không? 
2 
1 
3 
4 
5 
6 
7 
8 
7 
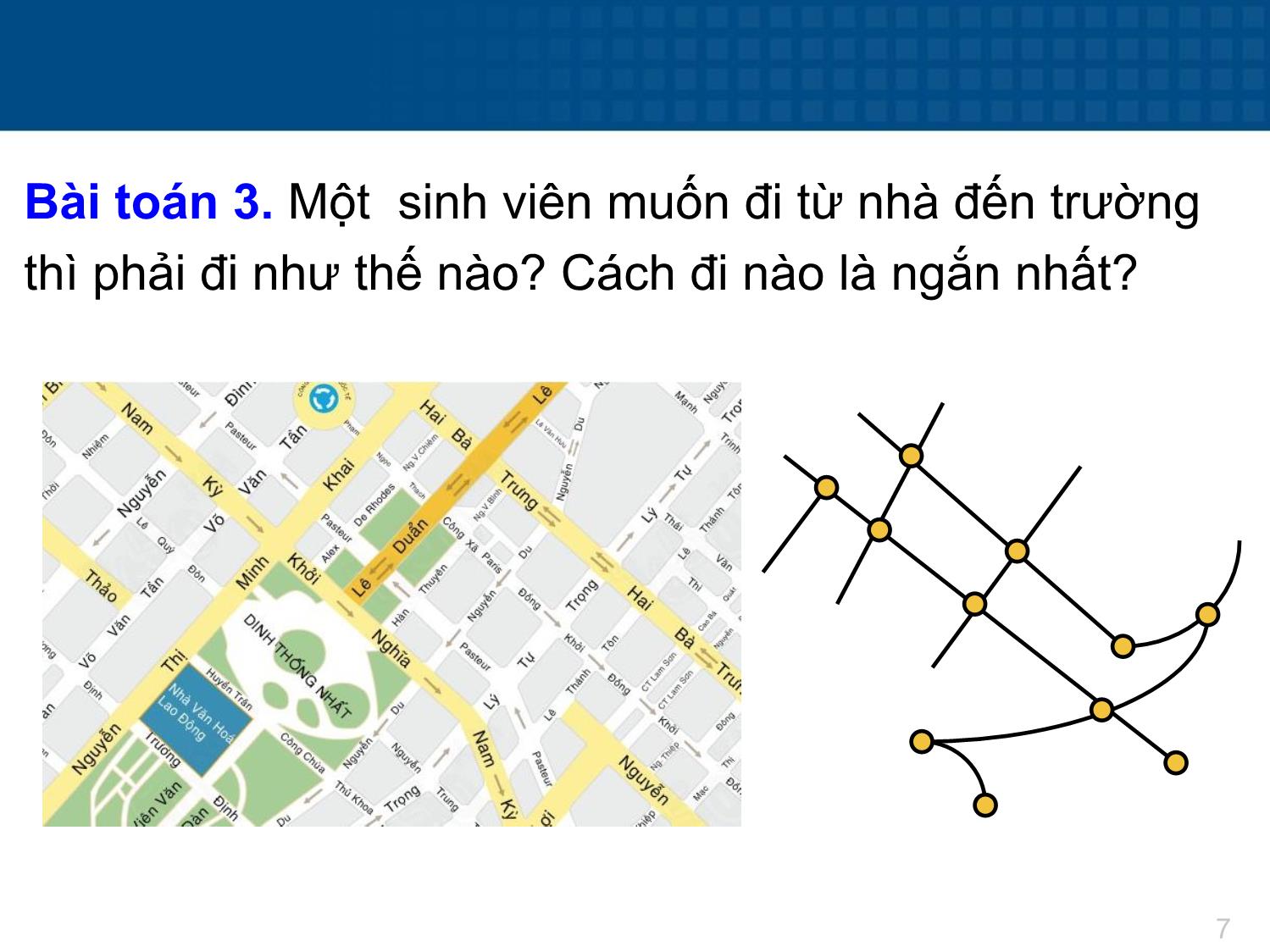
Bài toán 3. Một sinh viên muốn đi từ nhà đến trường 
thì phải đi như thế nào? Cách đi nào là ngắn nhất? 
8 
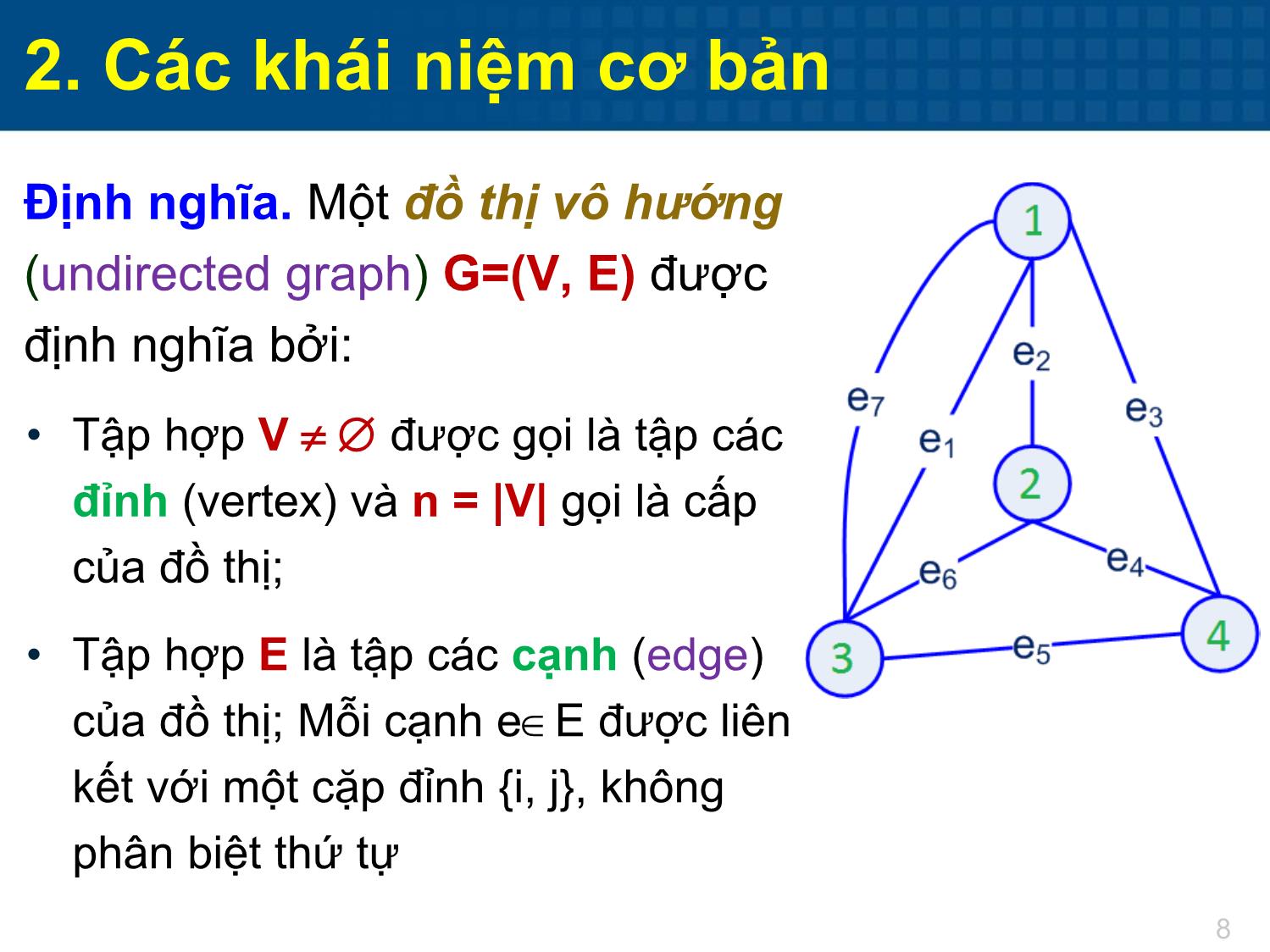
Định nghĩa. Một đồ thị vô hướng 
(undirected graph) G=(V, E) được 
định nghĩa bởi: 
• Tập hợp V  được gọi là tập các 
đỉnh (vertex) và n = |V| gọi là cấp 
của đồ thị; 
• Tập hợp E là tập các cạnh (edge) 
của đồ thị; Mỗi cạnh e E được liên 
kết với một cặp đỉnh {i, j}, không 
phân biệt thứ tự 
2. Các khái niệm cơ bản 
9 
Định nghĩa. Trên đồ thị vô hướng, xét cạnh e được 
liên kết với cặp đỉnh {i, j}: 
 Cạnh e kề với đỉnh i và đỉnh j (hay đỉnh i và đỉnh j kề 
với cạnh e); có thể viết tắt e=ij 
 Đỉnh i và đỉnh j được gọi là 2 đỉnh kề nhau (hay đỉnh i 
kề với đỉnh j và ngược lại, đỉnh j kề với đỉnh i) 
 Hai cạnh nối cùng một cặp đỉnh gọi là hai cạnh song 
song. 
 Cạnh có hai đỉnh trùng nhau gọi là một khuyên 
Đỉnh kề 
10 
( ) { : ( , ) }v u V v u E 
Tập các đỉnh kề với đỉnh v được viết là 
Nhận xét. Đồ thị G hoàn toàn được xác định nếu 
chúng ta biết 
Vvv  ),(
nên đồ thị G cũng có thể định nghĩa như sau: 
( , )G V 
Đỉnh kề 
11 
 Cạnh song song: e1, e7 
 Khuyên: e9 
 Đỉnh treo: 5 
 Đỉnh cô lập: 6 
 
(2) {1, 3, 4} 
Đỉnh kề 
12 
Định nghĩa. Cho G là đồ thị vô hướng. Khi đó G 
được gọi là: 
a) đơn đồ thị (hay đồ thị đơn) nếu G không có 
khuyên và không có cạnh song song 
b) đa đồ thị nếu G không có khuyên, cho phép có 
cạnh song song 
c) giả đồ thị nếu G cho phép có cạnh song song và 
có khuyên 
Một số loại đồ thị vô hướng 
13 
b 
d a 
k 
e 
h 
g 
c 
a 
b 
c d 
b 
c 
a 
d 
14 
 Đồ thị rỗng: tập cạnh là tập rỗng 
 Đồ thị đủ: đồ thị vô hướng, đơn, 
giữa hai đỉnh bất kỳ đều có đúng 
một cạnh. 
 Đồ thị đủ n đỉnh ký hiệu là Kn. 
 Kn có 
𝑛 n−1
2
 cạnh. 
 Đồ thị k-đều: là đồ thị mà mọi đỉnh 
đều có bậc bằng nhau và bằng k. 
C 
A B 
Các dạng đồ thị 
15 
 Đồ thị lưỡng phân: đồ thị vô 
hướng G=(V, E) được gọi là đồ thị 
lưỡng phân nếu tập V được chia 
thành hai tập V1 và V2 thỏa: 
 V1 và V2 phân hoạch V; 
 Cạnh chỉ nối giữa V1 và V2. 
 Đồ thị lưỡng phân đủ: là đồ thị 
lưỡng phân thỏa điều kiện mỗi đỉnh 
trong V1 kề với mọi đỉnh trong V2. 
• V1=n và V2=m, ký hiệu Kn,m 
C 
A 
B 
D 
E 
16 GV: Döông Anh Ñöùc 16 
K4 
K4 
K3, 3 
K2, 3 
K2  K1, 1 
K3 
17 
Định nghĩa. Một đồ thị có hướng 
G=(V, U) được định nghĩa bởi: 
• Tập hợp V  được gọi là tập 
các đỉnh. 
• Tập hợp U là tập các cạnh (cung) 
của đồ thị; Mỗi cạnh u U được 
liên kết với một cặp đỉnh (i, j) V2. 
Ký hiệu u=(i,j) hoặc u=ij. 
Đồ thị có hướng 
18 
Trên đồ thị có hướng, xét cạnh u được liên kết với 
cặp đỉnh (i, j): 
 i được gọi là đỉnh đầu, j được gọi là đỉnh cuối 
 Cạnh u kề với đỉnh i và đỉnh j (hay đỉnh i và đỉnh j 
kề với cạnh u); có thể viết tắt u=(i, j). Cạnh u đi ra 
khỏi đỉnh i và đi vào đỉnh j. 
Đỉnh kề 
19 
( ), ( )v v  
Định nghĩa. Cho đồ thị có hướng G=(V, E) và e=(u, v) E 
• v là đỉnh sau của u 
• u là đỉnh trước của v 
• Tập hợp các đỉnh sau và đỉnh trước của v lần lượt là 
Nhận xét. Đồ thị G hoàn toàn được xác định 
nếu chúng ta biết 
Vvv  ),(
nên đồ thị G cũng có thể được định nghĩa như sau: 
),(  VG
Đỉnh kề 
20 
)(v
Ví dụ. 
 1 
2 
3 5 
6 
4 
a 
b 
c 
d 
e 
f 
g 
h 
i 
j k 
l 
v 
1 
2 
3 
5 
6 
)(v 
Đỉnh kề 
21 
 Cạnh song song 
- u1, u7 cùng chiều 
- u5, u8 ngược chiều 
 Khuyên: u2 
 Đỉnh treo: 6 
 Đỉnh cô lập: 5 
22 
 Đồ thị có tập đỉnh và tập cạnh hữu hạn được gọi 
là đồ thị hữu hạn 
 Trong học phần này ta chỉ làm việc với các đồ thị 
hữu hạn. Để ngắn gọn chúng ta chỉ dùng thuật 
ngữ ĐỒ THỊ và hiểu ngầm đó là đồ thị hữu hạn. 
Đồ thị hữu hạn 
23 
Định nghĩa. Cho hai đồ thị G = (V,E) và G’ = (V’,E’) 
(cùng vô hướng hoặc cùng có hướng). 
 G’ được gọi là đồ thị con của G, ký hiệu G’ G, 
nếu V’ V và E’  E 
 Nếu V’= V và E’  E thì G’ được gọi là đồ thị con 
khung của G. 
Đồ thị con 
G H 
24 
Định nghĩa. Xét đồ thị vô 
hướng G. Bậc của đỉnh x 
trong đồ thị G là số các cạnh 
kề với đỉnh x, mỗi khuyên 
được tính hai lần, ký hiệu là 
degG(x) (hay deg(x)