Bài giảng Toán rời rạc - Chương I: Cơ sở lôgic
Mệnh đề
Định nghĩa: Mệnh đề là một khẳng định có giá trị chân lý xác định, đúng hoặc sai.
Câu hỏi, câu cảm thán, mệnh lệnh không là mệnh đề.
Ví dụ:
- Đại học CNTT trực thuộc ĐHQG TP.HCM.
- 1+7 =8.
- Hôm nay em đẹp quá! (không là mệnh đề)
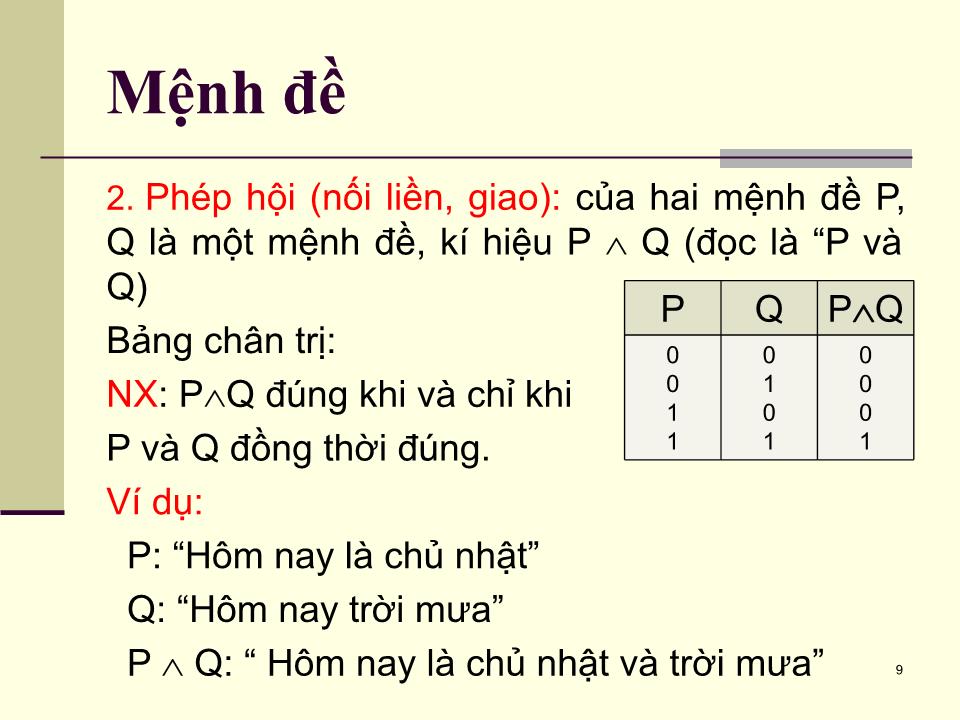
- Hôm nay ngày thứ mấy? (không là mệnh đề

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương I: Cơ sở lôgic", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương I: Cơ sở lôgic

CẤU TRÚC RỜI RẠC 1 CHƯƠNG I: CƠ SỞ LÔGIC Mệnh đề Biểu thức logic (Dạng mệnh đề) Qui tắc suy diễn Vị từ, lượng từ Quy nạp toán học 2 “Toan tính của chiến lược gia 44 tuổi đã suýt thành công nếu ông không tính tới đột biến từ những ngôi sao đối phương”. Nguồn: 3 Mệnh đề Định nghĩa: Mệnh đề là một khẳng định có giá trị chân lý xác định, đúng hoặc sai. Câu hỏi, câu cảm thán, mệnh lệnh không là mệnh đề. Ví dụ: - Đại học CNTT trực thuộc ĐHQG TP.HCM. - 1+ 7 = 8. - Hôm nay em đẹp quá! (k hông là mệnh đề) - Hôm nay ngày thứ mấy? (k hông là mệnh đề) 4 Mệnh đề Ký hiệu: người ta dùng các ký hiệu P, Q, R (p,q,r,) để chỉ mệnh đề. Chân trị của mệnh đề: Một mệnh đề chỉ có thể đúng hoặc sai, không thể đồng thời vừa đúng vừa sai. Khi mệnh đề P đúng ta nói P có chân trị đúng, ngược lại ta nói P có chân trị sai. Chân trị đúng và chân trị sai sẽ được ký hiệu lần lượt là 1(hay Đ,T) và 0(hay S,F) 5 Mệnh đề Phân loại: gồm 2 loại Mệnh đề phức hợp: là mệnh đề được xây dựng từ các mệnh đề khác nhờ liên kết bằng các liên từ (và, hay, khi và chỉ khi,) hoặc trạng từ “không” Mệnh đề sơ cấp (nguyên thủy): Là mệnh đề không thể xây dựng từ các mệnh đề khác thông qua liên từ hoặc trạng từ “không” 6 Mệnh đề Ví dụ: - 2 là số nguyên tố . - 2 không l à số nguyên tố . - 2 là số nguyên tố và là số lẻ. - An đang xem ti vi hay đang học bài. 7 Các phép toán : có 5 phép toán Phép phủ định: phủ định của mệnh đề P là một mệnh đề, ký hiệu là P hay (đọc là “không” P hay “phủ định c ủa” P ) . Bảng chân trị : Ví dụ: - 2 là số nguyên tố . Phủ định: 2 không là số nguyên tố - 15 > 5 Phủ định: 1 5 ≤ 5 P 0 1 1 0 Mệnh đề 8 Phép hội (nối liền, giao): của hai mệnh đề P, Q là một mệnh đề, kí hiệu P Q (đọc là “P và Q ) Bảng chân trị : NX : P Q đúng khi và chỉ khi P và Q đồng thời đúng. Ví dụ: P: “Hôm nay là chủ nhật” Q: “Hôm nay trời mưa” P Q : “ Hôm nay là chủ nhật và trời mưa” P Q P Q 0 0 1 1 0 1 0 1 0 0 0 1 Mệnh đề 9 Phép tuyển (nối rời, hợp): của hai mệnh đề P, Q là mộ t mệnh đề, kí hiệu P Q (đọc là “P hay Q”) . Bảng chân trị : NX: P Q sai khi và chỉ khi P và Q đồng thời sai. Ví dụ: - e > 4 hay e > 5 (S) - 2 là số nguyên tố hay là số lẻ (Đ) P Q P Q 0 0 1 1 0 1 0 1 0 1 1 1 Mệnh đề 10 Phép kéo theo: Mệnh đề P kéo theo mệnh đề Q là một mệnh đề, kí hiệu P Q (đọc là “P kéo theo Q” hay “Nếu P thì Q” hay “P là điều kiện đủ của Q” hay “Q là điều kiện cần của P”) . Bảng chân trị : NX: P Q sai khi và chỉ khi P đúng mà Q sai. Ví dụ: e >4 kéo theo 5>6 P Q P Q 0 0 1 1 0 1 0 1 1 1 0 1 Mệnh đề 11 Phép kéo theo hai chiều (phép tương đương) : Mệnh đề P kéo theo mệnh đề Q và ngược lại (mệnh đề P tương đương với mệnh đề Q) là một mệnh đề , ký hiệu P Q (đọc là “P nếu và chỉ nếu Q” hay “P khi và chỉ khi Q” hay “P là điều kiện cần và đủ của Q”) . Bảng chân trị : NX: P Q đúng khi và chỉ khi P và Q có cùng chân trị Ví dụ: 6 chia hết cho 3 khi v à chỉ khi 6 chia hết cho 2 P Q P Q 0 0 1 1 0 1 0 1 1 0 0 1 Mệnh đề 12 Định nghĩa: B iểu thức logic được cấu tạo từ: - Các mệnh đề (các hằng mệnh đề) - Các biến mệnh đề p, q, r, , tức là các biến lấy giá trị là các mệnh đề nào đó - Các phép toán logic , , , , và dấu đóng mở ngoặc () để chỉ rõ thứ tự thực hiện của các phép toán. Ví dụ: E(p,q) = ( p q) F(p,q,r) = (p q) (q r) Biểu thức logic (Dạng mệnh đề) 13 Độ ưu tiên của các toán tử logic: - Ưu tiên mức 1: () - Ưu tiên mức 2: - Ưu tiên mức 3: , - Ưu tiên mức 4: , Bảng chân trị của một biểu thức logic: là bảng liệt kê chân trị c ủa biểu thức logic theo các trường hợp về chân trị của tất cả các biến mệnh đề trong biểu thức logic hay theo các bộ giá trị của bộ biến mệnh đề . Biểu thức logic 14 Bảng chân trị của một biểu thức logic. Ví dụ: Với một biến mệnh đề, ta có hai trường hợp là 0 hoặc 1. Với hai biến mệnh đề p,q ta có bốn trường hợp chân trị của bộ biến (p,q) là các bộ giá trị (0,0), (0,1), (1,0) và (1,1). NX: Trong trường hợp tổng quát, n ếu có n biến mệnh đề thì ta có trường hợp chân trị cho b ộ n biến. Biểu thức logic 15 Ví dụ: Cho E(p,q,r) =(p q) r . Ta có bảng chân trị sau: Biểu thức logic 16 p q r p q (p q) r 0 0 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1 1 1 1 Tương đương logic: Hai biểu thức logic E và F theo các biến mệnh đề nào đó được gọi là tương đương logic nếu chúng có cùng bảng chân trị. Ký hiệu : E F (E tương đương với F). Ví dụ : (p q) p q Biểu thức logic E được gọi là hằng đúng nếu chân trị của E luôn bằng 1 (đúng) trong mọi trường hợp về chân trị của các biến mệnh đề có trong E. Nói cách khác, E là hằng đú
File đính kèm:
 bai_giang_cau_truc_roi_rac_chuong_i_co_so_logic.pptx
bai_giang_cau_truc_roi_rac_chuong_i_co_so_logic.pptx

