Bài giảng Toán rời rạc - Chương 6: Cây
Một số khái niệm cơ bản
Định lý Daisy Chain
T là đồ thị có n đỉnh. Các mệnh đề tương đương:
- T là một cây
- T không có chu trình và có n-1 cạnh
- T liên thông, mọi cạnh đều là cầu
- Giữa hai đỉnh bất kỳ của T luôn tồn tại một đường đi sơ cấp duy nhất
- T không có chu trình và nếu thêm một cạnh mới nối 2 đỉnh bất kỳ của T thì sẽ tao ra một chu trình
- T liên thông và có n-1 cạnh
Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
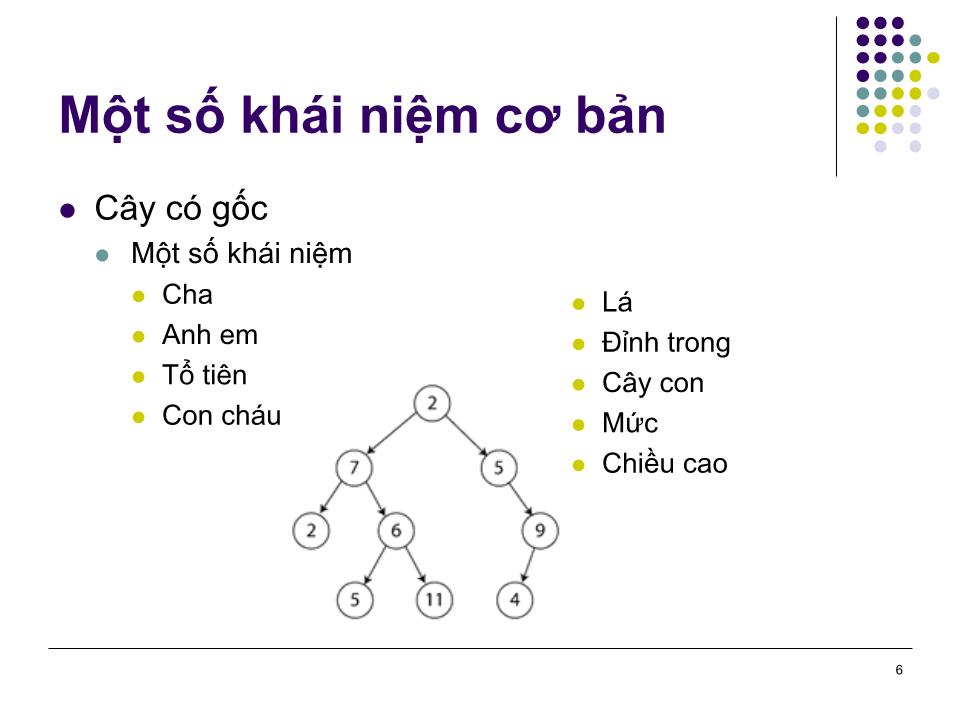
Trang 6

Trang 7

Trang 8
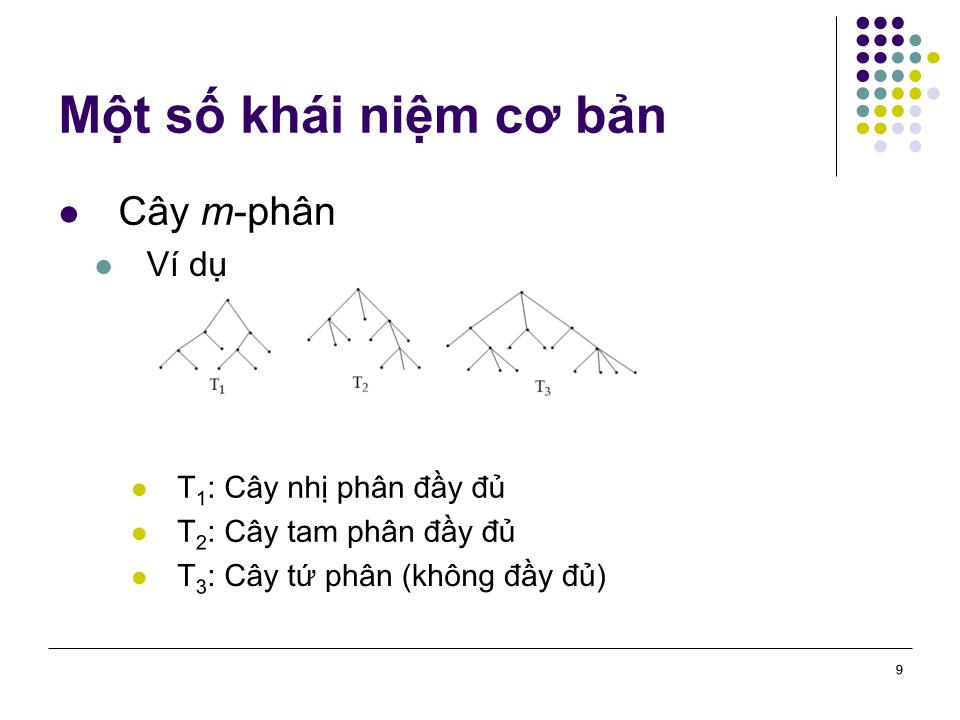
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương 6: Cây", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương 6: Cây
1 CHƯƠNG 6: CÂY Một số khái niệm cơ bản Cây m – phân và các tính chất Phép duyệt cây nhị phân Ký pháp nghịch đảo Ba Lan Thuật toán Prim và Kruskal tìm cây khung nhỏ nhất trong đồ thị liên thông có trọng số 2 Một số khái niệm cơ bản Cây Định nghĩa: Cây là một đồ thị vô hướng , liên thông và không có chu trình sơ cấp Cây không có cạnh bội và khuyên Cây là một đơn đồ thị Ví dụ 3 Một số khái niệm cơ bản Rừng Định nghĩa: Rừng là một đồ thị vô hướng và không có chu trình Rừng có thể có nhiều thành phần liên thông Mỗi thành phần liên thông là một cây Ví dụ 4 Một số khái niệm cơ bản Định lý (Điều kiện đủ của cây) Nếu mọi cặp đỉnh của một đồ thị vô hướng G luôn tồn tại một đường đi sơ cấp duy nhất thì G là một cây. (Chứng minh SV tham khảo tài liệu) 5 Một số khái niệm cơ bản Cây có gốc Định nghĩa Một cây với một đỉnh được chọn làm gốc Định hướng các cạnh trên cây từ gốc đi ra Ví dụ Cùng một cây, nếu chọn gốc khác nhau thì cây có gốc thu được sẽ khác nhau 6 Một số khái niệm cơ bản Cây có gốc Một số khái niệm Cha Anh em Tổ tiên Con cháu Lá Đỉnh trong Cây con Mức Chiều cao 7 Một số khái niệm cơ bản Định lý Daisy Chain T là đồ thị có n đỉnh. Các mệnh đề tương đương: T là một cây T không có chu trình và có n -1 cạnh T liên thông, mọi cạnh đều là cầu Giữa hai đỉnh bất kỳ của T luôn tồn tại một đường đi sơ cấp duy nhất T không có chu trình và nếu thêm một cạnh mới nối 2 đỉnh bất kỳ của T thì sẽ tao ra một chu trình T liên thông và có n -1 cạnh 8 Một số khái niệm cơ bản Cây m -phân Định nghĩa Cây m-phân Cây có gốc Tất cả các đỉnh trong có không quá m con Cây m -phân đầy đủ Cây có gốc Tất cả các đỉnh trong có đúng m con m =2: Cây nhị phân 9 Một số khái niệm cơ bản Cây m -phân Ví dụ T 1 : Cây nhị phân đầy đủ T 2 : Cây tam phân đầy đủ T 3 : Cây tứ phân (không đầy đủ) 10 Một số tính chất của cây Tính chất 1: Cây n đỉnh (n 2) có ít nhất 2 đỉnh treo Tính chất 2: Cây m -phân đầy đủ với i đỉnh trong có n = m . i + 1 đỉnh Tính chất 3: Cho cây m -phân đầy đủ có n đỉnh, có i đỉnh trong và l lá. Khi đó: i = ( n - 1 )/ m l = [( m - 1 ) n + 1 ] / m l = ( m - 1) i + 1 n = l + i 11 Phép duyệt cây nhị phân Định nghĩa Duyệt cây Liệt kê tất cả các đỉnh của cây theo một thứ tự xác định, mỗi đỉnh một lần 3 phương pháp duyệt cây Duyệt tiền tự (Pre-Oder) Duyệt trung tự (In-Oder) Duyệt hậu tự (Post-Oder) Cả 3 phương pháp duyệt trên đều được định nghĩa đệ quy đối với cây nhị phân (mỗi nút có tối đa 2 con lần lượt được gọi là con trái và con phải của nút) 12 Phép duyệt cây nhị phân Định nghĩa Duyệt tiền tự Duyệt nút gốc Duyệt tiền tự con trái Duyệt tiền tự con phải 1 2 3 13 Phép duyệt cây nhị phân Định nghĩa Duyệt trung tự Duyệt trung tự con trái Duyệt nút gốc Duyệt trung tự con phải 2 1 3 14 Phép duyệt cây nhị phân Định nghĩa Duyệt hậu tự Duyệt hậu tự con trái Duyệt hậu tự con phải Duyệt nút gốc 3 1 2 15 Phép duyệt cây nhị phân Định nghĩa Ví dụ Duyệt tiền tự A B D E C F Duyệt trung tự D B E A C F Duyệt hậu tự D E B F C A A B C D E F 16 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Là cây nhị phân Mỗi nút trong biểu diễn cho một toán tử 2 ngôi Mỗi nút lá biểu diễn cho một toán hạng của biểu thức Nếu nút trong biểu diễn cho toán tử 2 ngôi và có 2 con: Con trái biểu diễn cho biểu thức E 1 Con phải biểu diễn cho biểu thức E 2 khi đó nút trong này biểu diễn cho biểu thức E 1 E 2 17 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Ví dụ: E = (2 + 3)^2 – (4 – 1)*(15/5) 18 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Duyệt cây biểu thức Biểu thức tiền tố (duyệt tiền tự) - ^ + 2 3 2 * - 4 1 / 15 5 Biểu thức trung tố (duyệt trung tố) 2 + 3 ^ 2 - 4 - 1 * 15 / 5 Biểu thức hậu tố (duyệt hậu tố) 2 3 + 2 ^ 4 1 - 15 5 / * - 19 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Ký pháp nghịch đảo Ba Lan ( R everse P olish N otation – RPN) Biểu thức ở dạng hậu tố Sử dụng để tính giá trị biểu thức trên máy tính Tính từ trái qua phải Không sử dụng dấu ngoặc Sử dụng Stack (ngăn xếp) 20 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Ký pháp nghịch đảo Ba Lan ( R everse P olish N otation – RPN) Thuật toán tính giá trị biểu thức RPN Đọc một ký hiệu (token) Nếu ký hiệu là một số Đẩy vào Stack Ngược lại, ký hiệu là một toán tử Lấy ra 2 toán hạng từ Stack Tính giá trị theo toán tử đối với 2 toán hạng Đẩy kết quả vào Stack 21 Ký pháp nghịch đảo Ba Lan Cây biểu thức số học Ký pháp nghịch đảo Ba Lan ( R everse P olish N otation – RPN) Ví dụ: Tính giá trị biểu thức E = (2 + 3)^2 – (4 1)*(15/5) - Biểu thức nhập dưới dạng ký pháp RPN E = 2 3 + 2 ^ 4 1 - 15 5 / * - - Quá trình lưu trữ của cấu trúc Stack như sau: 22 Ký pháp nghịch đảo Ba Lan Ví dụ: E = 2 3 + 2 ^ 4 1 -
File đính kèm:
 bai_giang_cau_truc_roi_rac_chuong_6_cay.ppt
bai_giang_cau_truc_roi_rac_chuong_6_cay.ppt

