Bài giảng Toán rời rạc - Chương 3: Quan hệ

 3.1. Quan hệ hai ngôi trên một tập hợp và các 
tính chất. Biểu diễn quan hệ hai ngôi. 
 3.2. Quan hệ tương đương. Lớp tương đương. 
Sự phân hoạch thành các lớp tương đương. 
3.3. Quan hệ thứ tự. Thứ tự toàn phần và bán 
phần. Biểu đồ Hasse. Phần tử min và max. 
Các phần tử tối tiểu và tối đại. 
1 
Chương 3. Quan hệ 
2 
Quan hệ hai ngôi 
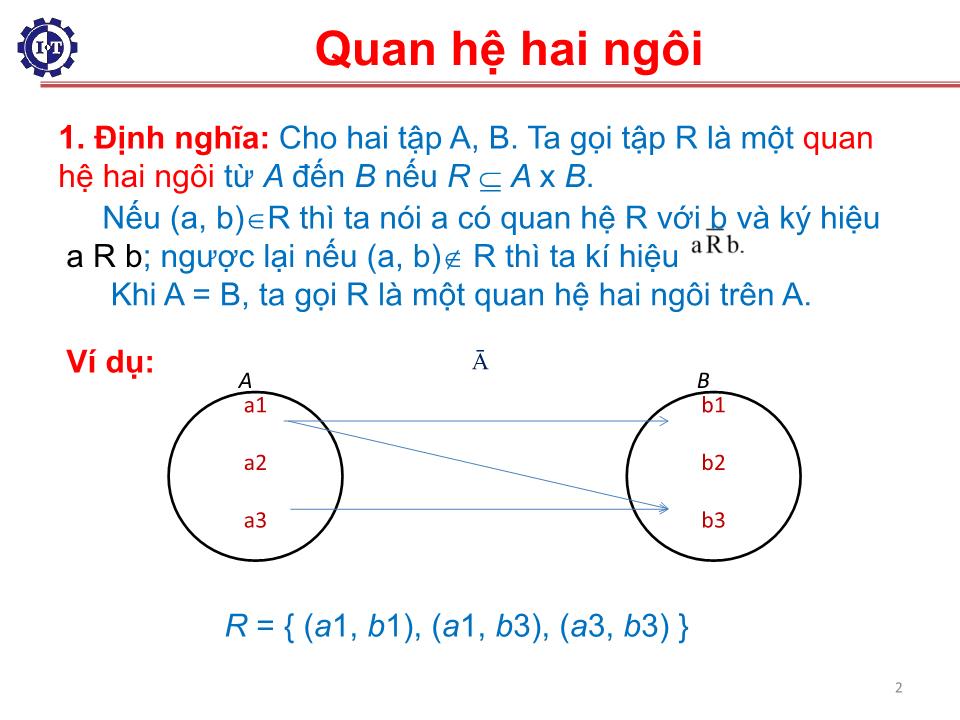
R = { ( a 1, b 1), ( a 1, b 3), ( a 3, b 3) } 
Định nghĩa: Cho hai tập A, B. Ta gọi tập R là m ột quan 
hệ hai ngôi từ A đến B nếu R  A x B . 
	Nếu (a, b) R thì ta nói a có quan hệ R với b và ký hiệu 
a R b ; ngược lại nếu (a, b) R thì ta kí hiệu 
 K hi A = B, ta gọi R là một quan hệ hai ngôi trên A. 
a1 
a2 
a3 
b1 
b2 
b3 
A 
B 
Ví dụ: 
Ā 
1. Định nghĩa. 
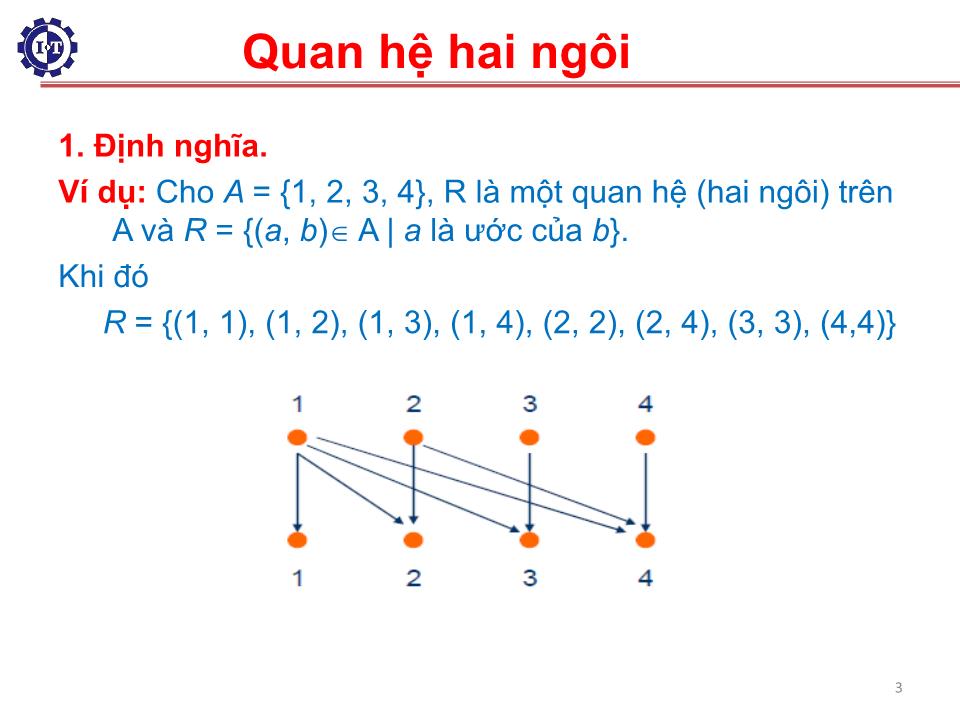
Ví dụ: Cho A = {1, 2, 3, 4}, R là một quan hệ (hai ngôi) trên A và R = {( a , b ) A | a là ước của b }. 
Khi đó 
 R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4,4)} 
3 
Quan hệ hai ngôi 
4 
2. Các tính chất của quan hệ. 
Định nghĩa : Giả sử R là một quan hệ hai ngôi trên tập A. 
 (a) Ta nói q uan hệ R có tính phản xạ nếu và chỉ nếu 
 	 a R a ,  a A . 
Ví dụ: Trên tập A = {1, 2, 3, 4}, quan hệ 
	R 1 = {(1,1), (1,2), (2,1), (2, 2), (3, 4), (4, 1), (4, 4)} 
không phản xạ vì (3, 3) R 1 
	R 2 = {(1,1), (1,2), (1,4), (2, 2), (3, 3), (4, 1), (4, 4)} phản xạ vì (1,1), (2, 2), (3, 3), (4, 4) R 2 
Quan hệ hai ngôi 
5 
2. Các tính chất của quan hệ 
Ví dụ: 
 - Quan hệ ≤ trên Z phản xạ vì a ≤ a,  a Z. 
 - Quan hệ > trên Z không phản xạ vì 1 không lớn hơn 1. 
 - Quan hệ “ | ” (“ước số”) trê n Z + là phản xạ vì mọi số 
nguyên dương a là ước của chính nó. 
Quan hệ hai ngôi 
6 
2. Các tính chất của quan hệ. 
Định nghĩa : Giả sử R là một quan hệ hai ngôi trên tập A. 
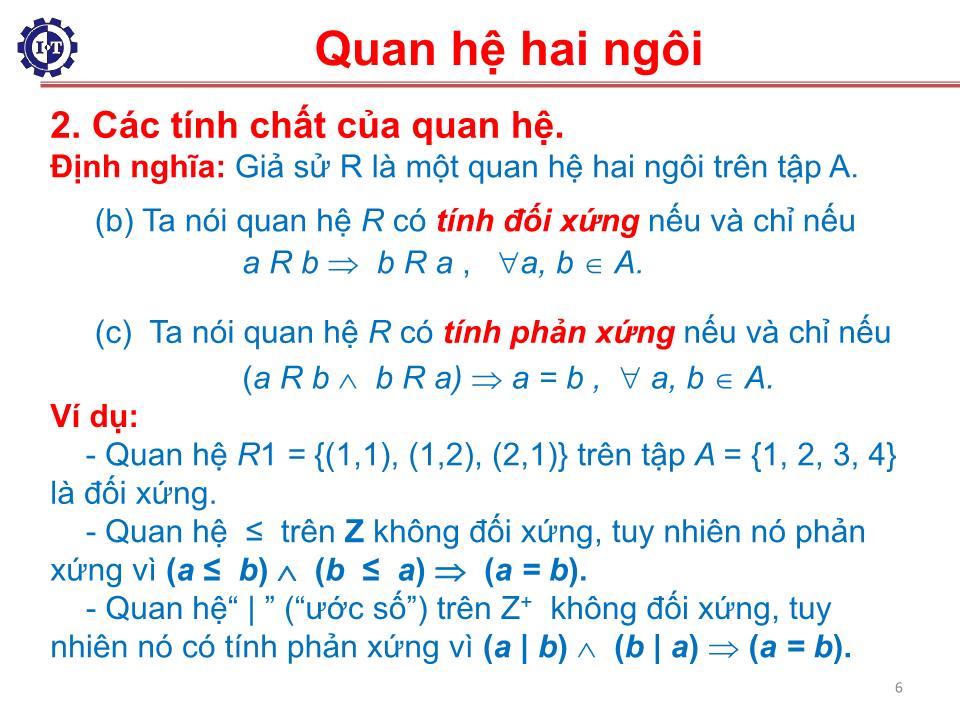
 (b) Ta nói q uan hệ R có tính đối xứng nếu và chỉ nếu 
 	 a R b b R a ,  a, b A. 
 (c) Ta nói q uan hệ R có tính phản xứng nếu và chỉ nếu 
	( a R b  b R a) a = b ,  a, b A. 
Ví dụ: 
 - Quan hệ R 1 = {(1,1), (1,2), (2,1)} trên tập A = {1, 2, 3, 4} là đối xứng. 
 - Quan hệ ≤ trên Z không đối xứng , tuy nhiên nó phản xứng vì ( a ≤ b )  ( b ≤ a ) ( a = b ). 
 - Quan hệ“ | ” (“ước số”) trên Z + không đối xứng , tuy nhiên nó có tính phản xứng vì ( a | b )  ( b | a ) ( a = b ). 
Quan hệ hai ngôi 
7 
2. Các tính chất của quan hệ 
Định nghĩa : Giả sử R là một quan hệ hai ngôi trên tập A. 
 (d) Ta nói q uan hệ R có tính bắc cầu (truyền) nếu và chỉ nếu 
	( a R b  b R c ) a R c ,  a,b,c A. 
Ví dụ: 
 - Quan hệ R = {(1,1), (1,2), (2,1), (2, 2), (1, 3), (2, 3)} 
trên tập A = {1, 2, 3, 4} có tính bắc cầu. 
 - Quan hệ ≤ và “|”trên Z có tính bắc cầu vì 
	( a ≤ b )  ( b ≤ c ) ( a ≤ c ) 
	( a | b )  ( b | c ) ( a | c ) 
Quan hệ hai ngôi 
8 
Đây là ma trận cấp 4×3 biễu diễn cho quan hệ R 
3. Biểu diễn quan hệ 
Định nghĩa. 
	 C ho R là quan hệ từ A = {1,2,3,4} đến B = {u,v,w} , 
R = {(1,u),(1,v),(2,w),(3,w),(4,u)}. 
	 Khi đó R có thể biễu diễn như sau 
Quan hệ hai ngôi 
3. Biểu diễn Quan hệ 
9 
Định nghĩa. Cho R là quan hệ từ A = { a 1 , a 2 , , a m } đến B = { b 1 , b 2 , , b n }. Ma trận biểu diễn của R là ma trận M R = [ m ij ] mxn xác định bởi : 
Ví dụ : Cho R là quan hệ từ A = {1, 2, 3} đến B = {1, 2}: a R b a > b . Khi đó ma trận biểu diễn của R là : 
Quan hệ hai ngôi 
3. Biểu diễn quan hệ 
10 
Ví dụ: Cho R là quan hệ từ A = { a 1 , a 2 , a 3 } đến B = { b 1 , b 2 , b 3 , b 4 , b 5 } được biễu diễn bởi ma trận 
Khi đó R gồm các cặp:{( a 1 , b 2 ), ( a 2 , b 1 ), ( a 2 , b 3 ), ( a 2 , b 4 ), ( a 3 , b 1 ), ( a 3 , b 3 ), ( a 3 , b 5 )}. 
Quan hệ hai ngôi 
3. Biểu diễn quan hệ 
Cho R là quan hệ trên tập A , khi đó M R là ma trận vuông . 
+) R là phản xạ nếu tất cả các phần tử trên đường chéo của M R đều bằng1: m ii = 1 ,  i . 
11 
Quan hệ hai ngôi 
3. Biểu diễn quan hệ 
+) R là đối xứng nếu M R là đối xứng 
	 m ij = m ji , 	  i , j. 
12 
Quan hệ hai ngôi 
3. Biểu diễn quan hệ 
+) R là phản xứng nếu M R thỏa: 
	m ij = 0 hoặc m ji = 0 nếu i ≠ j 
13 
Quan hệ hai ngôi 
1 . Định nghĩa. 
14 
Ví dụ: Cho S = {sinh viên của lớp}, gọi R là một quan hệ trên S với R = {( a,b ): a có cùng họ với b}. 
Quan hệ tương đương 
1. Định nghĩa : Quan hệ R trên tập A được gọi là tương đương nếu và chỉ nếu nó có tính chất phản xạ, đối xứng và bắc cầu. 
Ví dụ : Quan hệ R trên tập các chuỗi ký tự xác định bởi aRb nếu a và b có cùng độ dài. Khi đó R là quan hệ tương đương. 
Ví dụ: Cho R là quan hệ trên tập R sao cho 
	aRb a – b Z 
Khi đó R là quan hệ tương đương . 
15 
Quan hệ tương đương 
16 
Định nghĩa. 
Ví dụ : Cho m là số nguyên dương và R là q uan hệ trên Z : 
	 aRb ( a – b ) chia hết m 
K hi đó R là quan hệ t ương đương. 
- Rõ ràng quan hệ này có tính phản xạ và đối xứng. 
- Cho a , b , c sao cho a – b và b – c chia hết cho m , khi đó 
a – c = a – b + b – c cũng chia hết cho m . Suy ra R có tính 
chất bắc cầu. 
- Quan hệ này được gọi là đồng dư modulo m và chúng 
ta viết a  b (mod m ) thay vì aRb. 
Ví dụ: Cho | là q uan hệ trên Z được xác định như