Bài giảng Toán rời rạc - Chương 3: Phép đếm và hệ thức đệ quy

TOÁN RỜI RẠC - HK1 - NĂM 2015 -2016
Chương 3
PHÉP ĐẾM VÀ HỆ THỨC
ĐỆ QUY
lvluyen@hcmus.edu.vn
∼luyen/trr
FB: fb.com/trr2015
Trường Đại Học Khoa học Tự nhiên TP Hồ Chí Minhlvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 1/62
Nội dung
Chương 3.
PHÉP ĐẾM VÀ HỆ THỨC ĐỆ QUY
1. Các nguyên lý đếm cơ bản
2. Giải tích tổ hợp
3. Hoán vị lặp, tổ hợp lặp
4. Hệ thức đệ quy
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 2/62
3.1. Các nguyên lý đếm cơ bản
1 Nguyên lý cộng
2 Nguyên lý nhân
3 Nguyên lý bù trừ
4 Nguyên lý Derichlet
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 3/62
3.1.1. Nguyên lý cộng
Giả sử để làm công việc A ta có 2 phương pháp
Phương pháp 1: có n cách làm
Phương pháp 2: có m cách làm
Khi đó số cách làm công việc A là n+m.
Ví dụ. An có 3 áo tay dài, 5 áo tay ngắn. Để chọn một cái áo thì An
có mấy cách?
Đáp án. 3+5 =8 cách.
Ví dụ. Nhà trường cần chọn một sinh viên khoa CNTT năm hai, năm
ba hoặc năm tư đi tham gia hội nghị sinh viên thành phố. Biết rằng
trường có 501 sinh viên năm hai, 402 sinh viên năm ba, 345 sinh viên
năm tư. Hỏi có bao nhiêu cách chọn?
Đáp án. 501 + 402 + 345 = 1248 cách.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 4/62
3.1.2. Nguyên lý nhân
Giả sử để làm công việc A cần thực hiện 2 bước
Bước 1 có n cách làm
Bước 2 có m cách làm
Khi đó số cách làm công việc A là n×m.
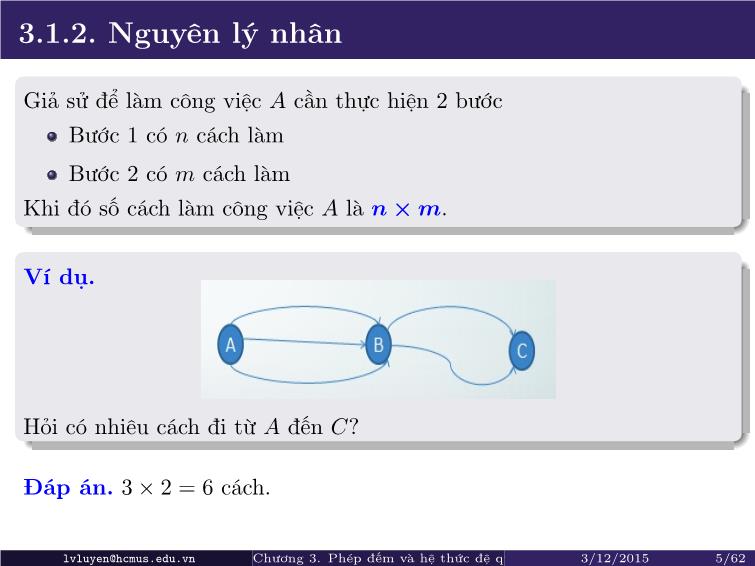
Ví dụ.
Hỏi có nhiêu cách đi từ A đến C?
Đáp án. 3× 2 = 6 cách.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 5/62
Ví dụ. Có bao nhiêu chuỗi bit có độ dài 8?
Giải. Mỗi bit có thể chọn 1 trong 2 cách: 0 hoặc 1. Theo nguyên lý
nhân ta có số lượng chuỗi là 28 = 256.
Ví dụ. Cho tập A gồm 6 phần tử và tập B gồm 10 phần tử. Hỏi
a) Có bao nhiêu ánh xạ từ A vào B?
b) Có bao nhiêu đơn ánh từ A vào B?
Giải. a) Với mỗi phần tử x của A ta có 10 cách chọn ảnh của x (vì B
có 10 phần tử). Theo nguyên lý nhân, ta có 106 ánh xạ.
b) Giải sử A = {x1, x2, . . . , x6}. Ta chia bài toán thành 6 bước:
Bước 1. Chọn ảnh của x1 có 10 cách.
Bước 2. Chọn ảnh của x2 có 10− 1 = 9 cách.
................
Bước 6. Chọn ảnh của x6 có 10− 5 = 5 cách.
Vậy số đơn ánh là: 10× 9× 8× 7× 6× 5 = 151200.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 6/62
Ví dụ. Cho tập X = {0, 1, 2, 3, 4, 5}. Hỏi có bao nhiêu số tự nhiên có
ba chữ số khác nhau mà chia hết cho 2?
Giải. Gọi số có ba chữ số là abc.
Trường hợp 1. c = 0. Khi đó
c có 1 cách chọn
a có 5 cách chọn ( a = X \ {0} )
b có 4 cách chọn ( b = X \ {a, 0} )
Trường hợp 1 có 1× 4× 5 = 20 số.
Trường hợp 2. c 6= 0. Khi đó
c có 2 cách chọn
a có 4 cách chọn ( a = X \ {c, 0} )
b có 4 cách chọn ( b = X \ {a, c} )
Trường hợp 2 có 2× 4× 4 = 32 số.
Như vậy có 20 + 32 = 52 số.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 7/62
3.1.3. Nguyên lý bù trừ
Ví dụ. Có bao nhiêu chuỗi bit có độ dài 8 hoặc được bắt đầu bằng 1
hoặc kết thúc bằng 00?
Cho A và B là hai tập hữu hạn. Khi đó
|A∪B| = |A|+ |B| − |A∩B|
Giải ví dụ trên.
Số lượng chuỗi bit bắt đầu bằng 1 là 27 = 128.
Số lượng chuỗi bit kết thúc bằng 00 là 26 = 64.
Số lượng chuỗi bit bắt đầu bằng 1 và kết thúc bằng 00 là 25 = 32.
Số lượng chuỗi bit thỏa đề bài là 128 + 64− 32 = 160.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 8/62
Ví dụ. Có 2 bài toán kiểm tra. Trong lớp có 30 sinh viên làm được bài
thứ nhất và 20 sinh viên làm được bài thứ hai và chỉ có 10 sinh viên
làm được cả 2 bài. Biết rằng mỗi sinh viên đều làm ít nhất một bài, hỏi
lớp có bao nhiêu sinh viên?
Giải. Ta gọi
A là những sinh viên giải được bài 1
B là những sinh viên giải được bài 2
Khi đó A ∩B là những sinh viên giải được cả 2 bài toán. Bài toán đặt
ra là tính số phần tử A ∪B. Ta có
|A ∪B| = |A|+ |B| − |A ∩B|
= 30 + 20− 10 = 40.
Như vậy lớp có 40 sinh viên.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 9/62
|A∪B ∪C| = |A|+ |B|+ |C| − |A∩B| − |B ∩C| − |A∩C|+ |A∩B ∩C|
Ví dụ.(tự làm) Bài kiểm tra Toán Rời Rạc có 3 bài. Biết rằng, mỗi
sinh viên làm được ít nhất 1 bài, trong đó có
20 sinh viên làm được bài 1.
14 sinh viên làm được bài 2.
10 sinh viên làm được bài 3.
6 sinh viên giải được bài 1 và 3.
5 sinh viên giải được bài 2 và bài 3.
2 sinh viên giải được bài 1 và 2.
1 sinh viên giải được cả 3 bài.
Hỏi lớp có bao nhiêu sinh viên?
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 10/62
3.1.4. Nguyên lý Derichlet (chuồng bồ câu)
Ví dụ.
Trong 1 nhóm có 367 người thì ít nhất có 2 người sinh cùng ngày.
Có 20 chim bồ câu ở trong 7 cái chuồng. Khi đó sẽ có ít nhất 1
chuồng có 3 con bồ câu trở lên.
Định nghĩa. Giá trị trần của x, ký hiệu là dxe, là số nguyên nhỏ
nhất mà lớn hơn hay bằng x.
Ví dụ. d2.1e = 3; d1.9e = 2; d4e = 4;
d−1.1e = −1. d−2.9e = −2; d−4e = −4.
Nguyên lý Derichlet
Giả sử có n chim bồ câu ở trong k chuồng. Khi đó tồn tại ít nhất một
chuồng chứa từ
⌈n
k
⌉
bồ câu trở lên.
 ... số cách đi hết cầu thang là xn−1.
Trường hợp 2. Bước đầu tiên gồm 2 bậc. Khi đó, cầu thang còn
n− 2 bậc nên số cách đi hết cầu thang trong là xn−2.
Theo nguyên lý cộng, số cách đi hết cầu thang là xn−1 + xn−2. Do đó
ta có:
xn = xn−1 + xn−2
Như vậy {
x1 = 1, x2 = 2;
xn = xn−1 + xn−2 với n > 2.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 36/62
3.4.2. Hệ thức đệ quy tuyến tính với hệ số hằng
Định nghĩa. Một hệ thức đệ quy tuyến tính cấp k với hệ số
hằng là một hệ thức có dạng:
a0xn+ a1xn−1+ . . .+ akxn−k = fn (1)
trong đó
a0 6= 0, a1, . . . , an là các hệ số thực;
{fn} là một dãy số thực cho trước và
{xn} là dãy ẩn nhận các giá trị thực.
Trường hợp dãy fn = 0 với mọi n thì (1) trở thành
a0xn+ a1xn−1+ . . .+ akxn−k = 0 (2)
Ta nói (2) là một hệ thức đệ quy tuyến tính thuần nhất cấp k
với hệ số hằng .
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 37/62
Ví dụ.
2xn − 5xn−1 + 2xn−2 = −n2 − 2n+ 3 −→ tuyến tính cấp 2.
xn − 3xn−1 + 2xn−3 = 20 + n2n−2 + 3n −→ tuyến tính cấp 3.
2xn+2 + 5xn+1 + 2xn = (35n+ 51)3
n −→ tuyến tính cấp 2.
xn+2 − 2xn+1 + xn = 0 −→ tuyến tính thuần nhất cấp 2.
Định nghĩa. Xét hệ thức đệ quy tuyến tính cấp k
a0xn+ a1xn−1+ . . .+ akxn−k = fn (1)
Mỗi dãy {xn} thỏa (1) được gọi là một nghiệm của (1).
Nhận xét rằng mỗi nghiệm {xn} của (1) được hoàn toàn xác định bởi
k giá trị ban đầu x0, x1, . . . , xk−1.
Họ dãy số {xn = xn(C1, C2, . . . , Ck)} phụ thuộc vào k họ tham số
C1, C2, . . . , Ck được gọi là nghiệm tổng quát của (1) nếu mọi dãy
của họ này đều là nghiệm của (1).
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 38/62
Với k giá trị ban đầu y0, y1, . . . , yk−1, tồn tại duy nhất các giá trị của k
tham số C1, C2, . . . , Ck sao cho nghiệm {xn} tương ứng thỏa
x0 = y0, x1 = y1, . . . , xk−1 = yk−1 (∗)
Khi đó, nghiệm {xn} tương ứng được gọi nghiệm riêng ứng với điều
kiện ban đầu (∗).
Giải một hệ thức đệ quy là đi tìm nghiệm tổng quát của nó; nhưng
nếu hệ thức đệ quy có kèm theo điều kiện ban đầu, ta phải tìm
nghiệm riêng thỏa điều kiện ban đầu đó.
Ví dụ.
2xn − 3xn−1 = 0 có nghiêm tổng quát là xn = C
(
3
2
)n

xn − 5xn−1 + 6xn−2 = 0;
x0 = 4;
x1 = 9.
có nghiệm riêng là xn = 3 · 2n + 3n.
Lưu ý. Trong phạm vi của chương trình ta chỉ xét các hệ thức đệ quy
tuyến tính (cấp 1 và 2) với hệ số hằng.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 39/62
3.4.3. Nghiệm của HTĐQTT thuần nhất
Xét hệ thức đệ quy tuyến tính thuần nhất
a0xn + a1xn−1 + . . .+ akxn−k = 0 (1)
Phương trình đặc trưng của (1) là phương trình bậc k định bởi:
a0λ
k + a1λ
k−1+ . . .+ ak = 0 (∗)
Trường hợp k = 1. Phương trình đặc trưng (∗) trở thành
a0λ+ a1 = 0
nên có nghiệm là
λ0 = −a1
a0
.
Khi đó, (1) có nghiệm tổng quát là: xn = C λn0 .
Trường hợp k = 2. Phương trình đặc trưng (∗) trở thành
a0λ
2+ a1λ+ a2 = 0 (∗)
Người ta chứng minh được kết quả sau:
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 40/62
Nếu (∗) có hai nghiệm thực phân biệt λ1 và λ2 thì (1) có nghiệm
tổng quát là:
xn = C1 λ
n
1 +C2 λ
n
2
Nếu (∗) có nghiệm kép thực λ0 thì (1) có nghiệm tổng quát là
xn = (C1+ nC2)λ
n
0
Nếu (∗) có hai nghiệm phức liên hợp được viết dưới dạng
λ = r(cosϕ± i sinϕ)
thì (1) có nghiệm tổng quát là
xn = r
n(A cosnϕ+B sinnϕ)
Ví dụ. Giải hệ thức đệ quy
{
xn − 2xn−1 = 0
x0 = 5.
(1)
Giải. Phương trình đặc trưng là λ− 2 = 0 có nghiệm là λ = 2. Suy ra
(1) có nghiệm tổng quát là xn = C2n.
Từ điều kiện x0 = 5 ta có C = 5. Suy ra nghiệm của (∗) là xn = 5 · 2n.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 41/62
Ví dụ. Tìm nghiệm của

xn = 5xn−1 − 6xn−2;
x0 = 4;
x1 = 9.
(2)
Giải. xn = 5xn−1 − 6xn−2
⇔ xn − 5xn−1 + 6xn−2 = 0
Phương trình đặc trưng
λ2− 5λ+ 6 = 0
có 2 nghiệm thực phân biệt λ1 = 2 và λ2 = 3. Suy ra (2) có nghiệm
tổng quát là
xn = C1 2
n+C2 3
n.
Vì x0 = 4; x1 = 9 nên
{
C1 + C2 = 4
2C1 + 3C2 = 9.
Suy ra C1 = 3, C2 = 1. Vậy
nghiệm của hệ thức đệ quy là
xn = 3 · 2n+ 3n.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 42/62
Ví dụ. Tìm nghiệm của

4xn+1 − 12xn + 9xn−1 = 0;
x0 = 2;
x1 = 9.
(3)
Giải. Phương trình đặc trưng
4λ2− 12λ+ 9 = 0
có 1 nghiệm thực kép là λ0 = 3/2 và λ2 = 3. Suy ra (3) có nghiệm tổng
quát là
xn = (C1 + nC2)
(
3
2
)n
.
Vì x0 = 2; x1 = 9 nên
{
C1 = 2
3
2
(C1 + C2) = 9.
Suy ra C1 = 2, C2 = 4. Vậy
nghiệm của hệ thức đệ quy là
xn = (2 + 4n)
(
3
2
)n
.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 43/62
Ví dụ. Tìm nghiệm của

xn+2 − 2xn+1 + 4xn = 0;
x0 = 1;
x1 = 4.
(4)
Giải. Phương trình đặc trưng λ2− 2λ+ 4 = 0 có 2 nghiệm phức liên
hợp là
λ = 1± i
√
3 = 2
(
cos
pi
3
± i sin pi
3
)
.
Suy ra (4) có nghiệm tổng quát là
xn = 2
n
(
A cos
npi
3
+B sin
npi
3
)
.
Vì x0 = 1; x1 = 4 nên

A = 1
2
(
1
2
A+
√
3
2
B
)
= 4.
Suy ra
A = 1, B =
√
3. Vậy nghiệm của hệ thức đệ quy là
xn = 2
n
(
A cos
npi
3
+
√
3 sin
npi
3
)
.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 44/62
3.4.4. Nghiệm của HTĐQTT không thuần nhất
Xét hệ thức đệ quy tuyến tính không thuần nhất
a0xn+ a1xn−1+ . . .+ akxn−k = fn (1)
Hệ thức đệ quy tuyến tính thuần nhất tương ứng là
a0xn+ a1xn−1+ . . .+ akxn−k = 0 (2)
Phương trình đặc trưng của (2) là:
a0λ
k + a1λ
k−1 + . . .+ ak = 0 (∗)
Khi đó
Để tìm một nghiệm riêng của (1), ta xem xét các dạng đặc biệt của vế
trái fn như sau:
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 45/62
Dạng 1. fn = βnPr(n), trong đó Pr(n) là một đa thức bậc r theo
n; β là một hằng số.
Dạng 2. fn = fn1 + fn2 + . . .+ fns , trong đó các fn1 , fn2 , . . . , fns
thuộc dạng 1.
Dạng 1. fn = βnPr(n). Có ba trường hợp xảy ra:
TH 1. Nếu β không là nghiệm của phương trình đặc trưng (∗) thì
(1) có một nghiệm riêng dạng:
xn = β
nQr(n)
TH 2. Nếu β là nghiệm đơn của phương trình đặc trưng (∗) thì
(1) có một nghiệm riêng dạng:
xn = nβ
nQr(n)
TH 3. Nếu β là nghiệm kép của phương trình đặc trưng (∗) thì
(1) có một nghiệm riêng dạng:
xn = n
2βnQr(n)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 46/62
Chú ý Qr(n) = Arnr +Ar−1nr−1+ . . .+A0 là đa thức có cùng
bậc r với Pr(n), trong đó Ar, Ar−1, . . . , A0 là r + 1 hệ số cần xác định.
Để xác định các hệ số trên ta cần thế xn, xn−1, . . . , xn−k vào (1) và cho
n nhận r+ 1 giá trị nguyên nào đó hoặc đồng nhất các hệ số tương ứng
ở hai vế để được một hệ phương trình. Các hệ số trên là nghiệm của hệ
phương trình này.
Dạng 2. fn = fn1 + fn2 + . . .+ fns . Bằng cách như trên ta tìm được
nghiệm riêng xni(1 ≤ i ≤ s) của hệ thức đệ quy
a0xn + a1xn−1 + . . .+ akxn−k = fni
Khi đó
xn = xn1 + xn2 + . . .+ xns
là một nghiệm riêng của (1).
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 47/62
Ví dụ. Cho hệ thức đệ quy
xn − 5xn−1 + 6xn−2 = fn (1).
Khi đó hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
xn− 5xn−1+ 6xn−2 = 0 (2)
Phương trình đặc trưng của (2) là:
λ2− 5λ+ 6 = 0 (∗)
có hai nghiệm thực là λ1 = 2 và λ2 = 3.
Nếu fn = 2n+ 1 thì (1) có nghiệm riêng dạng xn
(p)
= An+B.
Nếu fn = 5n(3n2 + 2n+ 1) thì xn
(p)
= 5n(An2 +Bn+ C).
Nếu fn = 5n, thì xn
(p)
= 5nA.
Nếu fn = 3n thì xn
(p)
= n3nA.
Nếu fn = 2n(3n+ 1) thì xn
(p)
= n2n(An+B).
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 48/62
Ví dụ. Cho hệ thức đệ quy
xn − 6xn−1 + 9xn−2 = fn (1).
Khi đó hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
xn− 6xn−1+ 9xn−2 = 0 (2)
Phương trình đặc trưng của (2) là:
λ2− 6λ+ 9 = 0 (∗)
có nghiệm kép là λ0 = 3.
Nếu fn = 3n thì (1) có nghiệm riêng dạng xn
(p)
= n23nA.
Nếu fn = 3n(5n+ 1) thì xn
(p)
= n23n(An+B).
Nếu fn = 2n(5n+ 1) thì xn
(p)
= 2n(An+B).
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 49/62
Ví dụ. Tìm nghiệm của
{
xn − 5xn−1 + 6xn−2 = 2n+ 1;
x0 = 1; x1 = 3.
Giải. Hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
xn− 5xn−1+ 6xn−2 = 0 (2)
Phương trình đặc trưng của (2) là:
λ2− 5λ+ 6 = 0 (∗)
có hai nghiệm thực là λ1 = 2 và λ2 = 3. Do đó nghiệm tổng quát của
(2) là:
xn = C1 2
n+C2 3
n (3)
Bây giờ ta tìm một nghiệm riêng của (1). Vế phải của (1) là
fn = 2n+ 1 có dạng βnPr(n) với β = 1 và Pr(n) là đa thức bậc r = 1.
Vì β = 1 không là nghiệm của phương trình đặc trưng (∗) nên (1) có
một nghiệm riêng dạng:
xn = an+ b (4)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 50/62
Thế (4) vào (1) ta được:
(an+ b)− 5[a(n− 1) + b] + 6[a(n− 2) + b] = 2n+ 1.
Cho n lần lượt nhận hai giá trị n = 0;n = 1 ta được hệ:{ −7a+ 2b = 1;
−5a+ 2b = 3.
Giải hệ trên ta được a = 1; b = 4. Thế vào (4) ta tìm được một nghiệm
riêng của (1) là:
xn = n+ 4 (5)
Từ (3) và (5) ta suy ra nghiệm tổng quát của (1) là:
xn = C1 2
n + C2 3
n + n+ 4
Thay điều kiện x0 = 1 và x1 = 3 vào (6) ta được{
C1 + C2 = −3
2C1 + 3C2 = −2.
Từ đó ta có C1 = −7 và C2 = 4. Thế vào (6) ta được
xn = −7 · 2n+ 4 · 3n+ n+ 4.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 51/62
Ví dụ. Giải hệ thức đệ quy
2xn − 3xn−1 + xn−2 = 4n+ 1. (1)
Giải. Hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
2xn− 3xn−1+ xn−2 = 0 (2)
Phương trình đặc trưng của (2) là:
2λ2− 3λ+ 1 = 0 (∗)
có hai nghiệm thực là λ1 = 1 và λ2 = 1/2. Do đó nghiệm tổng quát của
(2) là:
xn = C1 + C2
(
1
2
)n
Bây giờ ta tìm một nghiệm riêng của (1). Vế phải của (1) là
fn = 4n+ 1 có dạng βnPr(n) với β = 1 và Pr(n) là đa thức bậc r = 1.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 52/62
Vì β = 1 là nghiệm đơn của phương trình đặc trưng (∗) nên (1) có một
nghiệm riêng dạng:
xn = n(an+ b) (4)
Thế (4) vào (1) ta được:
2n(an+ b)− 3(n− 1)[a(n− 1) + b] + (n− 2)[a(n− 2) + b] = 4n+ 1.
Cho n lần lượt nhận hai giá trị n = 0;n = 1 ta được hệ:{
a+ b = 1;
3a+ b = 5.
Giải hệ trên ta được a = 2; b = −1. Thế vào (4) ta tìm được một
nghiệm riêng của (1) là:
xn = n(2n− 1) (5)
Từ (3) và (5) ta suy ra nghiệm tổng quát của (1) là:
xn = C1 + C2
(
1
2
)n
+ n(2n− 1)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 53/62
Ví dụ. Tìm nghiệm của
{
xn+1 − 6xn + 9xn−1 = (18n+ 12)3n;
x0 = 2; x1 = 0.
(1)
Giải. Hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
xn+1− 6xn+ 9xn−1 = 0 (2)
Phương trình đặc trưng của (2) là:
λ2− 6λ+ 9 = 0 (∗)
có nghiệm kép là λ0 = 3. Do đó nghiệm tổng quát của (2) là:
xn = (C1+ nC2)3
n (3)
Bây giờ ta tìm một nghiệm riêng của (1). Vế phải của (1) là
fn = (18n+ 12)3
n có dạng βnPr(n) với β = 3 và Pr(n) là đa thức bậc
r = 1.
Vì β = 3 là nghiệm kép của phương trình đặc trưng (∗) nên (1) có một
nghiệm riêng dạng:
xn = n
23n(an+ b) (4)
Thế (4) vào (1) ta được:
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 54/62
(n+ 1)23n+1[a(n+ 1) + b]− 6n23n(an+ b)+
9(n− 1)23n−1[a(n− 1) + b] = (18n+ 12)3n.
Cho n lần lượt nhận hai giá trị n = 0;n = 1 ta được hệ:{
6b = 12;
54a+ 18b = 90.
Giải hệ trên ta được a = 1; b = 2. Thế vào (4) ta tìm được một nghiệm
riêng của (1) là:
xn = n
2(n+ 2)3n (5)
Từ (3) và (5) ta suy ra nghiệm tổng quát của (1) là:
xn = (C1 + nC2)3
n + n2(n+ 2)3n (6)
Thay điều kiện x0 = 2 và x1 = 0 vào (6) ta được{
C1 = 2
3C1 + 3C2 + 9 = 0.
Từ đó ta có C1 = 2 và C2 = −5. Thế vào (6) ta được
xn = (2− 5n)3n + n2(n+ 2)3n = 3n(n3+ 2n2− 5n+ 2)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 55/62
Ví dụ. Tìm nghiệm của hệ thức đệ quy
xn − 4xn−1 + 3xn−2 = 20 + (2− n)2n−2 + 3 · 4n (1)
Giải. Hệ thức đệ quy tuyến tính thuần nhất tương ứng là:
xn− 4xn−1+ 3xn−2 = 0 (2)
Phương trình đặc trưng của (2) là:
λ2− 4λ+ 3 = 0 (∗)
có hai nghiệm thực là λ1 = 1 và λ2 = 3. Do đó nghiệm tổng quát của
(2) là:
xn = C1+C2 3
n (3)
Bây giờ ta tìm một nghiệm riêng của (1). Vế phải của (1) là
fn = 20 + (2− n)2n−2 + 3 · 4n thuộc Dạng 2. Ta xét các hệ thức đệ
quy sau:
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 56/62
xn − 4xn−1 + 3xn−2 = 20 (1a)
xn − 4xn−1 + 3xn−2 = (2− n)2n−2 (1b)
xn − 4xn−1 + 3xn−2 = 3 · 4n (1c)
Bằng cách giải tương tự như Dạng 1, ta có các nghiệm riêng của
(1a) là xn1 = −10n
(1b) là xn2 = n2
n
(1c) là xn3 = 4
n+2
Như vậy, (1) có nghiệm riêng là:
xn = −10n+ n2n+ 4n+2 (4)
Từ (3) và (4), ta suy ra nghiệm tổng quát của (1) là
xn = C1+C2 3
n− 10n+ n2n+ 4n+2
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 57/62
Ví dụ. Với n ≥ 1, đặt
sn =
n∑
k=1
k(k + 1)2k.
Tính tổng sn theo n bằng cách thiết lập một hệ thức đệ quy có điều
kiện đầu và tìm nghiệm của hệ thức đệ quy đó.
Đáp án.
{
sn − sn−1 = 2n(n2 + n)
s1 = 4.
; sn = −4 + 2n(2n2 − 2n+ 4)
Ví dụ. Cho x0 = 1 và x1 = 2. Tìm nghiệm của hệ thức đệ quy
xn+1 − 3xn + 2xn−1 = n, với n ≥ 1.
Đáp án. xn = 3 · 2n − 1
2
n2 − 3
2
n− 2
Ví dụ.(tự làm) Gọi xn là số chuỗi bit có chiều dài n mà không có 2 bit
0 đứng liền nhau. Hãy lập hệ thức đệ quy của xn và tìm xn.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 58/62
Ví dụ.(tự làm)
a) Tìm nghiệm tổng quát của hệ thức đệ quy:
an = 6an−1 − 9an−2.
b) Tìm một nghiệm riêng của hệ thức đệ quy sau
an = 6an−1 − 9an−2 + (18n− 6)3n−1.
c) Tìm nghiệm thỏa điều kiện đầu: a0 = 2, a1 = 9 của hệ thức đệ quy:
an = 6an−1 − 9an−2 + n3n+1.
Đáp án. a) xn = 3n(C1 + C2 · n) b) xn = n23n(n+ 2)
c) xn = 3n
(
1
2
n3 +
3
2
n2 − n+ 2
)
Ví dụ.(tự làm) Cho x0 = 1 và x1 = 6. Tìm nghiệm của hệ thức đệ quy
xn − 4xn−1 + 8xn−2 = 0, với n ≥ 2.
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 59/62
Đáp án. xn = (2
√
2)n
(
cos
npi
4
+ 2 sin
npi
4
)
Ví dụ.(tự làm)
a) Tìm nghiệm tổng quát của hệ thức đệ quy: xn − xn−1 − 2xn−2 = 0
b) Tìm nghiệm của hệ thức đệ quy: xn − xn−1 − 2xn−2 = (6n− 5)2n−1
thỏa điều kiện đầu x0 = 7, x1 = 4.
Đáp án. a) xn = C1 (−1)n + C2 2n b) xn = 4 · (−1)n + 2n(n2 + 3)
Ví dụ.(tự làm)
a) Tìm nghiệm tổng quát của hệ thức đệ quy: an = an−1 + 6an−2.
b) Tìm nghiệm thỏa điều kiện đầu a0 = 8, a1 = 5 của hệ thức đệ quy:
an = an−1 + 6an−2 + 10n(−2)n − 3(−2)n−1
Đáp án. a) an = C1 · (−2)n+ C2 · 3n
b) an = 7 · 3n + (−2)n(2n2 + 5n+ 1)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 60/62
Bài tập. Giải các hệ thức đệ quy sau
a)
{
xn + 4xn−1 − 5xn−2 = 12n+ 8;
x0 = 0, x1 = −5.
b)
{
2xn+2 + 5xn+1 + 2xn = (35n+ 51)3
n;
x0 = 3, x1 = 0.
c)
{
xn+2 − 2xn+1 + xn = 2;
x0 = 1, x1 = 0.
d)
{
2xn − 5xn−1 + 2xn−2 = −n2 − 2n+ 3;
x0 = 1, x1 = 3.
e)
{
xn+2 − 16xn+1 + 64xn = 128 · 8n;
x0 = 2, x1 = 32.
f)
{
xn+2 − 8xn+1 + 15xn = 2 · 5n+1;
x0 = −1, x1 = −2.
Xem đáp án ở slide kế tiếp
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 61/62
Đáp án.
a) xn = −5
3
+
5
3
(−5)n + n2 + 4n
b) xn = 2
(
−1
2
)n
+ (−2)n + 3nn
c) xn = n2 − 2n+ 1
d) xn = −3 · 2n + n2 + 4n+ 4
e) xn = 8n(n2 + n+ 2)
f) xn = 3n + 5n(n− 2)
lvluyen@hcmus.edu.vn Chương 3. Phép đếm và hệ thức đệ quy 3/12/2015 62/62