Bài giảng Toán rời rạc - Chương 2: Tập hợp và ánh xạ

TOÁN RỜI RẠC - HK1 - NĂM 2015 -2016
Chương 2
TẬP HỢP VÀ ÁNH XẠ
lvluyen@hcmus.edu.vn
∼luyen/trr
FB: fb.com/trr2015
Trường Đại Học Khoa học Tự nhiên TP Hồ Chí Minh
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 1/33
Nội dung
Chương 2. TẬP HỢP VÀ ÁNH XẠ
1. Tập hợp
2. Ánh xạ
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 2/33
2.1. Tập hợp
1 Khái niệm
2 Các phép toán trên tập hợp
3 Tập các tập con của một tập hợp
4 Tích Descartes
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 3/33
2.1.1. Khái niệm
Tập hợp là một khái niệm cơ bản của Toán
học, dùng để chỉ một nhóm các đối tượng nào
đó mà chúng ta quan tâm.
Khi phần tử x thuộc tập hợp A ta ký hiệu
x ∈ A, ngược lại ta ký hiệu x /∈ A.
Ví dụ.
- Tập hợp sinh viên của một trường đại học.
- Tập hợp các số nguyên.
- Tập hợp các trái táo trên một cây.
Để minh họa tập hợp thì chúng ta dùng sơ đồ
Ven
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 4/33
Lực lượng của tập hợp
Số phần tử của tập hợp A được gọi là lực lượng của tập hợp, kí hiệu
|A|. Nếu A có hữu hạn phần tử, ta nói A hữu hạn. Ngược lại, ta nói A
vô hạn.
Ví dụ.
• |∅| = 0
• N,Z,Q,R, là các tập vô hạn
• X = {1, 3, 4, 5} là tập hữu hạn với |X| = 4
Cách xác định tập hợp
Có 2 cách:
1 Liệt kê tất cả các phần tử của tập hợp
A = {1, 2, 3, 4, a, b}
2 Đưa ra tính chất đặc trưng
B = {n ∈ N |n chia hết cho 3}
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 5/33
Quan hệ giữa các tập hợp
a. Bao hàm. Nếu mọi phần tử của tập hợp A đều là phần tử của tập
hợp B thì tập hợp A được gọi là tập hợp con của tập hợp B, ký hiệu là
A ⊂ B, nghĩa là
A ⊂ B⇔ ∀x,x ∈ A→ x ∈ B
b. Bằng nhau. Hai tập hợp A và B được gọi là bằng nhau nếu A ⊂ B
và B ⊂ A, ký hiệu A = B.
Ví dụ. Cho A = {1, 3, 4, 5}, B = {1, 2, 3, 4, 5, 6, 7, 8} và
C = {x ∈ Z | 0 < x < 9}. Khi đó
A ⊂ B và B = C.
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 6/33
2.1.2. Các phép toán trên tập hợp
a) Hợp
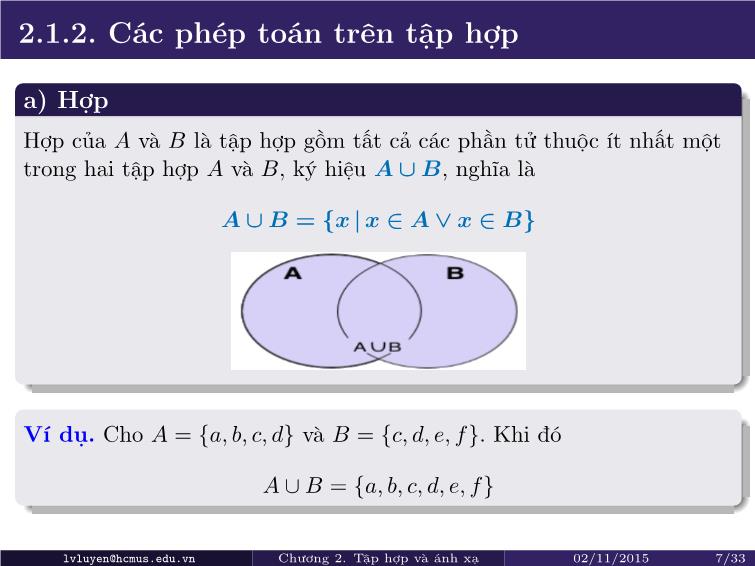
Hợp của A và B là tập hợp gồm tất cả các phần tử thuộc ít nhất một
trong hai tập hợp A và B, ký hiệu A∪B, nghĩa là
A∪B = {x |x ∈ A∨ x ∈ B}
Ví dụ. Cho A = {a, b, c, d} và B = {c, d, e, f}. Khi đó
A ∪B = {a, b, c, d, e, f}
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 7/33
Nhận xét. x ∈ A ∪B ⇔
[
x ∈ A
x ∈ B x /∈ A ∪B ⇔
{
x /∈ A
x /∈ B
Tính chất.
1 Tính lũy đẳng A ∪A = A
2 Tính giao hoán A ∪B = B ∪A
3 Tính kết hợp (A ∪B) ∪ C = A ∪ (B ∪ C)
4 Hợp với tập rỗng A ∪ ∅ = A
b) Giao
Giao của A và B là tập hợp gồm tất cả các phần tử vừa thuộc A và
thuộc B, ký hiệu A∩B, nghĩa là
A∩B = {x |x ∈ A∧ x ∈ B}
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 8/33
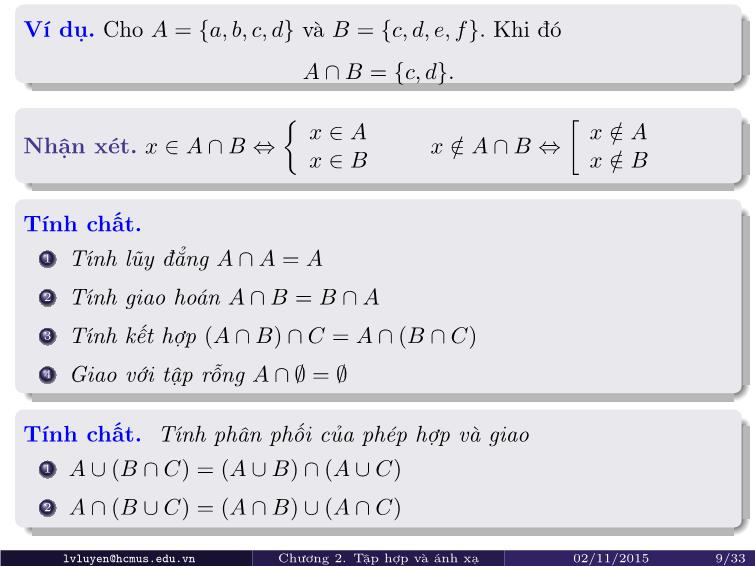
Ví dụ. Cho A = {a, b, c, d} và B = {c, d, e, f}. Khi đó
A ∩B = {c, d}.
Nhận xét. x ∈ A ∩B ⇔
{
x ∈ A
x ∈ B x /∈ A ∩B ⇔
[
x /∈ A
x /∈ B
Tính chất.
1 Tính lũy đẳng A ∩A = A
2 Tính giao hoán A ∩B = B ∩A
3 Tính kết hợp (A ∩B) ∩ C = A ∩ (B ∩ C)
4 Giao với tập rỗng A ∩ ∅ = ∅
Tính chất. Tính phân phối của phép hợp và giao
1 A ∪ (B ∩ C) = (A ∪B) ∩ (A ∪ C)
2 A ∩ (B ∪ C) = (A ∩B) ∪ (A ∩ C)
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 9/33
c) Hiệu
Hiệu của hai tập hợp A và B là tập hợp tạo bởi tất cả các phần tử
thuộc tập A mà không thuộc tập B ký hiệu A\B, nghĩa là
A\B = {x |x ∈ A∧ x /∈ B}
Nhận xét. x ∈ A\B ⇔
{
x ∈ A
x /∈ B x /∈ A\B ⇔
[
x /∈ A
x ∈ B
Tính chất. Cho A,B,C là các tập hợp. Khi đó
1 A\(B ∩ C) = (A\B) ∪ (A\C);
2 A\(B ∪ C) = (A\B) ∩ (A\C).
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 10/33
d) Tập bù
Khi A ⊂ U thì U\A gọi là tập bù của A trong U . Ký hiệu CUA hay
đơn giản là A
Ví dụ. Cho A = {1, 3, 4, 6} và U = {1, 2, 3, 4, 5, 6, 7, 8}. Khi đó
A = {2, 5, 7, 8}
Tính chất. Luật De Morgan
1 A ∩B = A ∪B
2 A ∪B = A ∩B
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 11/33
Tính chất.
A\B = A ∩B (triệt hiệu)
A ∩A = ∅.
Ví dụ. Cho A,B,C là các tập hợp. Chứng minh rằng:
a) A\(A\B) = A ∩B
b) A ∩ (B\C) = (A ∩B)\(A ∩ C)
c) (A\B) ∪ (A\C) = A\(B ∩ C)
d) (A\B) ∪ (B\A) = (A ∪B)\(A ∩B)
e) A ∩ (B\A) = ∅
f) A\B = A\(A ∩B) = (A ∪B)\B
Ví dụ. Cho các tập hợp A,B và C chứa trong E. Chứng minh
(B\C)\(B\A) = (A ∩B)\C.
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 12/33
Giải. VT = (B\C)\(B\A)
= (B ∩ C)\(B ∩A) (triệt hiệu)
= (B ∩ C) ∩ (B ∩A) (triệt hiệu)
= (B ∩ C) ∩ (B ∪A) (De Morgan)
= C ∩ (B ∩ (B ∪A)) (kết hợp)
= C ∩ ((B ∩B) ∪ (B ∩A)) (phân phối)
= C ∩ (∅ ∪ (B ∩A)) (bù)
= C ∩ (B ∩A) (trung hòa)
= (A ∩B) ∩ C (giao hoán, kết hợp)
= (A ∩B)\C = VP (triệt hiệu)
Ví dụ.(tự làm) Cho các tập hợp A, B và C ⊂ E. Chứng minh
A ∩ (B\C) = (A ∩B)\(A ∩ C).
lvluyen@hcmus.edu.vn Chương 2. Tập hợp và ánh xạ 02/11/2015 13/33
2.1.3. Tập các tập con của một tập hợp
Định nghĩa. Cho X là một tập hợp. Khi đó tập tất cả các tập con
của X được ký hiệu là P (X).
Ví dụ. Cho X = {a, b}. Khi đó
P (X) = {∅,{a},{b},{a, b}}
Ví dụ.(tự làm) Cho X = {1, 2, 3}. Tìm tập P (X)?
Câu hỏi. Nếu tập X có n