Bài giảng Toán A2 - Chương 1: Ma trận, định thức

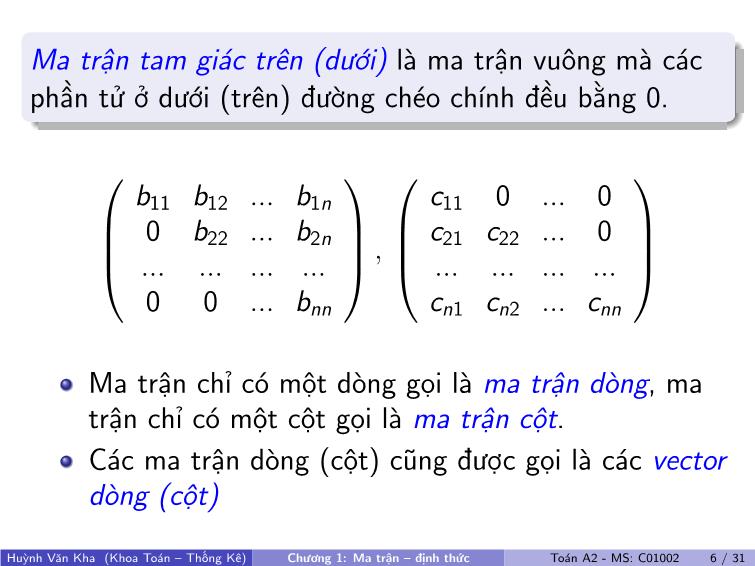
Chương 1
MA TRẬN - ĐỊNH THỨC
Huỳnh Văn Kha
Đại Học Tôn Đức Thắng
Toán A2 - MS: C01002
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 1 / 31
Nội dung
1 Định nghĩa, phân loại ma trận
2 Các phép toán trên ma trận
3 Chuyển vị ma trận, ma trận đối xứng
4 Phép biến đổi sơ cấp trên dòng (cột), đưa ma trận về
dạng bậc thang
5 Định thức của ma trận vuông
6 Ma trận nghịch đảo
7 Giải phương trình ma trận
8 Hạng của ma trận
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 1 / 31
Định nghĩa ma trận
Định nghĩa
Một ma trận cấp m × n là một bảng hình chữ nhật gồm
m hàng và n cột:
A =

a11 a12 · · · a1n
a21 a22 · · · a2n
· · · · · · · · · · · ·
am1 am2 · · · amn

Ký hiệu: A = (aij).
Phần tử dòng i , cột j của ma trận A được viết là: [A]ij
Tập các ma trận cấp m × n được ký hiệu:Mm×n
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 2 / 31
Ví dụ
A =
 1 3 −2 40 −3 10 8
4 5 1 0

Thì: [A]23 = 10, và A ∈M3×4
Ma trận bằng nhau
Hai ma trận gọi là bằng nhau nếu nó cùng kích
thước và các phần tử tương ứng bằng nhau.
Ví dụ: Tìm a, b, c để A = B , biết:
A =
 1 a0 −3
4 5
 và B =
 1 3b −3
4 c

Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 3 / 31
Phân loại ma trận
Ma trận không là ma trận mà mọi phần tử của nó đều
bằng 0. Ký hiệu: 0m×n, hoặc: 0.
Ma trận vuông cấp n là ma trận có số dòng và số cột
đều bằng n.
Tập các ma trận vuông cấp n được ký hiệu là:Mn
Các phần tử [A]11, [A]22, · · · , [A]nn gọi là nằm trên
đường chéo chính của ma trận vuông A.
Ví dụ: 02×3 =
(
0 0 0
0 0 0
)
, A =
 1 −2 30 6 5
2 3 −5

Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 4 / 31
Ma trận đường chéo cấp n là ma trận vuông cấp n mà
mọi phần tử bên ngoài đường chéo chính đều bằng 0.
Ma trận đơn vị cấp n là ma trận đường chéo cấp n mà
mọi phần tử trên đường chéo chính đều bằng 1.
Ký hiệu: In.
Ví dụ: A =
 3 0 00 −2 0
0 0 0

I2 =
(
1 0
0 1
)
, I3 =
 1 0 00 1 0
0 0 1

Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 5 / 31
Ma trận tam giác trên (dưới) là ma trận vuông mà các
phần tử ở dưới (trên) đường chéo chính đều bằng 0.

b11 b12 ... b1n
0 b22 ... b2n
... ... ... ...
0 0 ... bnn
 ,

c11 0 ... 0
c21 c22 ... 0
... ... ... ...
cn1 cn2 ... cnn

Ma trận chỉ có một dòng gọi là ma trận dòng, ma
trận chỉ có một cột gọi là ma trận cột.
Các ma trận dòng (cột) cũng được gọi là các vector
dòng (cột)
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 6 / 31
Cộng ma trận, nhân số với ma trận
Cho A,B ∈Mm×n và h ∈ R
Tổng của hai ma trận A và B là ma trận cấp m× n có ký
hiệu là A+B, được xác định bởi: [A+B]ij = [A]ij + [B]ij
Tích của ma trận A với hằng số h là ma trận cấp m × n
có ký hiệu là hA, được xác định bởi [hA]ij = h[A]ij
Ngoài ra, ta định nghĩa: A− B = A+ (−1)B
Ví dụ: cho A =
(
1 2 3
4 5 6
)
, B =
(
1 2 1
−1 1 3
)
.
Tính: A+ B , 2B , A− B , 2A− 3B
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 7 / 31
Tính chất
Với mọi ma trận A,B ,C ∈Mm×n và h, k ∈ R, ta có:
(i) A+ B = B + A (tính giao hoán)
(ii) (A+ B) + C = A+ (B + C ) (tính kết hợp)
(iii) A+ 0 = A (0: ma trận không cấp m × n)
(iv) A+ (−A) = 0
(v) h(kA) = (hk)A
(vi) h(A+ B) = hA+ hB
(vii) (h + k)A = hA+ kA
(viii) 1.A = A
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 8 / 31
Nhân hai ma trận
Cho A ∈Mm×n, B ∈Mn×p. Ta có định nghĩa sau.
Tích ma trận của A với B là ma trận cấp m × p, ký hiệu
là AB , xác định bởi:
[AB]ik =
n∑
j=1
[A]ij [B]jk = [A]i1[B]1k + · · ·+ [A]in[B]nk
với mọi i = 1,m, k = 1, p
Ví dụ: Tính AB , AC , CA, biết:
A=
 −2 1 11 1 3
−1 0 0
, B=
 1 20 1
1 −1
, C =
 0 2 −31 2 0
3 0 −4

Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 9 / 31
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 10 / 31
Tính chất
(i) (Tính kết hợp ) Với A ∈Mm×n, B ∈Mn×p và
C ∈Mp×q, ta có:
(AB)C = A(BC )
(ii) (Tính phân bố) Với A,B ∈Mm×n và C ∈Mn×p,
ta có:
(A+ B)C = AC + BC
Với C ∈Mm×n và A,B ∈Mn×p, ta có:
C (A+ B) = CA+ CB
(iii) Với mọi A ∈Mm×n, B ∈Mn×p và h ∈ R, ta có:
h(AB) = (hA)B = A(hB)
(iv) AIn = InA = A, với mọi A ∈Mn
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trận – định thức Toán A2 - MS: C01002 11 / 31
Ma trận chuyển vị, đối xứng
Cho A ∈Mm×n, chuyển vị của A, ký hiệu A>, là ma
trận cấp n ×m xác định bởi [A>]
ij
= [A]ji
Ví dụ: Tìm chuyển vị của A =
(
1 2 3
4 5 6
)
∈M2×3.
Tính chất:(
A>
)>
= A
(A+ B)> = A> + B>
(AB)> = B>A>
Ma trận vuông A gọi là đối xứng nếu A> = A
Huỳnh Văn Kha (Khoa Toán – Thống Kê) Chương 1: Ma trậ