Bài giảng Tài chính doanh nghiệp - Chương 3: Lợi nhuận và rủi ro - Bùi Ngọc Mai Phương

Th.S Bùi Ngọc Mai Phương 11/13/19
1
LOGO
1
Th.S Bùi Ngọc Mai Phương
1
CHƯƠNG 3: LỢI NHUẬN VÀ RỦI RO
2
3.1. Đo lường lợi nhuận và tỷ suất lợi nhuận
3.2. Rủi ro và suất sinh lời kỳ vọng
3.3. Mô hình định giá tài sản vốn (CAPM)
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
2
MỤC TIÊU CHƯƠNG 3
Sinh viên hiểu, biết được:
• Phương pháp đo lường lợi nhuận, rủi ro của
một khoản đầu tư và DMĐT
• Phân loại rủi ro
• Phân tích mối quan hệ giữa lợi nhuận và rủi ro
• Phân tích mô hình định giá tài sản vốn CAPM
3
3
3.1. Đo lường lợi nhuận và tỷ suất lợi nhuận
3.1.1. Lợi nhuận và tỷ suất sinh lời
3.1.2. Tỷ suất sinh lời trung bình (!R - Average Rate
of Return)
4
4
Th.S Bùi Ngọc Mai Phương 11/13/19
2
3.1.1. Lợi nhuận và tỷ suất sinh lời
Lợi nhuận là mức sinh lời của khoản đầu tư, được tính
bằng giá trị tăng thêm mà khoản đầu tư tạo ra trong khoảng
thời gian nhất định.
Tỷ suất sinh lời là tỷ lệ phần trăm giữa mức sinh lời mà
khoản đầu tư mang lại so với giá trị vốn gốc đầu tư ban đầu
trong cùng đơn vị thời gian.
5
3.1. Đo lường lợi nhuận và tỷ suất lợi nhuận
5
3.1.2. Tỷ suất sinh lời trung bình
Phản ánh khả năng đem lại lợi nhuận trung bình một kỳ (một
năm) cho nhà đầu tư trong thời gian nghiên cứu.
R = (R1"R2" "Rn)n = 1n ×
R = n 1+R1 × 1+R2  1+Rn - 1 
n số kỳ
Rn tỷ suất sinh lời mỗi kỳ
6
%
i = 1
n
Ri
3.1. Đo lường lợi nhuận và tỷ suất lợi nhuận
6
3.1.2. Tỷ suất sinh lời trung bình
Cổ phiếu A có các thông tin sau:
Tỷ suất sinh lời trung bình của cổ phiếu A?
7
Năm Tỷ suất sinh lời
1 5%
2 10%
3 15%
3.1. Đo lường lợi nhuận và tỷ suất lợi nhuận
7
3.2.1. Rủi ro
3.2.2. Đo lường rủi ro
3.2.3. Phân loại rủi ro
3.2.4. Mối quan hệ giữa lợi nhuận và rủi ro
8
3.2. Rủi ro và suất sinh lời kỳ vọng
8
Th.S Bùi Ngọc Mai Phương 11/13/19
3
3.2.1. Rủi ro
- Rủi ro là sự không chắc chắn, khả năng xuất
hiện các sự kiện không mong đợi sẽ xảy ra.
- Rủi ro là sự sai biệt giữa tỷ suất sinh lời thực tế
và tỷ suất sinh lời kỳ vọng
- Đo lường rủi ro: độ lệch chuẩn hoặc phương sai
9
3.2. Rủi ro và suất sinh lời kỳ vọng
9
3.2.2. Đo lường rủi ro
Tỷ suất sinh lời kỳ vọng (&R hay E(R) - Expected
Rate of Return) là tỷ suất sinh lời dự kiến xảy ra của
một khoản đầu tư.
Có 2 cách xác định:
§ Dựa vào dữ liệu dự báo xác suất
§ Dựa vào dữ liệu quá khứ
10
3.2. Rủi ro và suất sinh lời kỳ vọng
10
3.2.2. Đo lường rủi ro
- Xác định &R dựa vào dữ liệu dự báo xác suất
Ví dụ: xác định &RA năm 2018, biết phân phối xác suất
tỷ suất sinh lời của cổ phiếu A như sau:
11
Tình trạng nền kinh tế Ri(A) Pi
Suy thoái 5% 0,2
Trung bình 10% 0,5
Hưng thịnh 15% 0,3
3.2. Rủi ro và suất sinh lời kỳ vọng
11
3.2.2. Đo lường rủi ro
- Xác định &R dựa vào dữ liệu dự báo xác suất
Ri: TSSL ứng với biến cố thứ i
Pi: xác suất xảy ra biến cố thứ i và
n: số biến cố có thể xảy ra.
12
&R = %
i = 1
n
%
i = 1
n
Pi = 1
3.2. Rủi ro và suất sinh lời kỳ vọng
12
Th.S Bùi Ngọc Mai Phương 11/13/19
4
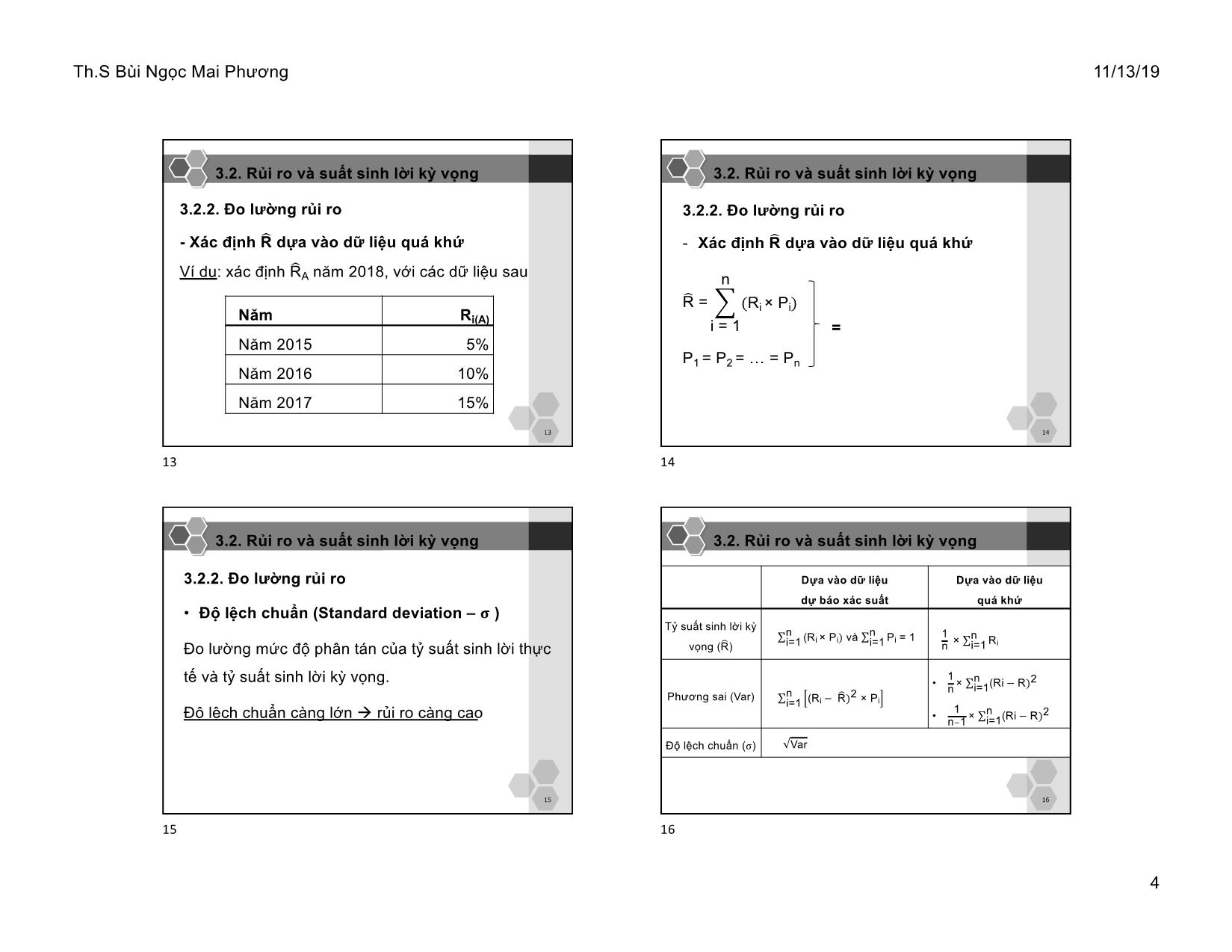
3.2.2. Đo lường rủi ro
- Xác định &R dựa vào dữ liệu quá khứ
Ví dụ: xác định &RA năm 2018, với các dữ liệu sau
13
Năm Ri(A)
Năm 2015 5%
Năm 2016 10%
Năm 2017 15%
3.2. Rủi ro và suất sinh lời kỳ vọng
13
3.2.2. Đo lường rủi ro
- Xác định &R dựa vào dữ liệu quá khứ
&R =
P1 = P2 =  = Pn
14
%
i = 1
n (Ri × Pi)
3.2. Rủi ro và suất sinh lời kỳ vọng
=
14
3.2.2. Đo lường rủi ro
• Độ lệch chuẩn (Standard deviation – 𝛔 )
Đo lường mức độ phân tán của tỷ suất sinh lời thực
tế và tỷ suất sinh lời kỳ vọng.
Độ lệch chuẩn càng lớn à rủi ro càng cao
15
3.2. Rủi ro và suất sinh lời kỳ vọng
15
Dựa vào dữ liệu
dự báo xác suất
Dựa vào dữ liệu
quá khứ 
Tỷ suất sinh lời kỳ
vọng (&R) ∑i=1n (Ri × Pi) và ∑i=1n Pi = 1 1n × ∑i=1n Ri
Phương sai (Var) ∑i=1n (Ri − &R)2 × Pi • 1n × ∑i=1n (Ri − R)2
• 1n,1 × ∑i=1n (Ri − R)2
Độ lệch chuẩn (σ) Var
16
3.2. Rủi ro và suất sinh lời kỳ vọng
16
Th.S Bùi Ngọc Mai Phương 11/13/19
5
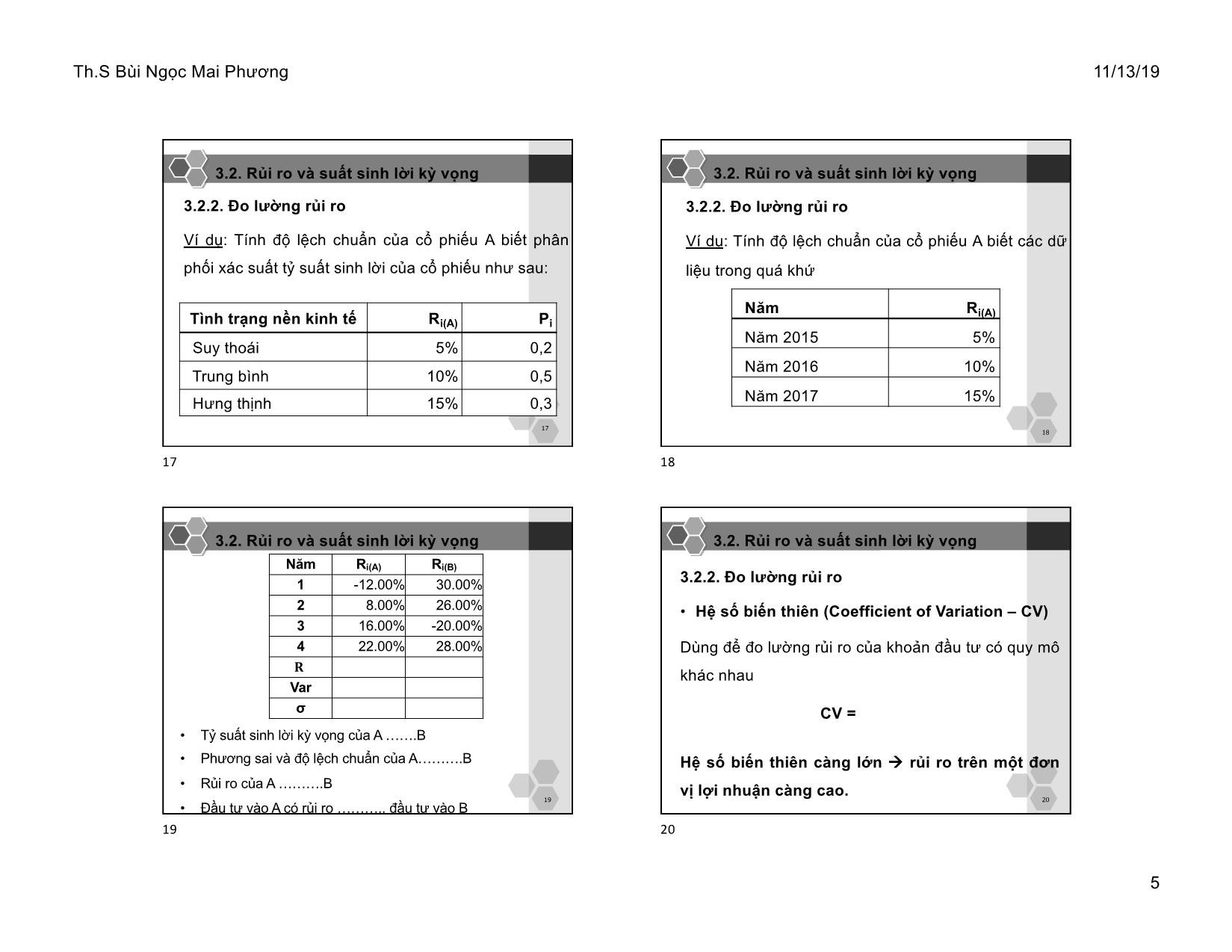
3.2.2. Đo lường rủi ro
Ví dụ: Tính độ lệch chuẩn của cổ phiếu A biết phân
phối xác suất tỷ suất sinh lời của cổ phiếu như sau:
17
Tình trạng nền kinh tế Ri(A) Pi
Suy thoái 5% 0,2
Trung bình 10% 0,5
Hưng thịnh 15% 0,3
3.2. Rủi ro và suất sinh lời kỳ vọng
17
3.2.2. Đo lường rủi ro
Ví dụ: Tính độ lệch chuẩn của cổ phiếu A biết các dữ
liệu trong quá khứ
18
Năm Ri(A)
Năm 2015 5%
Năm 2016 10%
Năm 2017 15%
3.2. Rủi ro và suất sinh lời kỳ vọng
18
19
3.2. Rủi ro và suất sinh lời kỳ vọng
Năm Ri(A) Ri(B)
1 -12.00% 30.00%
2 8.00% 26.00%
3 16.00% -20.00%
4 22.00% 28.00%𝐑
Var
σ 
• Tỷ suất sinh lời kỳ vọng của A .B
• Phương sai và độ lệch chuẩn của A.B
• Rủi ro của A .B
• Đầu tư vào A có rủi ro .. đầu tư vào B
19
3.2.2. Đo lường rủi ro
• Hệ số biến thiên (Coefficient of Variation – CV)
Dùng để đo lường rủi ro của khoản đầu tư có quy mô
khác nhau
Hệ số biến thiên càng lớn à rủi ro trên một đơn
vị lợi nhuận càng cao.
20
CV = 
3.2. Rủi ro và suất sinh lời kỳ vọng
20
Th.S Bùi Ngọc Mai Phương 11/13/19
6
3.2.3. Mối quan hệ giữa lợi nhuận và rủi ro
Lợi nhuận và rủi ro là hai mục tiêu mà nhà đầu tư
khi ra quyết định phải lựa chọn trên nguyên tắc
đánh đổi.
21
3.2. Rủi ro và suất sinh lời kỳ vọng
21
3.2.3. Mối quan hệ giữa lợi nhuận và rủi ro
- Nhà đầu tư thường không thích rủi ro à đầu tư
vào lĩnh vực có rủi ro thấp à tỷ suất sinh lời thấp.
- Nhà đầu tư thích rủi ro cao à đầu tư vào lĩnh
vực có rủi ro cao à tỷ suất sinh lời cao à nhận
phần bù rủi ro (Risk Premium – RP) của khoản
đầu tư.
22
3.2. Rủi ro và suất sinh lời kỳ vọng
22
3.2.3. Mối quan hệ giữa lợi nhuận và rủi ro
Khoản đầu tư có rủi ro ..à phần bù rủi ro
....à tỷ suất sinh lời yêu cầu .
Phần bù rủi ro là phần bù rủi ro hệ thống?
23
= +
3.2. Rủi ro và suất sinh lời kỳ vọng
23
3.2.3. Mối quan hệ giữa lợi nhuận và rủi ro
Ví dụ: Xem xét các cơ hội đầu tư
24
3.2. Rủi ro và suất sinh lời kỳ vọng
Cơ hội đầu tư
Tín phiếu
Chính phủ
Dự án A!R 7% 8,5%
σ 0 14,82%
Risk Premium
24
Th.S Bùi Ngọc Mai Phương 11/13/19
7
Hệ số Beta (𝛃)
Rủi ro hệ thống của một cổ phiếu được xác định bằng cách so
sánh biến động của cổ phiếu đó với biến động của TSSL thị
trường và được đo bằng hệ số Beta
Ví dụ: 𝛃A = 0,5𝛃B = 1,5
25
3.3. Mô hình định giá tài sản vốn CAPM
25
Hệ số Betaβ đo lường chính xác rủi ro hệ thống của cổ phiếu trong 1
DMĐT.β đo lường mức độ đóng góp của cổ phiếu vào rủi ro DMĐT
Cov(Ri,Rm): đồng phương sai TSSL của khoản đầu tư i với
TSSL thị trường.Var56 : phương sai của TSSL thị trường. 26
3.3. Mô hình định giá tài sản vốn CAPM
𝛃i = 𝐂𝐨𝐯(𝐑𝐢, 𝐑𝐦)𝐕𝐚𝐫𝐑𝐦
26
Capital asset pricing model - CAPM
Giả định:
• Thị trường vốn là thị trường hiệu quả và hoàn hảo
• Các NĐT có thể vay nợ và cho vay với lãi suất như nhau
và không thay đổi
• Không có thuế và chi phí giao dịch
• Tất cả các nhà đầu tư đều có kỳ vọng thuần nhất
27
3.3. Mô hình định giá tài sản vốn CAPM
27
Nội dung:
Mô hình CAPM mô tả mối quan hệ giữa rủi ro và lợi nhuận
• RA : TSSL kỳ vọng của A
• Rf : lãi suất phi rủi ro (lãi suất kỳ phiếu kho bạc 1 năm)
• Rm : TSSL kỳ vọng của DMĐT thị trường
• βA: hệ số beta đo lường rủi ro hệ thống của A
• Rm - Rf : phần bù rủi ro hệ thống của DMĐT thị trường
• (Rm - Rf) × βA: phần bù rủi ro hệ thống của A
28
3.4. Mô hình định giá tài sản vốn CAPM
RA = Rf + (Rm ˗ Rf) x 𝛃A
28
Th.S Bùi Ngọc Mai Phương 11/13/19
8
Ý nghĩa mô hình CAPM:
• Hệ số βA > 1à RR hệ thống của A  RR hệ thống DMĐT
• Hệ số βA = 1à RR hệ thống của A  RR hệ thống DMĐT
• Hệ số βA < 1à RR hệ thống của A  RR hệ thống DMĐT
29
3.3. Mô hình định giá tài sản vốn CAPM
29
Ví dụ:
• Lãi suất kỳ phiếu chính phủ kỳ hạn 1 năm là 10%.
• Lãi suất thị trường là 15%.
• Hệ số beta của chứng khoán A là 1,6.
Xác định TSSL của chứng khoán A ?
30
3.3. Mô hình định giá tài sản vốn CAPM
30
Ưu điểm
• Đơn giản và có thể ứng dụng trên thực tế ở nhiều
loại hình doanh nghiệp.
• Khi có đủ các thông số rm, rf, mô hình CAPM có thể
áp dụng cho mọi trường hợp cần tìm TSSL yêu cầu.
• Tỷ suất sinh lời yêu cầu được điều chỉnh theo rủi ro
của lĩnh vực đầu tư, thể hiện qua phần bù rủi ro.
31
3.3. Mô hình định giá tài sản vốn CAPM
31
Hạn chế:
• Nhiều giả định không tồn tại trong thực tế.
• Tồn tại nhiều quan điểm khác nhau trong việc
chọn lãi suất của tài sản phi rủi ro và hệ số Beta.
• Không quan tâm đến giá thị trường của chứng
khoán.
32
3.3. Mô hình định giá tài sản vốn CAPM
32
Th.S Bùi Ngọc Mai Phương 11/13/19
9
Hạn chế:
- Các nhà đầu tư không hoàn toàn bỏ qua rủi ro phi
hệ thống.
- Nếu nhà đầu tư không đa dạng hóa DMĐT, họ
phải gánh chịu toàn bộ rủi ro, trong khi mô hình
CAPM chỉ tính đến rủi ro thị trường của chứng
khoán.
- Vì vậy mô hình CAPM sẽ phản ánh lãi suất yêu
cầu của nhà đầu tư thấp hơn thực tế. 33
3.3. Mô hình định giá tài sản vốn CAPM
33
Phân loại rủi ro
• Rủi ro hệ thống (Unsystematic Risk)
• Rủi ro phi hệ thống (Systematic Risk)
34
34
Phân loại rủi ro
• Rủi ro hệ thống (Systematic Risk) – rủi ro thị
trường
- Là rủi ro xảy ra với tất cả các công ty
- Ảnh hưởng đến tất cả các khoản đầu tư trên thị
trường.
- Nguyên nhân: tình hình kinh tế, chính trị của đất
nước
35
35
Phân loại rủi ro
• Rủi ro phi hệ thống (Unsystematic Risk)
- Là rủi ro chỉ tác động lên một khoản đầu tư hay
một lĩnh vực đầu tư.
- Làm giảm tỷ suất sinh lời kỳ vọng lên một khoản
đầu tư hay một lĩnh vực đầu tư.
- Nguyên nhân: tính chất nội bộ của một công ty
hoặc một ngành nghề kinh doanh.
36
36
Th.S Bùi Ngọc Mai Phương 11/13/19
10
Phân loại rủi ro
? Nhà đầu tư có thể giảm thiểu rủi ro không
? Rủi ro được giảm thiểu bằng cách nào
37
37
Lãi suất thị trường (Rm) chỉ tính 
đến mức đền bù rủi ro hệ thống 38
Đa dạng hóa danh mục 
đầu tư (DMĐT)
không thể giảm thiểu rủi ro hệ thống
giảm thiểu rủi ro phi hệ thống
DMĐT chỉ chịu tác động 
của rủi ro hệ thống
(rủi ro phi hệ thống bằng 0)
Đa dạng 
hóa tốt
Tỷ suất sinh lời từ DMĐT
là TSSL thị trường (Rm) 
hay lãi suất thị trường
(1)
(2)
38
Độ lệch chuẩn của 
danh mục đầu tư
Rủi ro hệ thống
Rủi ro phi hệ thống
Số lượng các
loại cổ phiếu
39
Mối quan hệ giữa độ lệch chuẩn của DMĐT với 
số lượng chứng khoán trong DMĐT 
39
40
40
Th.S Bùi Ngọc Mai Phương 11/13/19
11
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
3.4.1. Tỷ suất sinh lời của DMĐT
3.4.2. Rủi ro của DMĐT
41
41
3.4.1. Tỷ suất sinh lời của DMĐT
Rp =
Wi : Trọng số đầu tư vào khoản đầu tư i
Ri : Tỷ suất sinh lời kỳ vọng của khoản đầu tư i
n : Số lượng các khoản đầu tư trong danh mục
42
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
42
Danh mục đầu tư TSSL kỳ vọng
100% CP A 8,5%
100% CP B 16,0%
30% CP A và 70% CP B
40% CP A và 60% CP B
43
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
3.4.1. Tỷ suất sinh lời của DMĐT
Ví dụ 9:
43
3.4.2. Rủi ro của DMĐT
Phụ thuộc
- Rủi ro của từng khoản đầu tư có trong danh mục
- Mối quan hệ rủi ro giữa các khoản đầu tư đó với
nhau.
Rủi ro của danh mục đầu tư được đo lường
bởi phương sai và độ lệch chuẩn của DMĐT.
44
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
44
Th.S Bùi Ngọc Mai Phương 11/13/19
12
3.4.2. Rủi ro của DMĐT
- Độ lệch chuẩn của danh mục (𝛔𝐩) đo lường mức độ phân
tán của các TSSL thực tế so với TSSL kỳ vọng của DMĐT
n: số chứng khoán trong DMĐT
Wi, Wj : Tỷ trọng vốn đầu tư vào chứng khoán i và j
Cov(i,j) : Đồng phương sai của chứng khoán i và j
Cov(i,j) = ρi j x σC x σD
ρij : Hệ số tương quan kỳ vọng giữa TSSL của chứng khoán i và j
45
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
𝛔𝐩 = 𝐕𝐚𝐫𝐩
45
46
CK 1 2 3 ... N
1 W1W1COV(1,1) W1W2COV(1,2) W1W3 COV(1,3) W1WN COV(1,N)
2 W2W1COV(2,1) W2W2COV(2,2) W2W3 COV(2,3) W2WN COV(2,N)
3 W3W1COV(3,1) W3W2COV(3,2) W3W3 COV(3,3) W3WN COV(3,N)
N WNW1COV(N,1) WNW2COV(N,2) WNW3 COV(N,3) WNWN COV(NN)
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
3.4.2. Rủi ro của DMĐT
Ma trận xác định 𝐕𝐚𝐫𝐩 của danh mục gồm n chứng khoán.
46
47
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
3.4.2. Rủi ro của DMĐT
Ma trận xác định 𝐕𝐚𝐫𝐩 của danh mục gồm 2 chứng khoán.
CK A B
A
WA WA Cov(RA,RA) =
WA2 σE2 WA WB Cov(RA,RB) =WA WB ρAB σE σF
B
WB WA Cov(RB,RA) =
WA WB ρAB σE σF WB WB Cov(RB,RB) =WB2 σF2
47
3.4.2. Rủi ro của DMĐT
- Độ lệch chuẩn của danh mục đầu tư 2 tài sản
𝛔(𝐀,𝐁) = 𝐕𝐚𝐫(𝐀,𝐁)
WA+ WB = 1
Cov(A,B) = ρAB × σE × σF
Cov(RA,RB) = ? và ρAB = ?
48
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
48
Th.S Bùi Ngọc Mai Phương 11/13/19
13
3.4.2. Rủi ro của DMĐT
- Đồng phương sai (Covariance - Cov)
Phản ánh mối quan hệ rủi ro của các khoản đầu tư
trong danh mục bằng cách đo lường mức độ tác động
qua lại lẫn nhau giữa TSSL của chúng.
Xác định Cov (RA,RB):
+ Từ dữ liệu phân phối xác suất
+ Từ dữ liệu quá khứ
49
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
49
3.4.2. Rủi ro của DMĐT
- Đồng phương sai (Covariance - Cov)
+ Xác định Cov (RA,RB) từ dữ liệu phân phối xác
suất
pi xác suất xảy ra các tình huống i và ∑CIJK pC = 1
n: số tình huống xảy ra
50
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
𝐂𝐨𝐯 𝐑𝐀, 𝐑𝐁 =
50
3.4.2. Rủi ro của DMĐT
- Đồng phương sai (Covariance - Cov)
+ Xác định Cov (RA,RB) từ dữ liệu quá khứ
51
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
𝐂𝐨𝐯 𝐑𝐀, 𝐑𝐁 =
𝐂𝐨𝐯 𝐑𝐀, 𝐑𝐁 =
51
Ví dụ: DMĐT gồm 2 khoản đầu tư vào dự án A và B.
Tính Cov(RA,RB) và nhận xét ?
52
Năm RA RB
1 -12,00% 30,00%
2 8,00% 26,00%
3 16,00% -20,00%
4 22,00% 28,00%
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
52
Th.S Bùi Ngọc Mai Phương 11/13/19
14
3.4.2. Rủi ro của DMĐT
Đồng phương sai Cov(RA,RB)
53
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
Cov (RA,RB) RA & RB 
Lớn hơn 0 Biến động cùng chiều
Nhỏ hơn 0 Biến động ngược chiều àA và B có thể bù đắp rủi 
ro cho nhau trong DMĐT
Bằng 0 Biến động độc lập nhau
53
3.4.2. Rủi ro của DMĐT
- Hệ số tương quan (coefficient of correlation - ρAB)
Thể hiện mối quan hệ cùng hay ngược chiều giữa TSSL của
hai khoản đầu tư.
54
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
𝛒𝐀𝐁 = 𝐂𝐨𝐯(𝐑𝐀, 𝐑𝐁)𝛔𝐀 × 𝛔𝐁
-1 ≤ ρAB ≤ 1
54
55
3.4. Lợi nhuận và rủi ro của danh mục đầu tư𝛒𝐀𝐁 RA & RB ρEF = -1 Biến động ngược chiều hoàn toàn à có thể 
giảm thiểu hoàn toàn rủi ro
-1 < ρEF < 0
(Cov RE, RF < 0) Biến động ngược chiều à có thể giảm rủi roρEF = 0
(Cov RE, RF = 0) Biến động hoàn toàn độc lập với nhau à không có tương quan
0 < ρEF < 1
(Cov RE, RF > 0) Biến động cùng chiều à không thể giảm thiểurủi roρEF = 1 Biến động cùng chiều hoàn toàn à không thể 
giảm thiểu hoàn toàn rủi ro
55
3.4.2. Rủi ro của DMĐT
Độ lệch chuẩn của danh mục đầu tư đặc biệt
Với ρAB = 1 à 𝛔(𝐀,𝐁) =  . .+  . . )
Với ρAB = -1à 𝛔(𝐀,𝐁) =  . .−  . . )
56
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
56
Th.S Bùi Ngọc Mai Phương 11/13/19
15
Ví dụ: DMĐT gồm 2 khoản đầu tư vào dự án A và B.
Tính ρAB và nhận xét ?
57
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
57
Ví dụ: DMĐT gồm 2 khoản đầu tư vào dự án A và
B. Biết WA = 30% và WB = 70%. Tính REF, σ AB?
58
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
58
vĐộ lệch chuẩn bình quân gia quyền của DMĐT!σP = σA x WA + σB x WB
Ý nghĩa: so sánh mức độ rủi ro của DMĐT và rủi ro
của 2 chứng khoán riêng lẻ.
59
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
59
Hệ quả:
ü σP càng thấp hơn !σP và càng nhỏ hơn độ lệch
chuẩn của 1 hoặc cả 2 chứng khoán à kết hợp 2
chứng khoán này càng làm giảm rủi ro của DMĐT.
ü ρEF < 1 ó σP < !σP
ü ρEF càng tiến về -1 ó σP càng nhỏ hơn !σP
60
3.4. Lợi nhuận và rủi ro của danh mục đầu tư
60
Th.S Bùi Ngọc Mai Phương 11/13/19
16
ỨNG DỤNG TIN HỌC
61
Các gía trị của 
một tài sản
Hàm tính Excel
Dữ liệu quá khứ Dữ liệu dự báo xác suất
TSSL kỳ vọng
AVERAGE (number1, 
number2, ...)
SUM (khối giá trị xác suất * khối giá trị 
tính toán)
Phương sai
VAR (number1, 
number2, ...)
SUM {(khối giá trị tính toán – tỷ suất sinh 
lời kỳ vọng)^2 * khối giá trị xác suất}
Độ lệch chuẩn
STDEV (number1, 
number2, ...)
SQRT(var)
SQRT(var)
61