Bài giảng môn Vật lý đại cương 2 - Chương 7: Nguyên tử Hydro

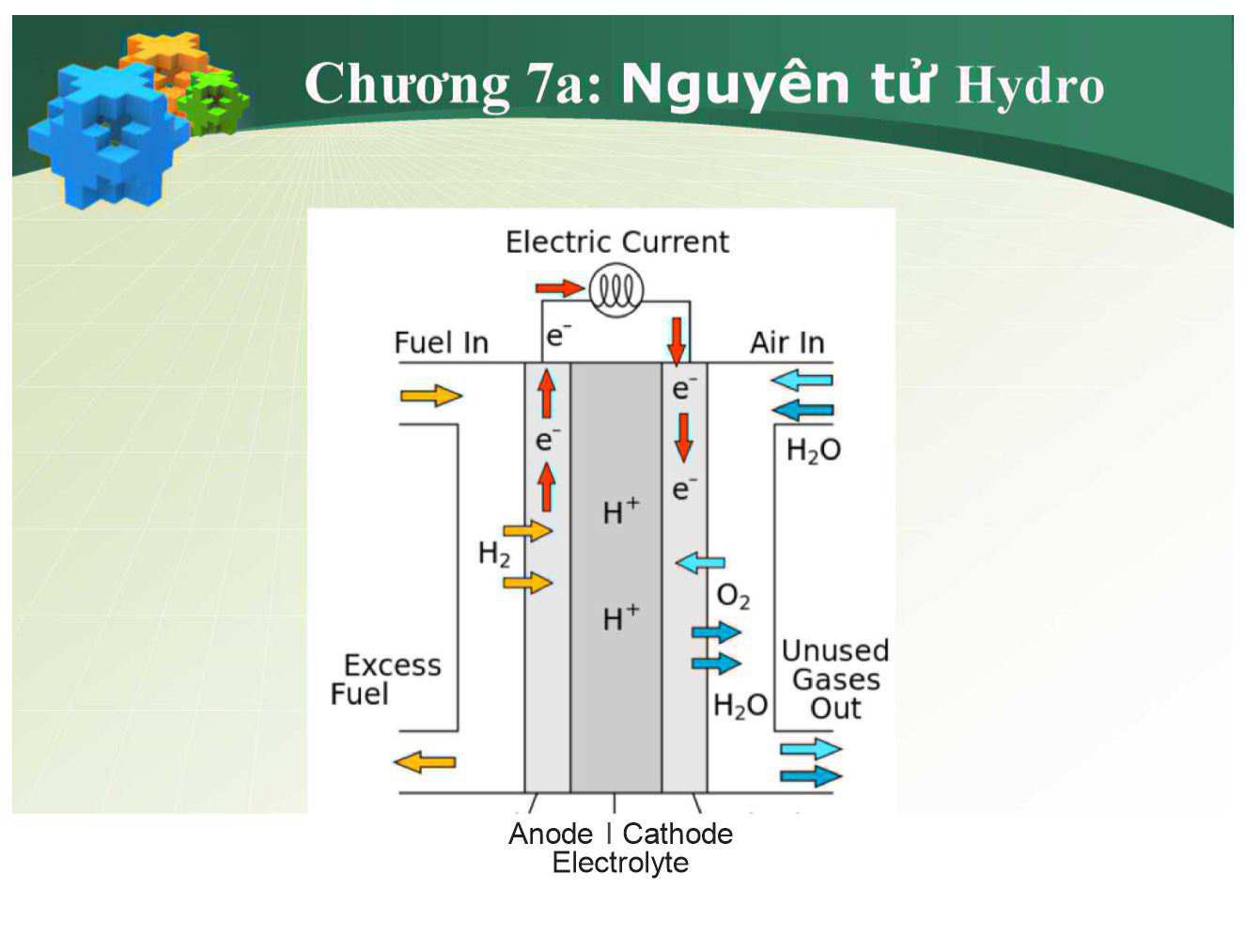
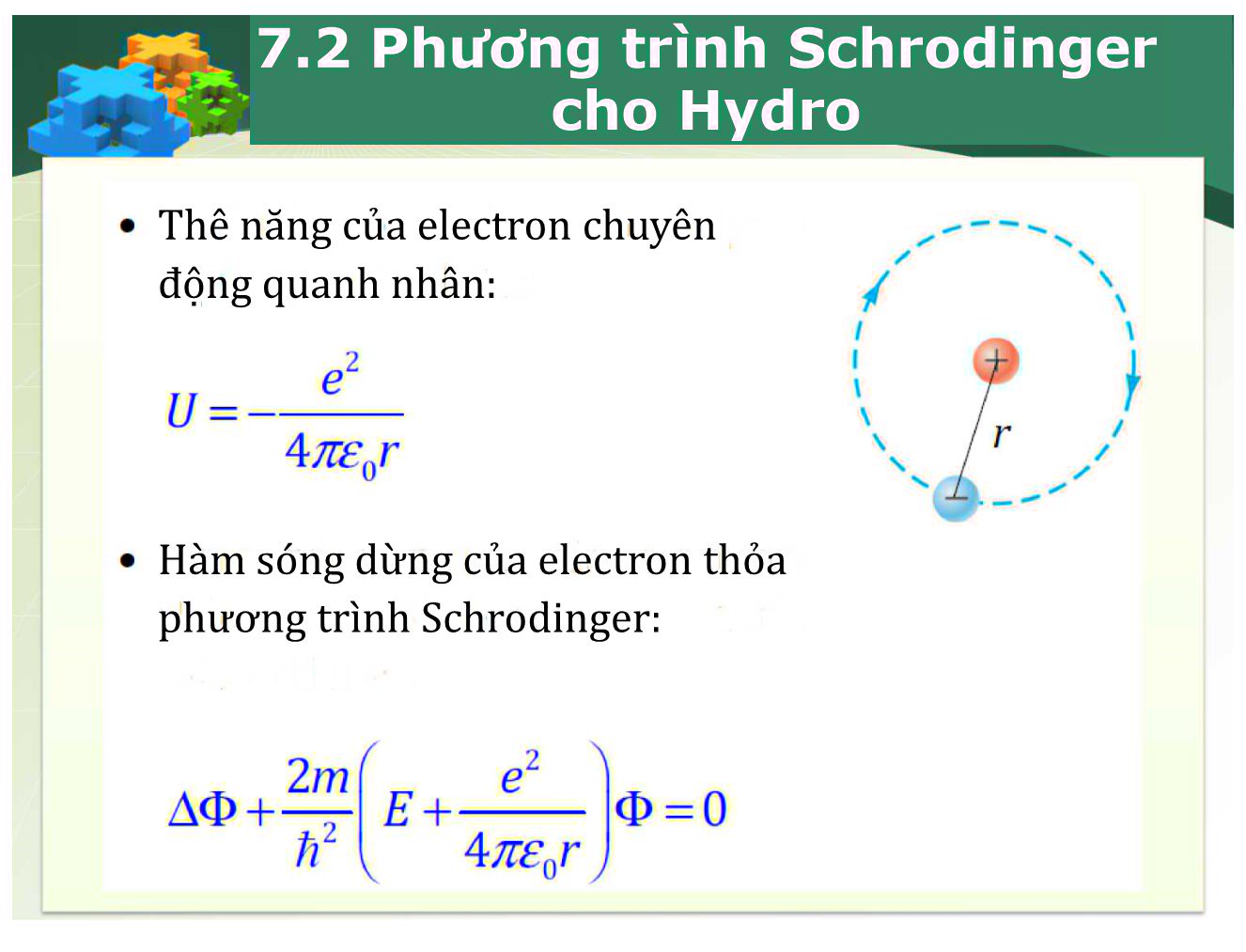
Anode I Cathode
Electrolyte
Chương 7a: Nguyên tử Hydro
7.1 Phổ nguyên tử Hydro
Phương trình Schrodinger cho Hydro
Năng lượng electron
Hàm sóng electron
Mật độ xác suất electron
Hình dạng đám mây electron
Spin electron
7.2 Phương trình Schrodinger cho Hydro
Thê năng của electron chuyên động quanh nhân:
Hàm sóng dừng của electron thỏa phương trình Schrodinger:
7.2 Phương trình Schrodinger cho Hydro
7.2 Phương trình Schrodinger cho Hydro
X	/
Hàm sóng trong tọa độ cầu có dạng:
• Mỗi hàm sóng hay trạng thái được xác định bởi một bộ ba số lượng tử (n, /, rrí).
n = 1,2,3...
/ = 0,l,2,...,n-l m = 0,±l,±2,...,±/
ỉ: số lượng tử quỹ đạo ÌTT. SỐ lượng tử từ
47TcoT
Sử dụng phương pháp phân ly biến số.
-0(rTỡ, sp) = ỉỉ(r) -Y(0,ự>)
2me
1 9
y(ớ,<p)sinớỡổ [ dỡ _
1	ỡ2y(ớ,^)
y (ớ, Ể£>) sin2 ớ dip2
Phương trình có nghiệm đơn tộ, giới nội và liên tục khí À xác định.
(r)\ 2me
r ) h2r2
y(ớ, </?) sin ớ dỡ
1 ỡ2Y(ff, _ Y (ớ, ự?) sin2 ớ
Nghiệm của phương trình vi phân có dạng.
9?) =	v)
6=1 khi m < 0
(cosớ)
Sõ lượng tử chính :
Sõ lượng tử orbital:
Sõ lượng từ từ :
■ Hằng số
Trong đó
Đa thức Legendre
sin
> Một số dạng hàm:
Trong đó <70 là bán kính Bohr
ao =
> Năng lượng của electron:
ĨI2 2(4tt£o)2/ĩ2 n2 2meŨQ
y0,0 = (2-/^)
-T— cosớ
4tt
BÍnỡe-^
8tf
4tt£o^2
mee2
Khi electron chuyển từ mức năng lượng cao về một mức thấp hơn, nguyên tử phát một photon có năng lượng:
he
me
n2 n
và bước sóng:
me
2	„2
*. 7.1 Pho nguyên tử Hydro (1)
Xác suất tìm thấy e- trong một thể tích dV:
Mât đô xác suất
Xác suất tìm thấy e“ trong một vỏ cầu có bề dày đr.
Mật độ xác suất theo khoảng cách
Xác suất tìm thấy e" trong một góc khối cKì-.
Mật độ xác suất theo góc khối
hc
n Quỹđạo Bán kính qđ	rn = n2r0 r0= 5,3.10 11m Ban kinh Borh
5	O	r5 = 52r0
Ỵ chàm
v Pfundt
4	N	r4 = 42r0
3 lam
LV Brackett
3	M	r = 3\
a đỏ	'
rvvPaschen
2	L	r = 22r0
rwv Balmer
1	K	r, = 12r0	,
rv Lyman
6	P	r = 62r0	ô tím
= Ef - Ei
Vd. 5,6,10,11,13, 15, 17, 19, 24, 28, 32,33, 35, 39.
Sơ đồ
bị kích thích đến mức NL cao hơn E1->2->3,....
Electron có thể:
giải phóng NL để trở về mức thấp hơn E...->3,->2->1
NL được xđ bởi (n,l,m,j) => Qui luật chuyể’n mức NL:
Chỉ xét đến n (số lượng tử chính): Am * 0
Chỉ xét đến cả n và l (số lượng tử quỹ đạo): An * 0	Al = ±1
Nếu đặt 2. vào từ trường ngoài (ko tính spin) thì phải có thêm qui tắt chọn lựa cho m (số lượng tử từ): Am = 0,±1
Nếu ở 2. có tính thêm spin (ko có từ trường ngoài) thì phải có thêm qui tắt chọn lựa cho j (số lượng tử toàn phần). Aj = 0,±1
= -
13,6-ỊrCeKJ
n
L
Lz = hm
năng lượng
• momen động lượng
ơ môi trạng thái xác định bởi một bộ ba số lượng tử (n, I, ĩri), electron có:
• momen động đối với một trục z
Vòng tròn bán kính L
Ở trạng thái có / = 2 momen động là:
Hình chiếu momen động , trên trục z:
■
Lz = mỉĩ
• L chỉ có thể có một số hướng xác định - sự lượng tử hóa không gian.
Vd. 40,42,44,50
Trong không gian vectơ L nằm trên một mặt nón và quay quanh trục z.
7.4 Hàm sóng electron (5)
Nguyên tử kim loại kiềm
>
có 2 electron.
có 2(2+1) = 6 electron
có 2 electron.
có 2(2+1) = 6 electron có 2(4+1) = 10 electron
Môi lớp K, L, M, ... được chia thành các lớp con s, p, D...
Mỗi lớp con có 2(2£ + 1) electron.
n = 1 : có một lớp con s, số electron tối đa là 2 tương ứng với £ — 0 n = 2 : có hai lớp con s và p.
Lớp con s tương ứng vối £ — 0
Lớp con p tương ứng với £ = 1
n = 3 : có 3 lớp con s, p và D.
Lớp con s tương ứng với £ = 0
Lớp con p tương ứng với £ — 1
Lớp con D tương ứng với £ — 2
n = 4 : có 4 lớp con s, p, D và F.
Lớp con s tương ứng vổi £ = 0
Lớp con p tương ứng với £ — 1
Lớp con D tương ứng với £ — 2
có 2 electron.
có 2(2+1) = 6 electron có 2(4+1) = 10 electron có 2(6+1) = 14 electron
Lớp con F tương ứng với £ = 3
n=4; l=3; F
Rh
n=4; l=2; D
n=4; l=1; P
n=4; l=0; S
ị ị ị ị
n=3; l=2; D
S P D F
n=3; l=0; S
n=2; l=1; P
n=2; l=0; S
n=1; l=0; S
1
m
Vd.72
l=1
P
l=1
P
l = 0, 1, 2, 3,... n-1
Al = ±1
En,l
Phụ I: 2P --- nD
0	1	2
Chính: 2S — nP
ẸỊỊỊỊỊ
Itltltltlt
Cơ bản: 3D — nF
m= -2
n = 1, 2, 3, 4, ...
KB0 muuut 'ỉ,
Phụ II: 2P --- nS
X ỉ Ạ f
l=1
P
/=2 D
iĩlĩKKHH F
m= -3	-2	-1	0	1	2	3
7.4 Hàm sóng electron (5)
Nguyên tử kim loại kiềm
I Moment động lượng (moment orbital).
Electron chuyển động không có quỹ đạo
Vector moment động lượng của electron L không có hướng xác định.
Giá trị của moment động lượng của electron lại là một đại lượng xác định và nó nhận các giá trị gián đoạn:
L =	+ l)/l; £ = 0,1,2,-,n-l
Hình chiếu theo phương z của vector moment động lượng của electron cũng bị lượng tử hoá
Lz = m/z; m — 0, ±1, ±2, ■ • • , ±£
I Moment từ.
Electron chuyển động quanh hạt nhân sẽ tạo thành dòng điện, dòng điện này có moment từ:
H = — -	L
2me
Nguyên tử kim loại kiềm
Hình chiếu theo phương z của moment từ:
Mz = -7ẽ~lz = ~m7Ẽ~ = “Wb
2me	2me
Maneton Bohr: Mb = 9	= 10 23A.m2
Hình chiếu moment từ của electron chuyển động quan hạt nhân lên một phương bất kỳ luôn bằng sô' nguyên lần của một đại lượng không đối maneton Bo hr, nghĩa Ị à nó bị Ịượng tử hoá.
Hiệu ứng Zeeman
Khi nguyên tử phát sáng đặt trong từ trường, vạch quang phổ bị tách tành nhiều vạch nằm sát nhau.
Sự tách vạch phổ tuân theo quy tắc lọc lựa :
Am = 0, ±1
Mỗi một vạch phổ bị tách thành 3 vạch, vạch ở giữa trùng với vạch cũ (vạch khi không có từ trường).
u; V = V ± ——D
h
>
n=4; l=3; F
n=4; l=2; D
m=2
m=1
g BB
m=0
m
n=3; l=2; D
n=3; l=0; S
n=2; l=1; P
m
n=2; l=0; S
n=1; l=0; S
l=0
1
m
Vd.43
1=2
Dj
l=1
P
l=1
P
Phụ I: 2P --- nD
Chính: 2S — nP
Cơ bản: 3D — nF
KB0 mntmt
m= -2	-1	0	1	2
m=1 m=0
E - E Am f ' = -^—1 + —— h	h
M l=1 _ J P
1=2 D
l=3 F m= -3	-2	-1	0	1	2	3
l m = 0, ± 1, ± 2,	± l.	ịảt -	AE = m^.B
Am = 0; ± 1
10-22 A m
E' = E + m^B B
7.4 Hàm sóng electron (5)
n=4; l=0; S
Phụ II: 2P --- nS
X ỉ Ạ f
Nguyên tử kim loại kiềm
Khái niệm Spin:
Trên thực tế, các vạch phổ không phải là các vạch đơn mà nó được hợp thành bởi nhiều vạch nhỏ. Các vạch phố này gọi là vạch phổ kép.
Ví dụ: vạch phổ màu vàng của Na gồm 2 vạch có bước sóng 5890 Ả° và 5896 Ẩ°'.
Thực nghiệm chứng tỏ rằng: moment từ lớn gấp 2 lần so với lý thuyết:
me 2me
Moment từ liên quan đến sự chuyển động quay của các hạt mang điện:
Chỉ sử dụng sự chuyển động của electron quanh hạt nhân không thể giải thích được hiện tượng này.
Người ta giả thiết rằng, electron có thêm phần chuyển động tự quay quanh một trục riêng của nó.
Thành phần đóng góp vào moment từ sẽ có thêm thành phần moment spin, moment spin đóng vai trò như moment động lượng riêng.
>
Nguyên tử kim loại kiềm
Hình chiếu của moment spin:
s = —
ms\ số lượng tử hình chiếu spin.
Spin là một khái niệm thuần túy lượng tử, không có khái niệm spin trong cơ học cổ điển. Giá trị của moment spin:
5: số lượng tử spin.
Hình chiếu của moment từ riêng của spin trên trục z:
me
Giá trị này hoàn toàn phù hợp với thực nghiệm
tá
Vector moment từ:
Nguyên tử kim loại kiềm
Trạng thái và năng lượng của electron trong nguyên tử: Moment toàn phần của electron:
Giá trị của moment toàn phần
Số lượng tử moment toàn phần
j =
Trạng thái của electron trong nguyên tử được xác định bởi 4 số lượng tử:
n, -Ể, m, ms
Các tương tác:
Tương tác giữa moment từ quỹ đạo và moment từ riêng
Tương tác giữa các moment từ riêng của các electron trong nguyên tử.
Khỉ tính đến spin, có thêm phần năng lượng bổ sung phụ thuộc vào hướng của spin.
Năng lượng toàn phần của electron trong nguyên tử phụ thuộc vào 3 số lượng tử n, £, j
Môi mức năng lượng trước đây bị tách thành hai mức tương ứng với
Cấu trúc năng lượng này gọi là cấu trúc tế vi, khoảng cách giữa hai mức năng lượng này không lớn lắm.
Ký hiệu các mức năng lượng của electron: n 2Xj
Số lượng tử chính: n = 1,2,3, • • •
Chỉ số 2 thể hiện cấu tạo bội kép của mức năng lượng.
Các trạng thái x= s, P,D, ... tương ứng với Ể — 0,1, 2, • • •
Số lượng tử moment toàn phần
Ký hiệu cho trạng thái của electron hóa trị: TiXj
Nguyên tử kim loại kiềm
> Bảng các trạng thái và các mức năng lượng của electron hóa trị trong nguyên tử H và kim loại kiềm.
■
n
£
y
Trạng thái của electron hóa trị
Mức năng lượng (với hệ số -Tí)
1
0
-
tl/2
ls±l/2
1 2Sl/2
2
0
1
±1/2
1/2
3/2
2s±l/2
2pi/2
2í*3/2
2 25±i/2
2 2A/2
2 2 ^3/2
3
0
1
2
±1/2 í 1/2
1 3/2
í 3/2
1 5/2
2s±1/2
3pi/2
3p3/2
3^3/2
3^5/2
2S±i/2
2A/2
3 2^3/2
3 2 ^3/2
3 2j^5/2
Nguyên tử kim loại kiềm
>
Aj = -ỉ, ta có:
>
Aj = 0, ta có:
Aj = 1, ta có:
Cấu tạo bội của vạch phổ:
Tương tự đối với số quy tắc chọn lọc đối với số lượng tử quỹ đạo, khi electron chuyển mức cũng phải tuân theo quy tắc chọn lọc đối với số lượng tử7.
Ví dụ: Xét chuyển mức của dãy chính (A£ = — 1): V — 2S — 3P AJ = Qf ta có	3
n=4; l=3; F
n=4; l=2; D
Aj = 0; ± 1
n=3; l=2; D
n=3; l=0; S
n=2; l=1; P
n=2; l=0; S
n=1; l=0; S
1
m
Vd: 51,52, 54, 70, 62,63, 69
1=2
Dj
l=1
P
l=1
P
ct.t.tlỉlỉ itintitint
3D.,.
3/2
2 -1 1/2
2P,,„
3/2
Phụ I: 2P --- nD
3D5/2
Chính: 2S — nP
Cơ bản: 3D — nF
KB0 mntmt
5 = 1/2
l ±1
2
m= -2	-1	0	1	2
L = mh
M l=1 _ J P
1=2 D
l=3 F m= -3	-2	-1	0	1	2	3
ms = ±1/2
7.4 Hàm sóng electron (5)
n=4; l=0; S
f	5 1
Phụ II: 2P --- nS
X ỉ Ạ f
Nguyên tử kim loại kiềm
Nguyên lý loại trừ Pauli:
ở mỗi trạng thái lượng tử xác định bởi 4 số lượng tử n, ể, m, ms chỉ có thể có tối đa một electron.
Từ công thức tính số các trạng thái lượng tử của electron ứng với mỗi giá trị n
n— 1
J2(2£+ 1) = n2
£=0
Nếu tính đến số lượng tử spin, mỗi một giá trị ỉ, có hai giá trị ms — ±1/2 tức là có 2n2 trạng thái lượng tử. Tức là với mỗi giá trị n có tối đa 2w2 electron.
Các lớp electron quanh hạt nhân:
/7=1 tương ứng với lớp K, có tối đa 2 electron.
n = 2 tương ứng với lớp L, có tối đa 8 electron.
n = 3 tương ứng với lớp M, có tối đa 18 electron.
n = 4 tương ứng với lớp N, có tối đa 32 electron.
>
Nguyên tử kim loại kiềm