Bài giảng môn Vật lý đại cương 2 - Chương 3, Phần b: Nhiễu xạ
Hiện tượng nhiễu xạ
• Nhiễu xạ là hiện tượng sóng đi vòng qua vật cản;
• Sau đó các phân khác nhau của sóng giao thoa ờ phía sau vật cản, tạo nên những vùng sóng có biên độ cực đại và cực tiểu xen kẽ nhau.
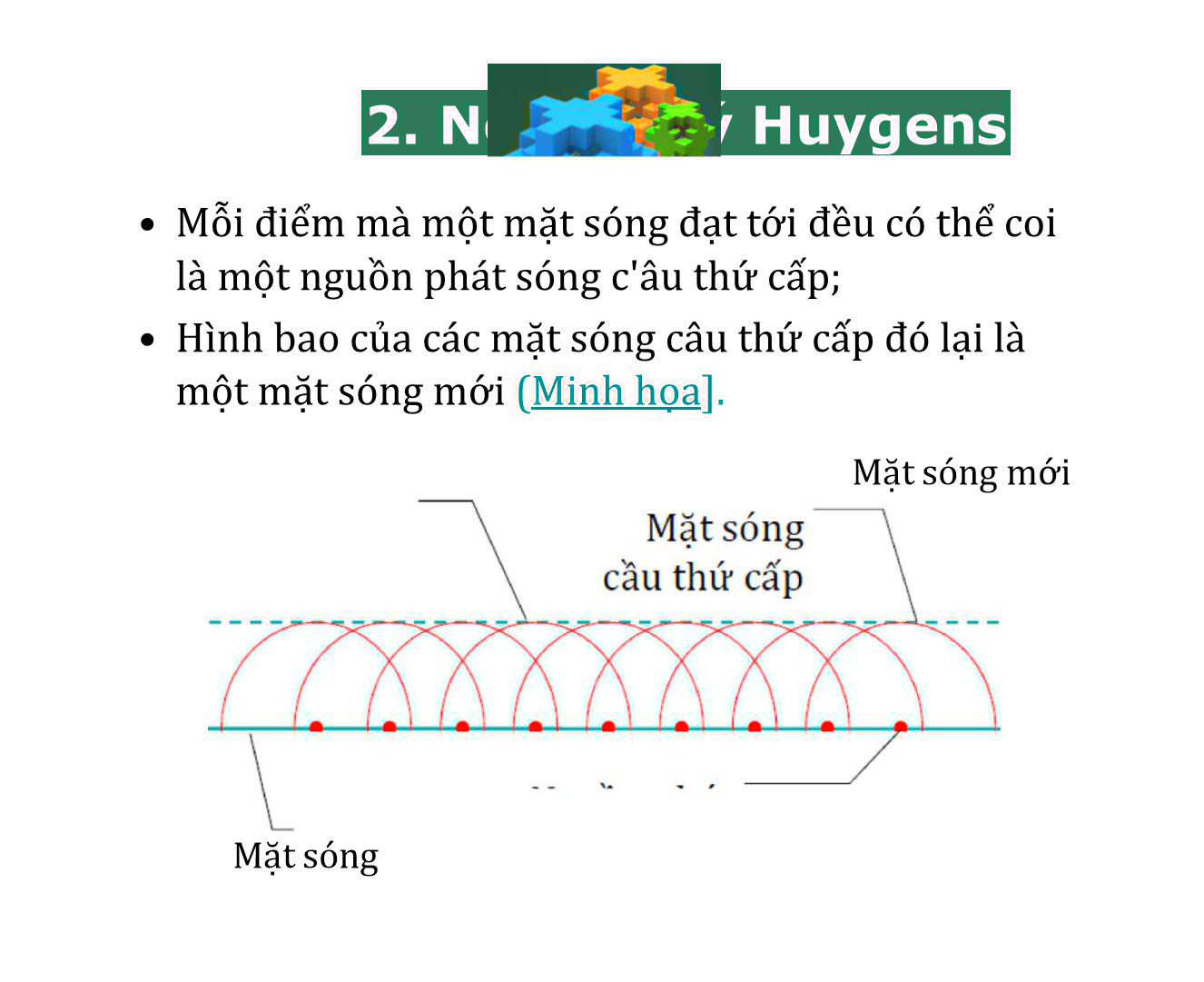
• Mỗi điểm mà một mặt sóng đạt tới đều có thể coi là một nguồn phát sóng c'âu thứ cấp;
• Hình bao của các mặt sóng câu thứ cấp đó lại là một mặt sóng mới (Minh họa].
3a. Hiện tượng
3b. Phương pháp đới cầu Fresnel
3a. Tính chất đới cầu Fresnel 3a. Sóng thứ cấp phát từ đới cầu Fresnel
3a. Biên độ tổng hợp khi không có màn chắn
Trang 1

Trang 2

Trang 3

Trang 4
Trang 5
Trang 6
Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng môn Vật lý đại cương 2 - Chương 3, Phần b: Nhiễu xạ", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng môn Vật lý đại cương 2 - Chương 3, Phần b: Nhiễu xạ
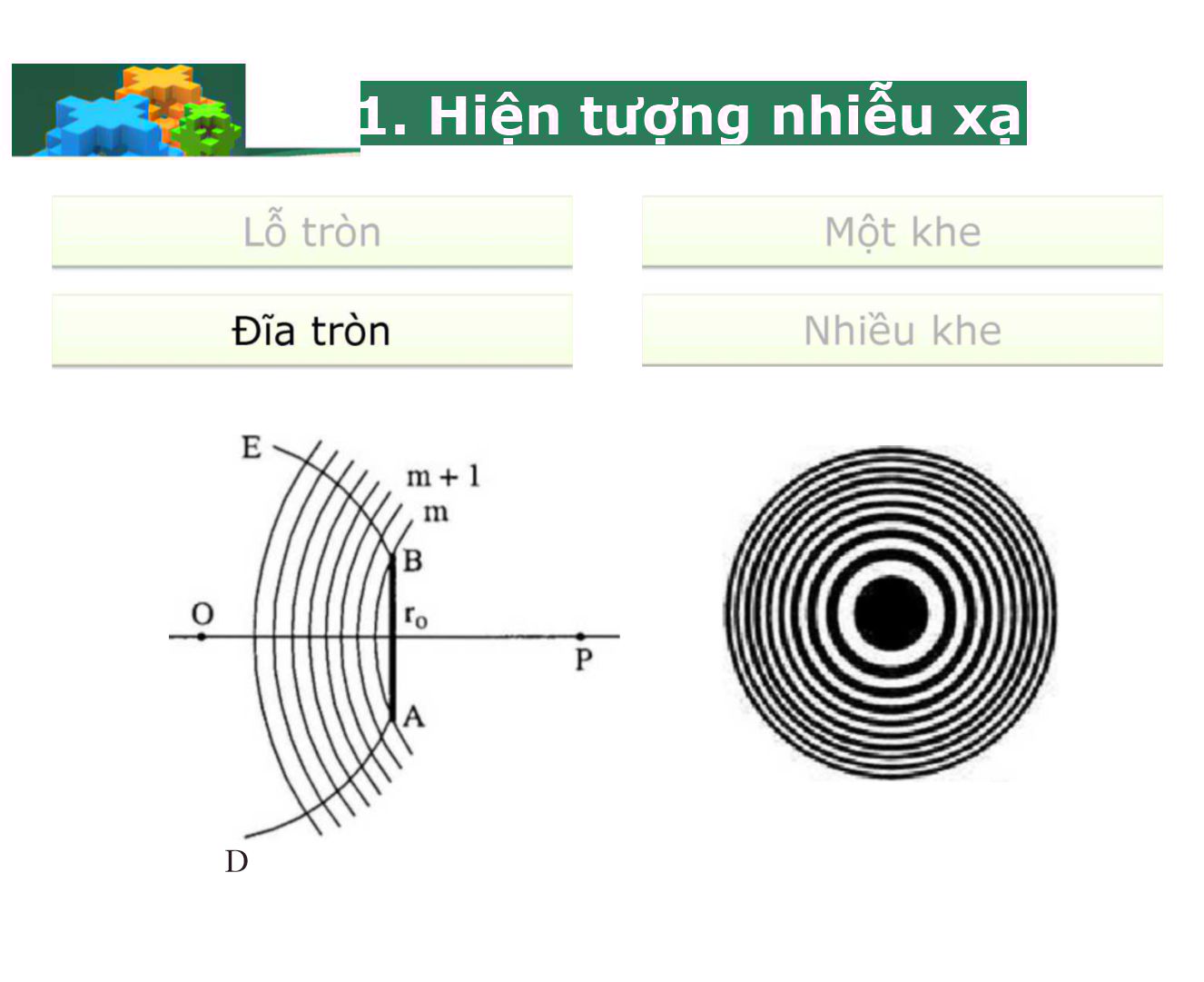
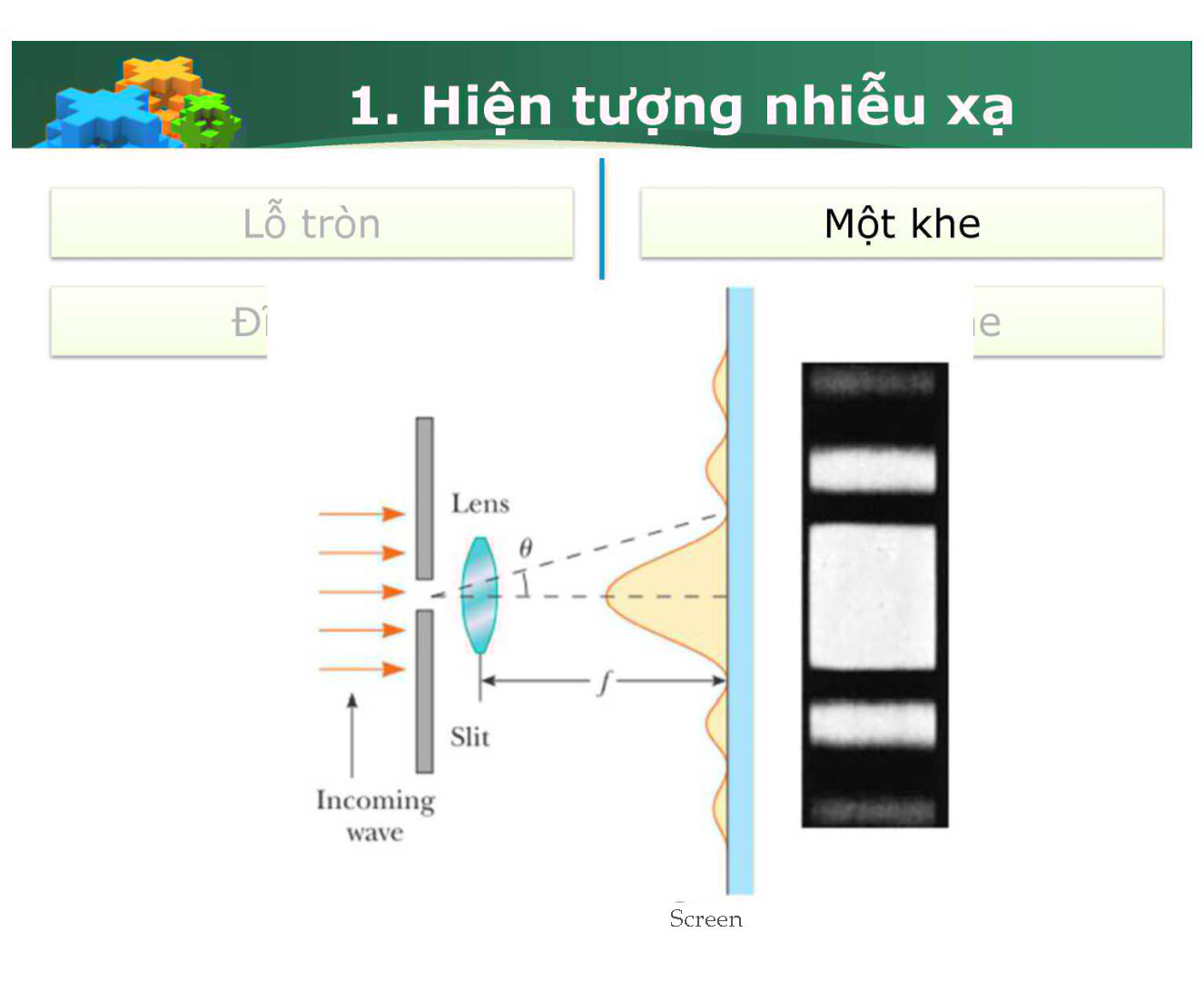
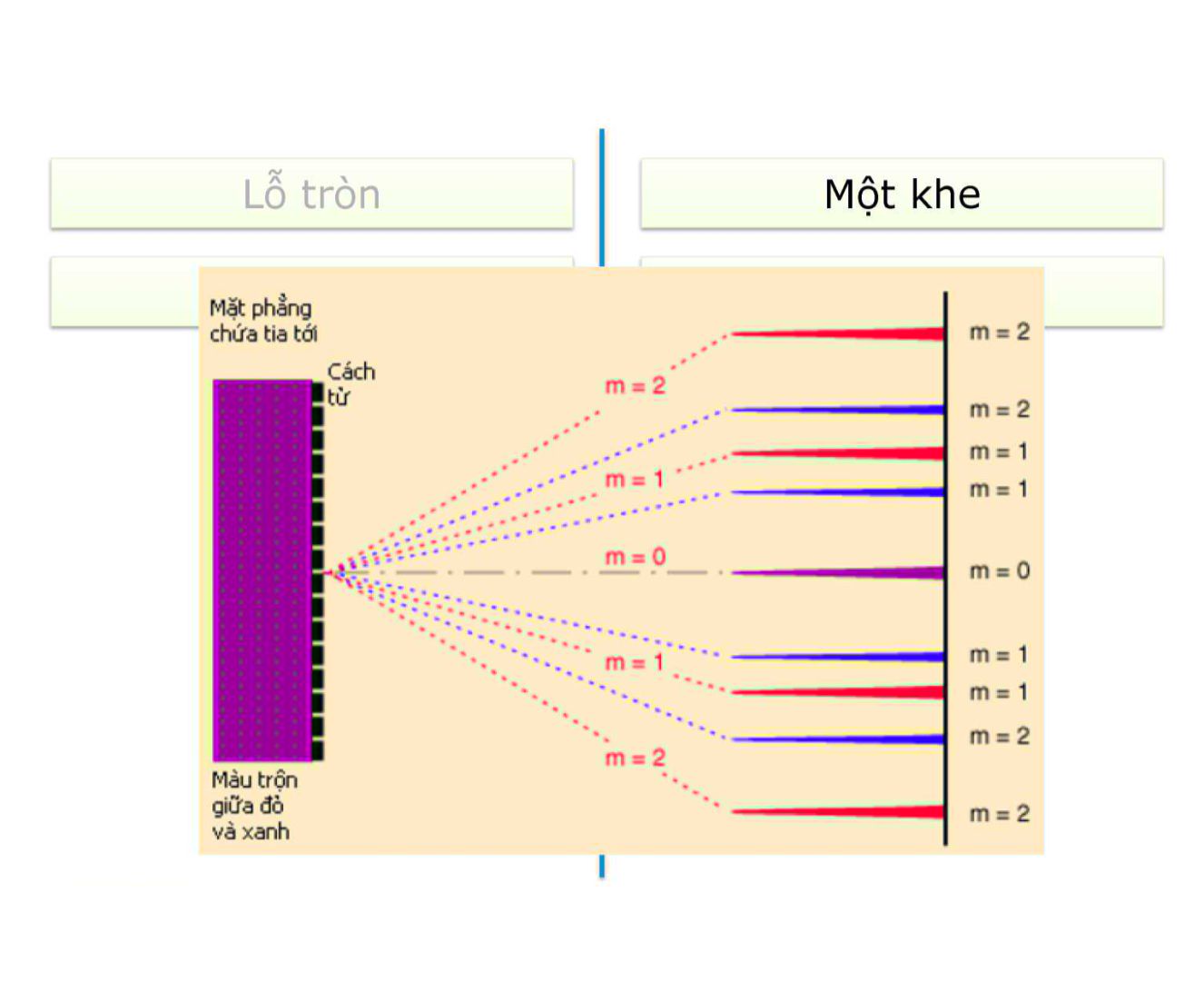
Nhiêu xa Chương 3b: Nhiếu xạ Jguyen lý Huygens Nhiêu xạ trên lỗ tròn Hiện tượng Nhiêu xạ trên nhiều khe hẹp Nhiêu xạ trên khe hẹp Nhiễu xạ tia X la. Hiện tượng nhiễu xạ • Nhiễu xạ là hiện tượng sóng đi vòng qua vật cản; • Sau đó các phân khác nhau của sóng giao thoa ờ phía sau vật cản, tạo nên những vùng sóng có biên độ cực đại và cực tiểu xen kẽ nhau. ■ ■ ■ ■ 1. Hiện tượng nhiễu xạ Môt khe Lô tròn 1. Hiện tượng nhiêu xạ D Screen 1. Hiện tượng nhiễu xạ Mỗi điểm mà một mặt sóng đạt tới đều có thể coi là một nguồn phát sóng c'âu thứ cấp; Hình bao của các mặt sóng câu thứ cấp đó lại là một mặt sóng mới (Minh họa]. Mặt sóng mới Mặt sóng Nguồn phát sóng cầu thứ cấp 3a. Hiện tượng 3b. Phương pháp đới cầu Fresnel 3a. Tính chất đới cầu Fresnel 3a. Sóng thứ cấp phát từ đới cầu Fresnel 3a. Biên độ tổng hợp khi không có màn chắn 3b. Phương pháp đới cầu Fresnel Mặt sóng cãu s Đới Fresnel bậc 4 b + 4(Ấ/2) ỉ)+ 2(1/2) b + Ả/2_..-. b + 3(Ằ/2) B 0B = b Đới Fresnel bâc 1 3c. Tính chất của các đới Fresnel • Nếu bậc của các đới không quá lớn thì tất cả đêu có diện tích bằng nhau: À „ TĩabẰ AS —— a + b Với ữ = SO, b = OB. Bán kính biên ngoài của đới bậc m là: 3c. Tính chất của các đới Fresnel [tt] Bán kính r b + 4(Ẳ/2) b + 2(Ẳ/2) b + 3(Ẳ/2) SO - a OB = b Diên tích AS 3d. Sóng thứ cấp phát từ các đới Fresnel Tại điểm quan sát B sóng thứ cấp phát từ các đới Fresnel có tính chất sau: Hai sóng phát ra từ hai đới liên tiếp thì ngược pha nhau, vì quang trình của chúng khác nhau một nửa bước sóng. Biên độ sóng gần bằng nhau, vì các đới có diện tích bằng nhau, và khoảng cách truyền thì chỉ thay đổi rất ít. 3e. Biên độ tổng hợp khi không có màn chắn • Tất cả các đới Fresnel trên mặt sóng đều gửi sóng đến B, biên độ tổng hợp tại B là: A — A1 A2 + A3 A4 +... 'lĩỉ 777—1 m+1 Khi không có màn chắn, biên độ tổng hợp bằng một nửa biên độ của đới thứ nhất. 3e. Biên độ tổng hợp khi lỗ nhỏ 3e. Biên độ tổng hợp khi lỗ nhỏ (tt) • Giả sử lỗ tròn nhỏ chỉ cho đi qua 3 đới Fresnel đâu tiên: • Nêu lỗ tròn chỉ cho đi qua 4 đới đâu tiên: A+Al m = l,3,5... Sô lẻ đới đi qua: J 2 2 cực đại |Ạ . Sô chẵn đới đi ' - /77 = 2,4,6... 2 2 qua: cực tiểu Chiêu một chùm sáng song song, bước sóng 6.10A(-6)m vuông góc r 9 r"v' . với màn chăn có lô tròn bán kính 0,6mm. Điêm M trên trục lô cách lô một khoảng bao nhiêu thì M sẽ sáng nhất? mabà Do chùm ánh sáng song song nên a rất lớn: mabà I—— ——— = V mbà Điêm M sáng nhất khi cho sô lẽ đới câu qua => m=1. 3. Nhiễu xạ qua đĩa tròn 4a. Hiện tượng 4b. Các nguồn thứ cấp 4c. Vị trí các vân 4d. Phân bô cường độ sáng • Màn cách xa Incoming I wave \ 4a. Nhiễu xạ trên khe hẹp: hiện tượng • Sóng tới phẳng đơn sắc. khe: các tia cùng góc lệch giao thoa nhau. 4b. Các nguôn thứ cấp Chia mặt sóng trên khe thành nhiêu dải hẹp giống nhau song song với khe; Hiệu quang lộ của hai sóng liên tiếp bằng một nửa bước sóng. 4. Nhiêu xạ trên khe hẹp 4b. Các nguồn thứ cấp (hết) Tại một vị trí trên màn quan sát, các sóng thứ câp có tính chất: Có cùng biên độ, vì các nguồn thứ cấp giống nhau. Khi góc lệch ớ = 0 tất cả các sóng thứ cấp đêu cùng pha. Khi góc lệch ỡ / 0 hai sóng thứ cấp liên tiếp ngược pha nhau, vì hiệu quang trình giữa chúng bằng Ằ/2. 4c. Vị trí các vân ■ A/2 bsinO = 4(Ẳ/2) Nguồn thứ cấp Thấu kính hôi tu Màn quan sát ở tiêu diên 4c. Vị trí các vân (tt) Biên độ tổng hợp ở tâm 0 (ớ = 0) luôn luôn cực đại, tạo nên vân sáng trung tâm. Ở các vị trí khác (ớ + 0) thì biên độ là: Cực tiểu nếu số nguồn thứ cấp là chẵn. Cực đại nếu số nguồn thứ cấp là lẻ. Số nguồn thứ cấp được xác định từ: hsinớ = N-- 2 .. 2ốsinỂ? N = ——— 4c. Vị trí các vân (hết) • Để có cực tiểu thì N phải là một số chẵn, N = 2m, hay: m = ±l,±2... Để có cực đại thì N phải là một số lẻ, N = 2m + Trong công thức trên ta không chọn m = 0 và ỉĩỉ = -1 vì sinỡ = ± A/2Ố nằm trong vân sáng trung tâm. 4d. Phân bố cường độ sáng Màn quan sát Ví dụ 92 2b Trên hình nhiễu xạ qua một khe hẹp vị trí trên màn quan sát ứng với sin 0 = cho vân nào? Bậc nào? sin0 = m + -- — 2 ) b So với điều kiện đề cho ta có => Vân sáng bậc 4 5a. Nhiễu xạ trên nhiều khe hẹp 5b. Vị trí cực đại, cực tiểu 5c. Phân bố cường độ sáng 5d. Ứng dụng của cách tử 5a. Nhiễu xạ trên nhiều khe ■ Xét hệ có N khe song song, bề rộng b, khoảng cách giữa hai khe liên tiếp là đ. Nhiễu xạ trên nhiều khe là sự kết hợp của nhiễu xạ trên từng khe và giao thoa giữa các khe. Khi N rất lớn hệ được gọi là cách tử, còn d là chu kỳ của cách tử. 5b. Vị trí cực đạt cực tiểu I I ■ * ■ Cực đại trung tâm ứng với góc lệch ỡ = 0. Các cực tiểu chính (do nhiễu xạ trên một khe]: m1 =±1,±2.„ bsinớ = m1A Các cực đại chính (do giao thoa giữa các khe) : m2 = ±1,±2... dsinớ =/7?2ấ Giữa hai cực đại chính liên tiếp còn có (TV - 1) cực tiểu phụ và Ị7V - 2) cực đại phụ. 5c. Phân bố cường độ sáng K<A. ! 1 _ Relative Môt khe intensity ■ \ 1 1 % 20 15 10 5 0 5 10 15 20 Cường độ do nhiễu xạ trên ■ một khe Là hình bao của cường độ nhiễu xạ qua nhiêu khe. Số khe trong cách tử Giữa hai cực tiểu chính có các cực đại chính, cực đại phụ, cực tiểu phụ. Nếu cực tiểu chính trùng với cực đại chính thì sẽ không quan sát được cực đại chính. Giữa hai cực đại chính có các cực đại phụ. Giữa hai cực đại phụ là cực tiểu phụ. Nếu hệ có N khe thì giữa hai cực đại chính kế tiếp có: N-1 cực tiểu phụ N-2 cực đại phụ. 5cL. ứng dụng của cách tử Vì các cực đại rất rõ nét và sáng nên cách tử nhiễu xạ được dùng để: Phân tích ánh sáng thành ánh sáng đơn sắc. Phân tích phổ ánh sáng phát từ vật chất. Đo bước sóng ánh sáng. 5. Nhiêu xạ trên nhiều khe hẹp Ví dụ Một cách tử nhiễu xạ có 3 khe hẹp, chu kỳ bề rộng mỗi khe 1,2/m. Ánh sáng đơn sắc bước sóng 0,6ụm hiếu thẳng góc với mặt cách tử. Số cực đại chính tối đa cho bởi cách tử có thể quan sát được là? mẢ . Cực đại nhiễu xạ sin^ = —— <1 d Ả Cực tiểu chính sin ớ = k— < 1 b _ d m < — - Ả k <-- = Ả ~ = 10 0,6 12 = 2 0,6 m = 9 -> CĐ-9.2+1-19 Cực tiểu chính trùng với cực đại chính ... Ả 1. Ả m— = k — m = 5k Nếu k=1 thì m=5 thỏa điều kiện m<10. Từ k=2 trở đi loại. Như vậy có 02 vị trí trùng đó là k=1 và k=-1. Tổng cực đại quan sát được 19-2=17 6a. Nhiễu xạ tia X 6b. Định luật Bragg Ji 6a. Nhiễu xạ tia X ■ Tia X có bước sóng cỡ Angstrom (1 A = 10 "10 m) nên có thể nhiễu xạ trên các khe ở giữa các nguyên tử, phân tử câu tạo nên vật chất. Dùng ảnh nhiễu xạ tia X trên vật chất, các nhà khoa học có thể xác định được cấu trúc của vật chất. Ảnh nhiễu xạ tia X của DNA gợi ý cho Crick và Watson (1953) về cấu trúc chuỗi xoắn kép. Từ đó một ngành mới ra đời - Sinh học phân tử. m = 0,±l,±2... Tia tới Tia nhiễu xa Mặt phẳng nguyên tử 6b. Định luật Bragg • Các cực đại nhiễu xạ tia X trên tinh thể được xác định bởi định luật Bragg: 2c/sinớ = mẢ
File đính kèm:
 bai_giang_mon_vat_ly_dai_cuong_2_chuong_3_phan_b_nhieu_xa.docx
bai_giang_mon_vat_ly_dai_cuong_2_chuong_3_phan_b_nhieu_xa.docx bai-giang-vat-ly-dai-cuong-2-chuong-3b-nhieu-xa_SID12_PID1455750.pdf
bai-giang-vat-ly-dai-cuong-2-chuong-3b-nhieu-xa_SID12_PID1455750.pdf

