Bài giảng môn Vật lý đại cương 2 - Chương 1: Trường điện từ

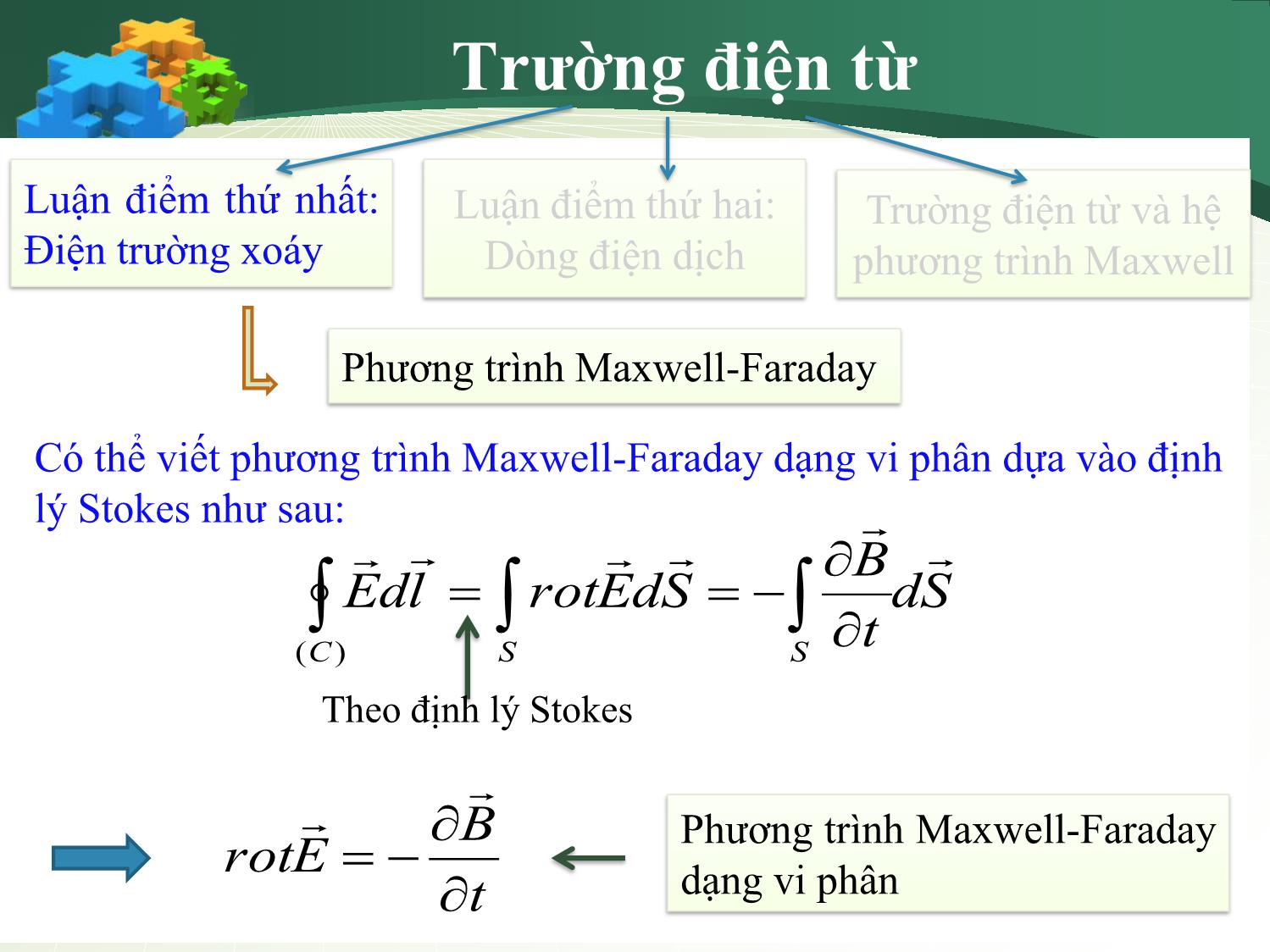
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ nhất 
 Phương trình Maxwell-Faraday 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ nhất 
 MọiPhương từ trườngtrình Maxwell biến thiên-Faraday theo thời gian đều xuất 
 hiện điện trường xoáy. 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ nhất 
 Phương trình Maxwell-Faraday 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phương trình Maxwell-Faraday 
Xét một mạch dẫn kín (C) đặt trong từ trường biến thiên. Sức điện 
động cảm ứng có thể xác định bằng hai cách sau: 
 d d 
  BdS  Edl
 c c 
 dt dt S (C)
 B Phương trình 
 Edl dS
 t Maxwell-Faraday 
 (C) S dạng tích phân 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phương trình Maxwell-Faraday 
Có thể viết phương trình Maxwell-Faraday dạng vi phân dựa vào định 
lý Stokes như sau: 
 B 
 Edl rotEdS dS
 (C) S S t
 Theo định lý Stokes 
 B Phương trình Maxwell-Faraday 
 rotE 
 t dạng vi phân 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ hai 
 Biểu thức của mật độ dòng điện dịch 
 Phương trình Maxwell-Ampere 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ hai 
 Biểu thức của mật độ dòng điện dịch 
 Phương trình Maxwell-Ampere 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ hai 
 Mọi điện trường biến thiên theo thời gian đều xuất hiện một từ 
 trường biến thiên 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ hai 
 Biểu thức của mật độ dòng điện dịch 
 Phương trình Maxwell-Ampere 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Biểu thức của mật độ dòng điện dịch 
Xét hai bản tụ điện có diện tích S và có tích điện tích mặt trên bề mặt 
bản tụ. Theo định lý Gauss ta có: 
 dD d Q
 DdS Q  
 dt dt S
 (S )
 dD 1 dQ idich
 dS jdich
 DdS dt S dt S
 (S )
 (S ) 
 dD
 - mật độ dòng điện dịch 
 D  jdich 
 dt
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phát biểu luận điểm thứ hai 
 Biểu thức của mật độ dòng điện dịch 
 Phương trình Maxwell-Ampere 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phương trình Maxwell-Ampere 
Theo như phần trên thì dòng điện toàn phần phải bao gồm dòng điện 
dẫn và dòng điện dịch. Như vậy định luât Ampere theo điều chỉnh của 
Maxwell sẽ như sau: 
 mà jtotal jdan jdich
 Hdl Itotal jtotaldS 
 D
 (l) (S ) và j E; j 
 dan dich t
 D 
 Hdl j dS - Phương trình Maxwell-
 dan Ampere dạng tích phân 
 (l) (S ) t 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Phương trình Maxwell-Ampere 
Có thể viết phương trình Maxwell-Faraday dạng vi phân dựa vào định 
lý Stokes như sau: 
 D 
 Hdl rotH.dS j dS
 dan t 
 (l) (S ) (S ) 
 Định lý Stokes Định luật Maxwell-Ampere 
 D
 rotH j - Phương trình Maxwell-
 dan t Ampere dạng vi phân 
 Ví dụ: mật độ dòng điện 
Điện trường trong một tụ điện phẳng có dạng E E0 sin(t)
với E0, tần số f, khoảng cách giữa hai bản d, điện dung của tụ 
điện C là các đại lượng đã biết. Tìm: 
1. Giá trị cực đại của dòng điện dịch. 
2. Độ dẫn điện. Biết giá trị cực đại của dòng điện dịch bằng một 
nửa giá trị cực đại dòng điện dẫn. 
 jdan E
 Cd 
 idich jdichS S 
   jdan
 0  
 D E
 j 
 dich t
 idichmax 0.5idanmax
 D 0E 
 jdichmax S 0.5 jdanmax S
 idichmax 2CdE0 f
 jdanmax 2 jdichmax
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Trường điện từ 
 Hệ phương trình Maxwell 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Trường điện từ 
 Hệ phương trình Maxwell 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Trường điện từ 
 Từ hai luận điểm nêu trên của Maxwell có thể đưa ra kết luận là từ 
 trường biến thiên làm xuất hiện điện trường biến thiên VÀ điện 
 trường biến thiên thì sinh ra từ trường biến thiên. Do đó mà trường 
 điện E và trường từ B lan truyền trong không gian dưới dạng sóng, 
 gọi là sóng điện từ. 
 Trường điện từ có mang năng lượng. 
 Trường điện từ 
 Sóng trường điện từ 
 Xét môi trường truyền sóng trong chân không hoặc điện môi. Q=0 
 Q .V 0. Độ dẫn điện  0.
  
 rot.rotE rotB
divD divD 0 t
 rot.rotE .divE 2E 2E
divB 0 
 D E
 rotB  .rotH 
 B 0 0  00
rotE t t
 t 2 1
 Đặt v 
 D D  00
rotH E rotH 
 t t 
 1 2E
 2E 0
 Phương trình truyền sóng cho điện trường v2 t 2
 1 2B
 Phương trình truyền sóng cho từ trường 2B 0
 v2 t 2
 Trường điện từ 
 1
Xét vận tốc truyền sóng v 
  00
 1 1 1
 3.108 m / s c
   1 1
 0 0 4 .10 7
 4 .9.109 9.1016
 c
Vậy v 
 
Trong đó c là vận tốc ánh sáng trong chân không. Như vậy ánh sáng 
cũng có tính chất điện từ. 
Đặt n  , n gọi là chiết suất tuyệt đối của môi trường. Do n>1 
nên vận tốc truyền sóng điện từ trong môi trường khác chân không có: 
 c c
 v c
  n
 Trường điện từ 
 Sóng điện từ đơn sắc phẳng 
Sóng điện từ được gọi là đơn sắc phẳng nếu thỏa mãn các điều kiện 
sau. 
1. Sóng điện từ là sóng ngang chỉ phụ thuộc vào một tọa độ. 
2. Cả điện trường và từ trường đều vuông góc với phương truyền sóng 
và tạo thành tam diện thuận như sau: 
 E H phuong truyen song 
3. Điện trường và từ trường dao động cùng pha, và trị số thỏa mãn 
phương trình: 
  0 E 0 H
 Ví dụ 1 
Cho biểu thức cảm ứng ứng từ của sóng điện từ đơn sắc phẳng: 
 B 3.10 8 cos 100 t 10 6 x (T)
 t đo bằng giây, x đo bằng m. Tìm biểu thức cường độ điện trường 
E của sóng điện từ đó. 
  0 E 0 H
 B
 B 0H H 
 0
 1
 3.108 m / s c
  00
 E 9cos 100 t 10 6 x (V/m)
 Ví dụ 2 
Vector cường độ điện trường của một trường điện từ có dạng: 
 8 
 E z,t 15cos 6 t 4 .10 z ex (T)
 t đo bằng giây, z đo bằng m. Tìm vector cường độ từ trường của 
sóng điện từ đó. 
 B 
 rotE dB rotE.dt
 t 
 B rotE.dt
 ex ey ez ex ey ez
      
 rotE 
 x y z x y z
 Ex Ey Ez Ex 0 0
 Ví dụ 2 
 ex ey ez
    Ex Ex 
rotE ex.0 ey 0 ez .0 e
 x y z z z y
 Ex 0 0
 E 
 B x .dt.e
 z y
 ( ) 4 .10 8 15sin 6 t 4 .10 8 z .dt.e
 y
 1 
 4 .10 8.15. ( )cos 6 t 4 .10 8 z e
 6 y
 7
 10 8 
 H cos 6 t 4 .10 z ey
 0
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Năng lượng trường điện từ W 
 E.D B.H
 W W W dV dV
 e m 
 V 2 V 2
 E.D B.H 
 dV wdV
 V 2 2 V
 E.D B.H
 w w w - Mật độ năng lượng trường điện từ 
 e m 2 2
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Công suất trường điện từ P 
 P E H.dS .dS
 S S
  E H - Mật độ công suất trường điện từ 
 Ví dụ: Công suất 
Coi rằng máy bức xạ sóng vô tuyến là chất điểm và sự hấp thụ 
năng lượng bởi môi trường là không đáng kể. Khi tăng khoảng 
cách trong liên lạc vô tuyến với tàu vũ trụ lên 4 lần thì công suất 
của máy phát cần phải tăng lên bao nhiêu lần? 
 P .dS S
 S
 2
P1 S1 4 r 2
 P2 4 4r 
 2 16
 2 P1 4 r
P2 S2 4 4r 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Trường điện từ 
 Hệ phương trình Maxwell 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Hệ phương trình Maxwell 
 Là hệ gồm 04 phương trình đặt trưng trường điện từ. Các phương 
 trình lần lượt là: 
 1. Định lý Gauss cho điện trường 
 2. Định lý Gauss cho từ trường 
 3. Định luật Maxwell-Faraday 
 4. Định luật Maxwell-Ampere 
 Hệ phương trình Maxwell có thể viết ở 02 dạng: 
 a. Tích phân 
 b. vi phân 
 Trường điện từ 
Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ 
Điện trường xoáy Dòng điện dịch phương trình Maxwell 
 Hệ phương trình Maxwell dạng: 
 Tích phân Vi phân 
 DdS Q 1. Gauss cho điện divD 
 (S )
 BdS 0 2. Gauss cho từ divB 0
 (S ) 
 B B
 Edl dS 3. Maxwell-Faraday rotE 
 t t
 (C) S 
 D D
 4. Maxwell-Ampere rotH E 
 Hdl E dS t
(l) (S ) t 
 Tổng kết chương 1 
 E.D B.H 
 dV wdV
 Năng lượng tđt W We Wm 
 V 2 2 V
 Mật độ 
 Công suất tđt P E H.dS .dS
 S S 
 Mật độ dòng điện D
 toàn phần jtotal jdan jdich trong đó jdan E; jdich 
 t
 Tích phân Hệ phương trình Maxwell dạng: Vi phân 
 DdS Q 1. Gauss cho điện divD 
 (S )
 BdS 0 2. Gauss cho từ divB 0
 (S ) 
 B
 B 3. Maxwell-Faraday rotE 
 Edl dS t
 (C) S t 
 D
 D 4. Maxwell-Ampere 
 Hdl j dS rotH jdan 
 dan t
(l) (S ) t 
 Tổng kết chương 1 
 B H 
 B  H  E H
 B 0
 rotE 
 t
 1 
E D W E.DdV
 D  E 2
 0 divD 
 1 
 H.BdV
 2
 D
 jdan E j 
 dich t
Sóng điện từ đơn sắc phẳng 
 0 E 0 H