Bài giảng Hình học Lớp 12 - Tiết 33: Vectơ và các phép toán vectơ trong không gian - Phạm Thị Ánh Hồng
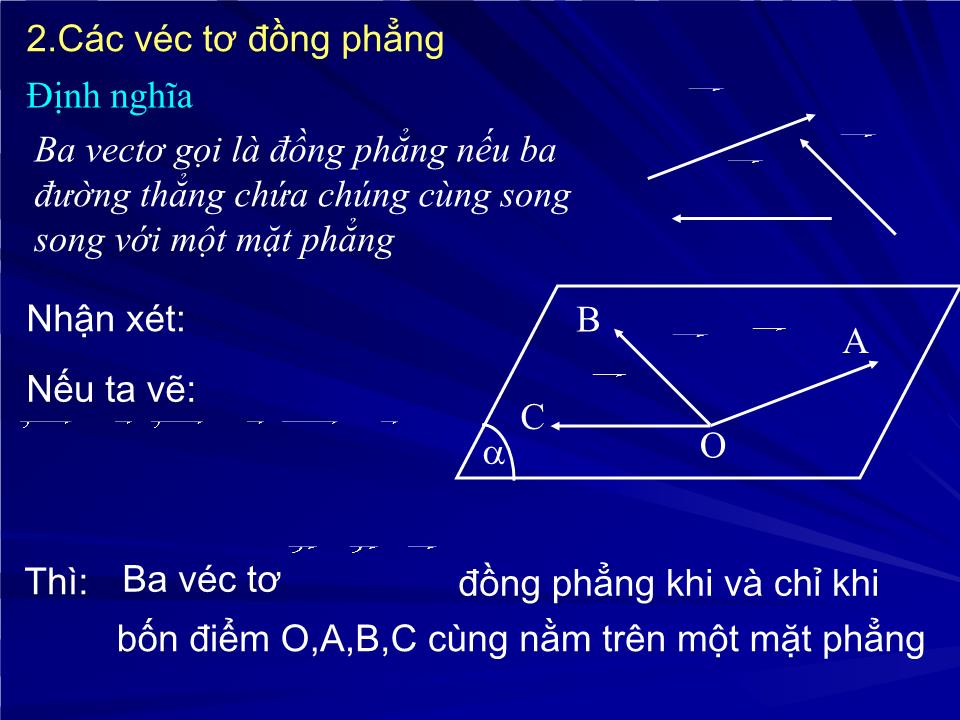
Định nghĩa
Ba vectơ gọi là đồng phẳng nếu ba đường thẳng chứa chúng cùng song song với một mặt phẳng
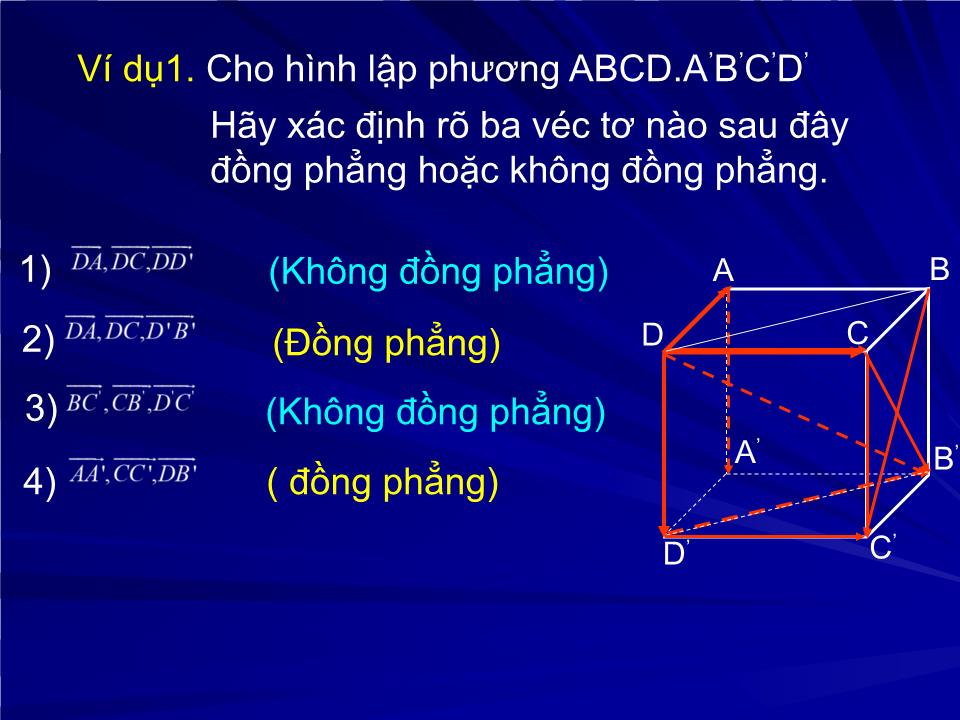
Ví dụ1. Cho hình lập phương ABCD.A’B’C’D’
Hãy xác định rõ ba véc tơ nào sau đây đồng phẳng hoặc không đồng phẳng.
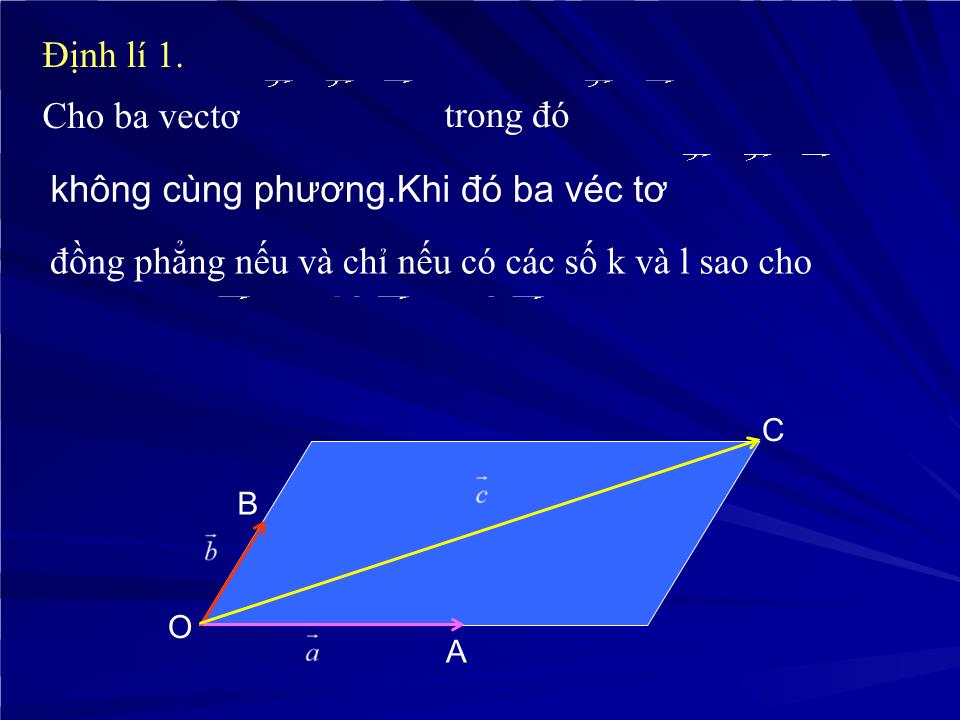
Định lí 1.
Cho ba vectơ
không cùng phương.Khi đó ba véc tơ
đồng phẳng nếu và chỉ nếu có các số k và l sao cho

Trang 1

Trang 2
Trang 3
Trang 4

Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 12 - Tiết 33: Vectơ và các phép toán vectơ trong không gian - Phạm Thị Ánh Hồng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Tiết 33: Vectơ và các phép toán vectơ trong không gian - Phạm Thị Ánh Hồng

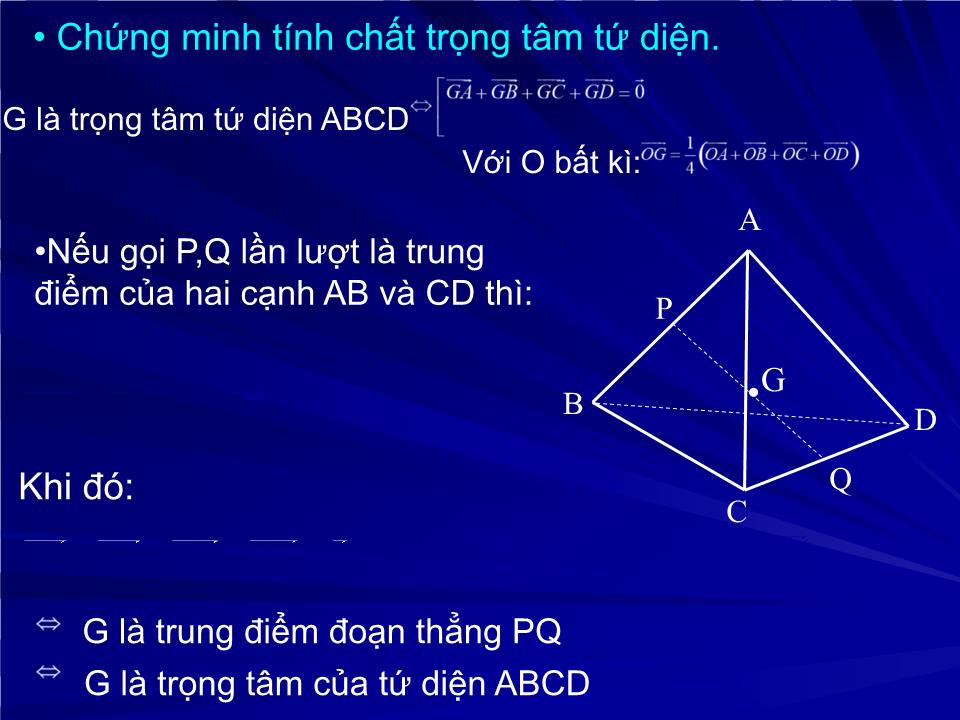
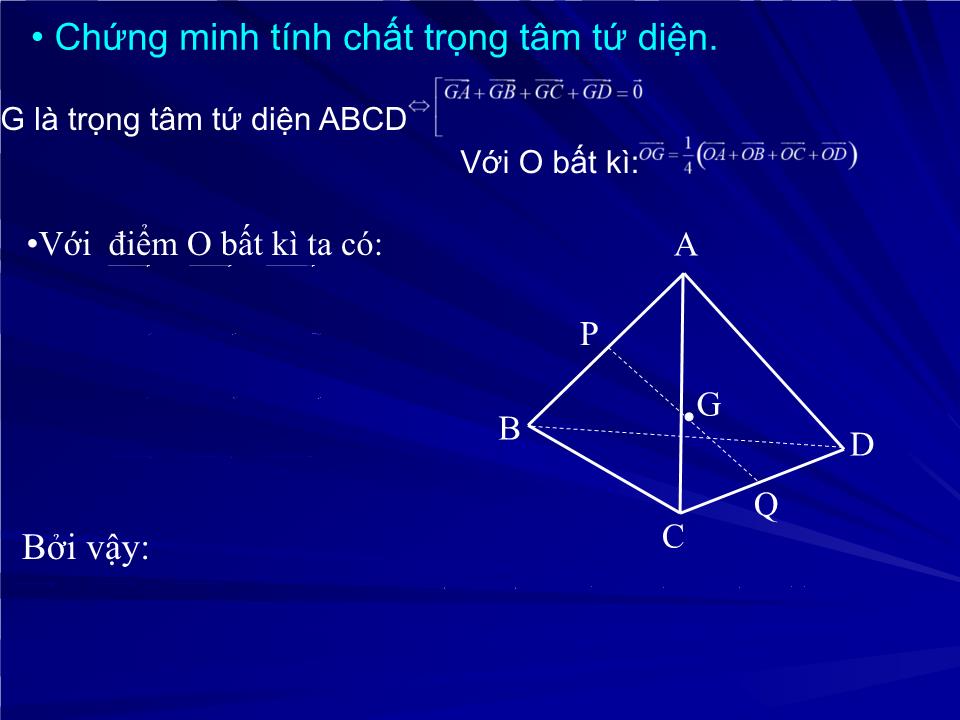
TRƯỜNG THPT CHU VĂN AN Bài giảng Hình học 12 Tiết 33 vectơ và các phép toán vectơ trong không gian NGƯỜI SoẠN: PHẠM THỊ Á NH H ỒNG TỔ TOÁN -TIN CHƯƠNG II PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN §1. V ECTƠ VÀ CÁC PHÉP TOÁN VECTƠ TRONG KHÔNG GIAN V E C T Ơ 2 VECTƠ CÙNG PHƯƠNG ĐỊNH NGHĨA VECTƠ 2 VECTƠ BẰNG NHAU VEC TƠ-KHÔNG 1.Vectơ trong không gian CÁC PHÉP TOÁN VECTƠ PHÉP TRỪ HAI VECTƠ PHÉP CỘNG CÁC VEC TƠ PHÉP NHÂN VÉC TƠ VỚI MỘT SỐ TÍCH VÔ HƯỚNG CỦA HAIVÉC TƠ một số tính chất quan trọng Qui tắc 3 điểm. Qui tắc hình bình hành. Nếu ABCD là hình bình hành thì: Tính chất trung điểm đoạn thẳng: G là trung điểm đoạn thẳng AB Tính chất trọng tâm tam giác: G là trọng tâm ∆ ABC Với ba điểm A,B,C bất kì luôn có: Với O bất kì: Với O bất kì: G là trọng tâm tứ diện ABCD Tính chất trọng tâm tứ diện. Với O bất kì: Nếu gọi P,Q lần lượt là trung điểm của hai cạnh AB và CD thì: Chứng minh tính chất trọng tâm tứ diện. G là trọng tâm tứ diện ABCD Với O bất kì: A B C D Q P G Khi đó: G là trung điểm đoạn thẳng PQ G là trọng tâm của tứ diện ABCD Với điểm O bất kì ta có: Bởi vậy: A B G C Q D P Chứng minh tính chất trọng tâm tứ diện. G là trọng tâm tứ diện ABCD Với O bất kì: Định nghĩa Ba vect ơ gọi là đồng phẳng nếu ba đ ư ờng thẳng chứa chúng cùng song song với một mặt phẳng C B O A 2.Các véc tơ đồng phẳng Nhận xét: Thì: đồng phẳng khi và chỉ khi bốn điểm O,A,B,C cùng nằm trên một mặt phẳng Ba véc tơ Nếu ta vẽ: Ví dụ1. Cho hình lập phương ABCD.A ’ B ’ C ’ D ’ Hãy xác định rõ ba véc tơ nào sau đây đồng phẳng hoặc không đồng phẳng. B C D A ’ B ’ C ’ D ’ A 1) 2) 3) 4) (Không đồng phẳng) (Đồng phẳng) (Không đồng phẳng) ( đồng phẳng) Định lí 1. Cho ba vect ơ trong đó không cùng phương.Khi đó ba véc tơ đồng phẳng nếu và chỉ nếu có các số k và l sao cho O A B C Định lí 2. Chứng minh: C X’ Từ O vẽ thì với mọi vect ơ ta đều có: Trong đó bộ 3 số k,l, m là duy nhất. Nếu ba vect ơ không đồng phẳng X B O A Vẽ XX’ song song (hoặc trùng) với OC cắt mp(OAB) tại X’ Ta có: Vì đồng phẳng, không cùng phương Từ (1),(2),(3) ta có: đồng phẳng Suy ra ( trái với giả thiết) Chứng minh tương tự ta cũng có l’ = l, m’ = m Vậy : k’ = k Nếu k’ k thì Vậy bộ ba số k,l,m là duy nhất. Chứng minh bộ ba số k,l,m là duy nhất. Nếu còn có bộ ba số k ’ , l ’ , m ’ sao cho: Thì: Ví dụ 2. Giải: A B D C A’ B’ D’ C’ N M Cho hình lập ph ươ ng ABCD.A’B’C’D’ cạnha. Gọi M, N lần l ư ợt là trung điểm của AD và BB’.Đặt a)Biểu diễn theo b)Chứng minh: MN A’C a) b)Ta có: .Nh ư vậy: MN A’C BÀI TẬP VỀ NHÀ Bài 1, 2, 4, 6, 7 (SGK trang 59) Xin chân thành cảm ơn sự chú ý theo dõi của các thày giáo, cô giáo và các em học sinh!
File đính kèm:
 bai_giang_hinh_hoc_lop_12_tiet_33_vecto_va_cac_phep_toan_vec.ppt
bai_giang_hinh_hoc_lop_12_tiet_33_vecto_va_cac_phep_toan_vec.ppt

