Bài giảng Hình học Lớp 12 - Chương 3 - Tiết 91: Hệ tọa độ trong không gian

CHÀO MỪNG CÁC THẦY CÔ GIÁO VỀ DỰ GIẢNG 
MÔN TOÁN - LỚP 12 
Giáo viên: Chu Thị Luyến 
Trung tâm GDTX – HN – DN Chí Linh 
KIỂM TRA BÀI CŨ 
Câu 1: 
Trong không gian Oxyz, cho: 
 I(a; b; c), 
M(x; y; z) 
Tính độ dài đoạn thẳng IM. 
Câu 2: Nêu định nghĩa 
 mặt cầu (S) tâm I bán kính r. 
KIỂM TRA BÀI CŨ 
S(I; r) = {M | IM = r} 
. 
I 
r 
(S) 
. 
M 
z 
x 
y 
O . 
. 
I 
r 
. 
M 
(S) 
b 
a 
c 
(a; b; c) 
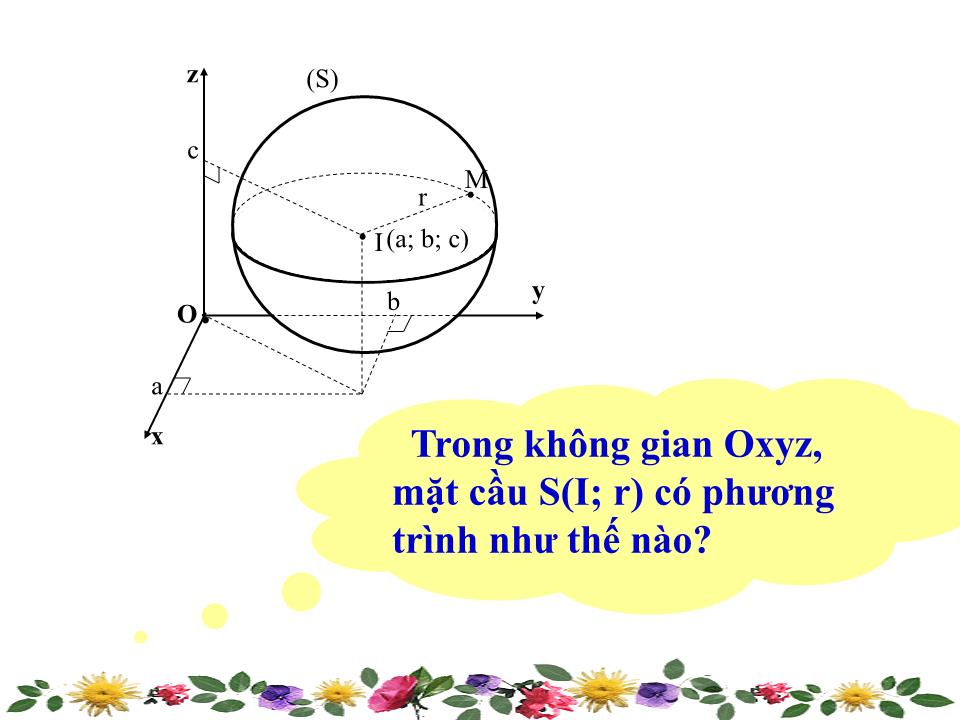
 Trong không gian Oxyz, mặt cầu S(I; r) có ph ươ ng trình nh ư thế nào? 
TIẾT 91: 
(Tiết 2) 
HỆ TỌA ĐỘ TRONG KHÔNG GIAN 
z 
x 
y 
O . 
. 
I 
r 
. 
M 
(S) 
b 
a 
c 
(a; b; c) 
(x; y; z) 
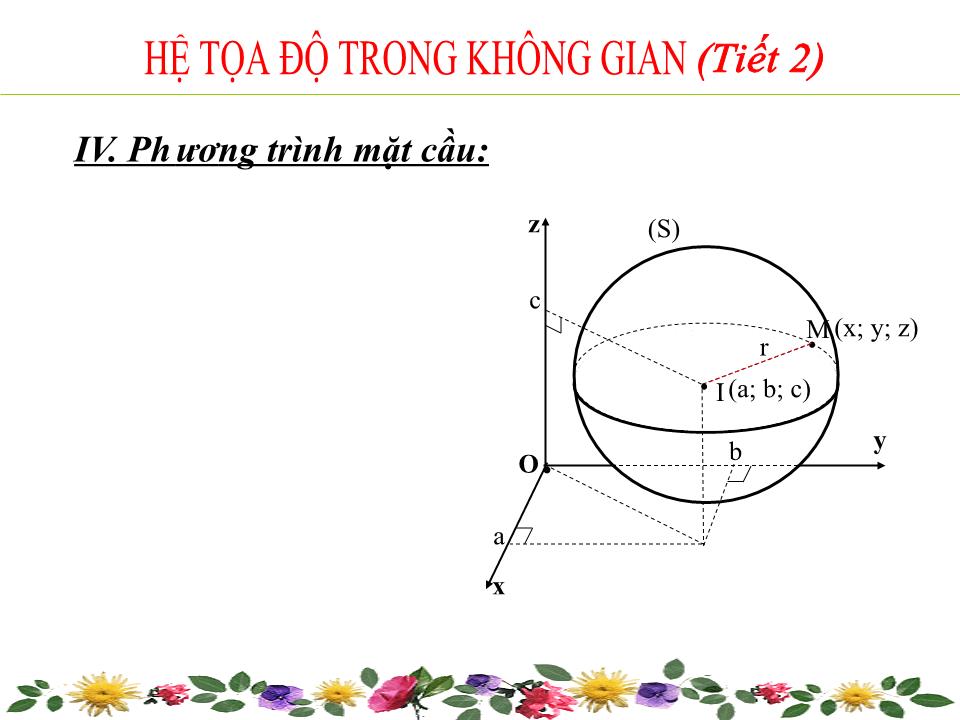
IV. Ph ươ ng trình mặt cầu: 
HỆ TỌA ĐỘ TRONG KHÔNG GIAN 
(Tiết 2) 
. 
I 
r 
. 
M 
(S) 
(a; b; c) 
(x; y; z) 
b 
a 
c 
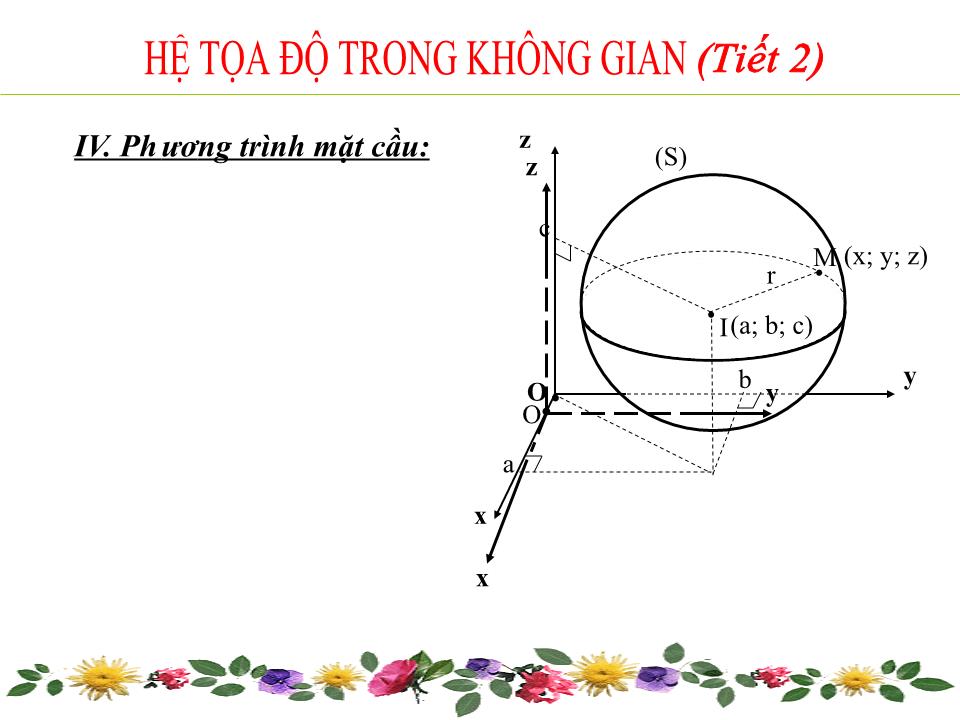
IV. Ph ươ ng trình mặt cầu: 
z 
x 
y 
O . 
O 
z 
 . 
y 
x 
HỆ TỌA ĐỘ TRONG KHÔNG GIAN 
(Tiết 2) 
Hoạt động 4: 
Viết ph ươ ng trình mặt cầu tâm I(1; -2; 3) có bán kính r = 5. 
Để lập ph ươ ng trình mặt cầu, cần xác định 2 yếu tố: 
 1. Tâm mặt cầu I(a; b; c). 
 2. Bán kính r của mặt cầu. 
 Kết luận ph ươ ng trình mặt cầu là: 
 (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
Ví dụ 1: 
 Trong các ph ươ ng trình sau, ph ươ ng trình nào là ph ươ ng trình mặt cầu? Nếu là ph ươ ng trình mặt cầu, hãy xác định tọa độ tâm và bán kính? 
 a) (x+1) 2 + (y+2) 2 + (z-3) 2 = 3 (1a) 
 b) (x+1) 2 + (y-1) 2 + (z+2) 2 = -10 (1b) 
 c) (x-2) 2 + (y+1) 2 + (2z + 1) 2 = 4. (1c) 
 Ví dụ 1: Trong các ph ươ ng trình sau, ph ươ ng trình nào là ph ươ ng trình mặt cầu? Nếu là ph ươ ng trình mặt cầu, hãy xác định tọa độ tâm và bán kính? 
 a) (x+1) 2 + (y+2) 2 + (z-3) 2 = 3 (1a) 
Ph ươ ng trình (1a) là ph ươ ng trình mặt cầu 
Để lập ph ươ ng trình mặt cầu, cần xác định 2 yếu tố: 
 1. Tâm mặt cầu I(a; b; c). 
 2. Bán kính r của mặt cầu. 
 Kết luận ph ươ ng trình mặt cầu là: 
 (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
+) Tâm I 
(-1; -2; 3) 
+) Bán kính r = 
 b) (x+1) 2 + (y-1) 2 + (z+2) 2 = -10 (1b) 
Ph ươ ng trình (1b) không là ph ươ ng trình mặt cầu 
Để lập ph ươ ng trình mặt cầu, cần xác định 2 yếu tố: 
 1. Tâm mặt cầu I(a; b; c). 
 2. Bán kính r của mặt cầu. 
 Kết luận ph ươ ng trình mặt cầu là: 
 (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
Vì: r 2 = -10 < 0 (vô lí). 
 Ví dụ 1: Trong các ph ươ ng trình sau, ph ươ ng trình nào là ph ươ ng trình mặt cầu? Nếu là ph ươ ng trình mặt cầu, hãy xác định tọa độ tâm và bán kính? 
 c) (x-2) 2 + (y+1) 2 + ( z + 1) 2 = 4 (1c) 
Ph ươ ng trình (1c) không là ph ươ ng trình mặt cầu 
Để lập ph ươ ng trình mặt cầu, cần xác định 2 yếu tố: 
 1. Tâm mặt cầu I(a; b; c). 
 2. Bán kính r của mặt cầu. 
 Kết luận ph ươ ng trình mặt cầu là: 
 (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
 Vì hệ số của z trong ngoặc bằng 2, hệ số của x,y trong 
 ngoặc bằng 1. 
 Ví dụ 1: Trong các ph ươ ng trình sau, ph ươ ng trình nào là ph ươ ng trình mặt cầu? Nếu là ph ươ ng trình mặt cầu, hãy xác định tọa độ tâm và bán kính? 
2 
(x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
(d = a 2 + b 2 + c 2 - r 2 ) 
Xét mặt cầu S(I; r): 
x 2 
+ z 2 – 2cz + c 2 
 – 2ax 
+ a 2 
 + y 2 – 2by + b 2 
 = r 2 
+ d = 0 
x 2 + y 2 + z 2 
– 2ax – 2by - 2cz 
x 2 + y 2 + z 2 – 2ax – 2by -2cz + d = 0 (1’) 
Ph ươ ng trình: 
x 2 + y 2 + z 2 + 2Ax + 2By + 2Cz + D = 0 (2) 
là ph ươ ng trình mặt cầu với điều kiện nào? 
Ph ươ ng trình: 
x 2 + y 2 + z 2 + 2Ax + 2By + 2Cz + D = 0 (2) 
là ph ươ ng trình mặt cầu với điều kiện nào? 
(2) (x+A) 2 + (y+B) 2 + (z+C) 2 = A 2 + B 2 + C 2 – D (2’) 
Ví dụ 2: 
 Ph ươ ng trình sau có là ph ươ ng trình mặt cầu không? Nếu là ph ươ ng trình mặt cầu hãy xác định tọa độ tâm và bán kính? 
 x 2 + y 2 + z 2 – 2x + 4y – 8z + 21 = 0 (2a) 
b) x 2 + 2y 2 + z 2 + 6x – 4y + 2z – 1 = 0 (2b) 
c) 2x 2 + 2y 2 + 2z 2 – 4x + 8y – 4z + 10 = 0 (2c) 
Ví dụ 2: 
x 2 + y 2 + z 2 – 2x + 4y – 8z + 21 = 0 (2a) 
Vậy ph ươ ng trình (2a) không là ph ươ ng trình mặt cầu. 
Ta có: 
2A = -2 
2B = 4 
2C = -8 
D = 21 
A = -1 
B = 2 
C = -4 
0 
 A 2 + B 2 + C 2 – D = 
Lời giải: 
Ví dụ 2: 
b) x 2 + 2y 2 + z 2 + 6x – 4y + 2z – 1 = 0 (2b) 
Ph ươ ng trình (2b) không là ph ươ ng trình mặt cầu. 
Vì: hệ số của x 2 , y 2 , z 2 khác nhau. 
c) 2x 2 + 2y 2 + 2z 2 – 4x + 8y – 4z + 10 = 0 (2c) 
x 2 + y 2 + z 2 – 2x + 4y – 2z + 5 = 0. 
A = 
-1 
2 
-1 
5 
1 
> 0 
Vậy ph ươ ng trình (2c) là ph ươ ng trình mặt cầu có: 
C = 
; 
; 
+) Tâm I 
(1; -2; 1) 
+) Bán kính r = 
 A 2 + B 2 + C 2 – D = 
Lời giải: 
B = 
D = 
Ví dụ 3: 
Xác định tâm và bán kính của mặt cầu có ph ươ ng trình: 
x 2 + y 2 + z 2 + 4x – 2y + 6z + 5 = 0 (**) 
(2) 
(1) 
Ví dụ 3: 
Xác định tâm và bán kính của mặt cầu có ph ươ ng trình: 
x 2 + y 2 + z 2 + 4x – 2y + 6z + 5 = 0 (**) 
Lời giải: 
Ta có: A = 
 B = 
 C = 
 D = 
2 
-1 
3 
5 
 Tâm I 
(-2; 1; -3) 
Bán kính r = 
3 
20 
Cách 2: 
Tính A 2 + B 2 + C 2 – D = 
9 
Ví dụ 3: 
Xác định tâm và bán kính của mặt cầu có ph ươ ng trình: 
x 2 + y 2 + z 2 + 4x – 2y + 6z + 5 = 0 (**) 
Lời giải: 
(**) ( x+2) 2 
 Tâm I 
(-2; 1; -3) 
Bán kính r = 
3 
 + (y-1) 2 
 + (z+3) 2 
 = 9 
Cách 2: 
+ Cách 1 : 1. Xác định các hệ số A, B, C, D. 
 2. Tính A 2 + B 2 + C 2 - D 
 3. Kết luận: Tâm I(-A; -B; -C), 
 Bán kính r = 
 Để tìm tâm và bán kính của mặt cầu (S), ta thực hiện 
một trong hai cách sau: 
 Cho mặt cầu S(I; r): 
 x 2 + y 2 + z 2 + 2Ax + 2By + 2Cz + D = 0 (2) 
 (A 2 + B 2 + C 2 – D > 0) 
+ Cách 2 : Biến đổi ph ươ ng trình (2) về dạng ph ươ ng trình:  (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
 Kết luận: Tâm I(a; b; c) 
 Bán kính r. 
Cách lập ph ươ ng trình mặt cầu: 
 1. Tìm tâm I(a; b; c) . 
 2. Tìm bán kính r ( r > 0 ). 
 Kết luận: 
 S(I; r): (x-a) 2 + (y-b) 2 + (z-c) 2 = r 2 (1) 
2. Ph ươ ng trình: x 2 + y 2 + z 2 + 2Ax + 2By + 2Cz + D = 0 (2) 
 là ph ươ ng trình mặt cầu với điều kiện A 2 + B 2 + C 2 – D > 0 . 
 Khi đó mặt cầu có: 
 + Tâm I(-A; -B; -C) 
 + Bán kính r = 
CỦNG CỐ 
5. Ph ươ ng trình mặt cầu. 
CỦNG CỐ 
Trong không gian Oxyz: 
 Các em về nhà học bài và làm bài tập 5,6 trong SGK/Tr68. 
HƯỚNG DẪN 
Gợi ý: 
 Bài 5: Làm t ươ ng tự ví dụ 2 và ví dụ 3. 
. 
I 
r 
. 
B 
A . 
Bài 6: 
 a) Viết ph ươ ng trình mặt cầu đ ư ờng kính AB. 
HƯỚNG DẪN 
. 
C 
r 
. 
A 
Bài 6: 
 b) Viết ph ươ ng trình mặt cầu đi qua điểm A và có tâm C. 
HƯỚNG DẪN