Bài giảng Hình học Lớp 12 - Chương 3 - Tiết 37, Bài 3: Phương trình đường thẳng trong không gian

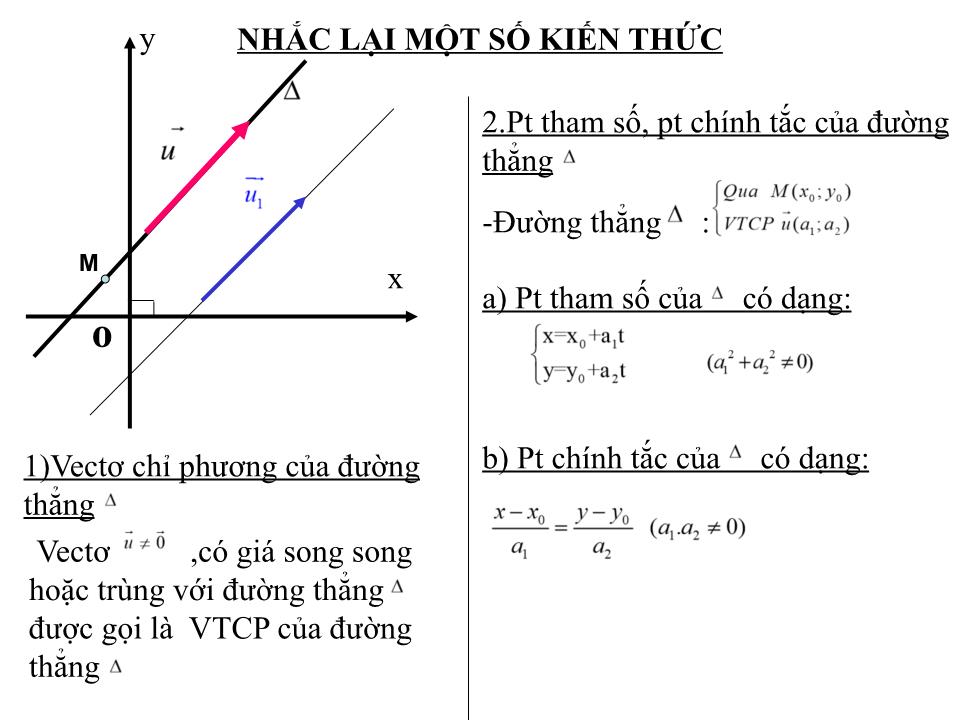
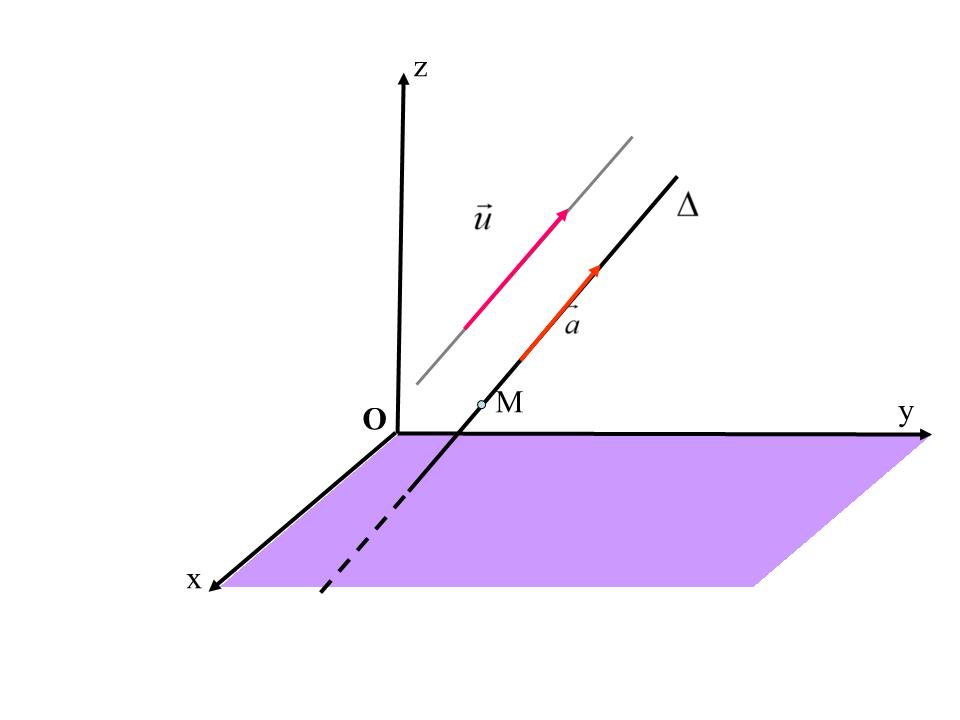
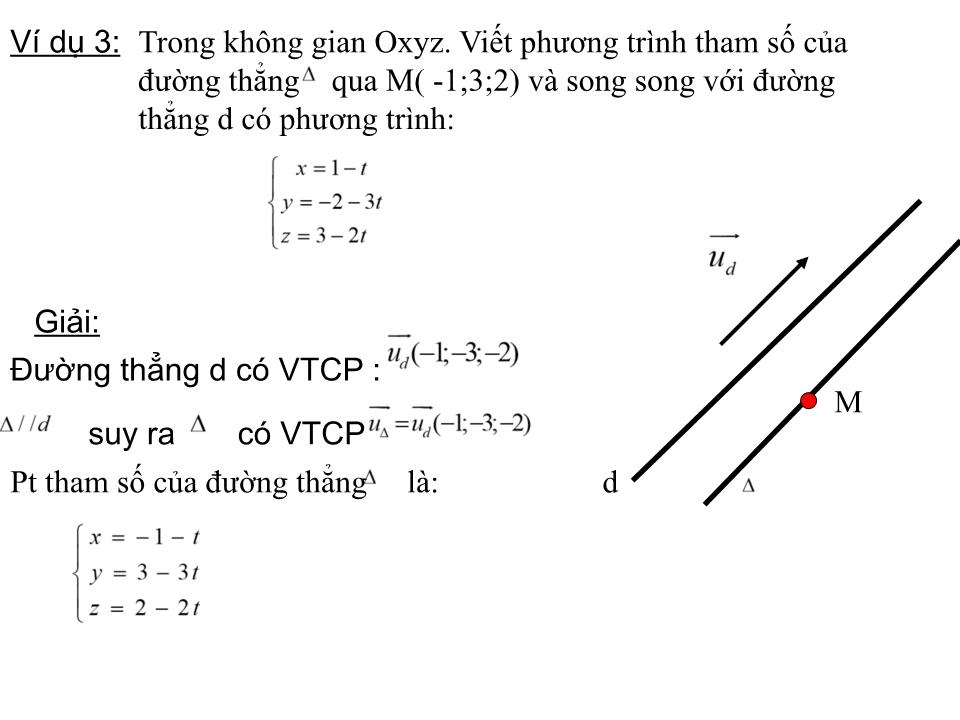
BÀI DẠY: 
§3 PHƯƠNG TRÌNH ĐƯỜNG THẲNG 
 TRONG KHÔNG GIAN 
 (TIẾT 37) 
NHẮC LẠI MỘT SỐ KIẾN THỨC 
 Vectơ ,có giá song song hoặc trùng với đường thẳng được gọi là VTCP của đường thẳng 
1)Vectơ chỉ phương của đường thẳng 
x 
o 
y 
M 
 -Đường thẳng : 
a) Pt tham số của có dạng: 
2.Pt tham số, pt chính tắc của đường thẳng 
b) Pt chính tắc của có dạng: 
O 
y 
z 
x 
M 
I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG: 
y 
z 
x 
M 0 
0 
M 
CM: 
Ta có: 
cùng phương với 
1. Định lý: 
Trong không gian Oxyz cho 
đường thẳng đi qua M(x 0 ;y 0 ;z 0 ) 
 nhận làm vectơ chỉ 
phương. Điều kiện cần và đủ để 
điểm M ( x; y; z ) nằm trên là có 
một số thực t sao cho: 
I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG 
trong đó t là tham số. 
Định nghĩa: 
Phương trình tham số của đường thẳng đi qua điểm 
M(x 0 ;y 0 ; z 0 ) và có vectơ chỉ phương là phương 
trình có dạng: 
Chú ý: 
Nếu đều khác 0 ta còn viết pt của đường thẳng dưới dạng chính tắc như sau: 
Đường thẳng : 
Pt chính tắc của : 
Ví dụ 1: Trong không gian Oxyz .Viết pt tham số, pt chính tắc của đường thẳng đi qua điểm M(1;-2;3) và có vectơ chỉ phương 
Giải: 
Pt tham số của : 
Pt chính tắc của : 
Pt tham số của đường thẳng là: 
Ví dụ 2: Trong không gian Oxyz cho hai điểm A(1; -2; 3) và 
 B(3; 1; 1). Viết phương trình tham số của đường thẳng AB. 
Giải 
Đường thẳng AB có VTCP là 
Pt tham số của đường thẳng AB là: 
Đường thẳng : 
Pt tham số của : 
A 
B 
Đường thẳng d có VTCP : 
suy ra có VTCP 
Pt tham số của đường thẳng là: 
M 
d 
Ví dụ 3: 
Giải: 
Trong không gian Oxyz. Viết phương trình tham số của đường thẳng qua M( -1;3;2) và song song với đường thẳng d có phương trình: 
Giải: 
VD4 : Trong không gian Oxyz cho đường thẳng có phương trình tham số: 
Hãy tìm tọa độ một điểm M trên và một vectơ chỉ phương của 
Chú ý: 
Trong không gian Oxyz cho đường thẳng có pt tham số: 
Với mỗi điểm M tùy ý thuộc thì 
Đường thẳng đi qua M(3;1;2) và một VTCP của là 
a) Ta có: mp(P) có VTPT 
Vì nên có VTCP 
Pt tham số của đường thẳng là : 
Giải 
Ví dụ 5: 
Trong không gian Oxyz cho (P): 2 x + 4 y + z + 9 = 0.và điểm A(1; -2; 3) 
a.Viết pt tham số của đường thẳng đi qua A và vuông góc với mp(P). 
b.Tìm tọa độ hình chiếu H của A lên mp(P). 
P ) 
A 
Gọi H (1+2t;-2+4t;3+t) là hình chiếu của A lên (P). 
Ta có 
H 
2(1+2t) + 4 (-2+4t) + 3+t + 9 = 0 
b) 
Gọi H(3-2t;1+t;2-t) là hình chiếu của A lên . 
VD6 : Trong không gian Oxyz cho điểm A(2;3;1)và đường thẳng có phương trình tham số: 
Tìm tọa độ hình hình chiếu H của A lên 
Giải 
 , có VTCP 
Ta có: 
A 
H 
Vì H là hình chiếu của A lên nên: 
Củng cố: 
Pt tham số của : 
Đường thẳng : 
1) 
 Trong không gian Oxyz cho đường thẳng có pt tham số: 
Với mỗi điểm M tùy ý thuộc thì 
2) 
(với ) 
Pt chính tắc của : 
1)Trong không gian Oxyz cho đường thẳng d đi qua M(3;2;-2) và 
có VTCP pt tham số của đường thẳng d là: 
C 
A 
D 
B 
 Bài tập trắc nghiệm: 
2)Trong không gian Oxyz cho đường thẳng d đi qua M(3;4;-2) và 
vuông góc với mp(Q):3x-4y-z+2=0 .Phương trình tham số của 
đường thẳng d là: 
C 
D 
B 
A