Bài giảng Hình học Lớp 12 - Chương 3 - Tiết 35, Bài 3: Phương trình đường thẳng trong không gian - Nguyễn Hoàng Yến Phượng
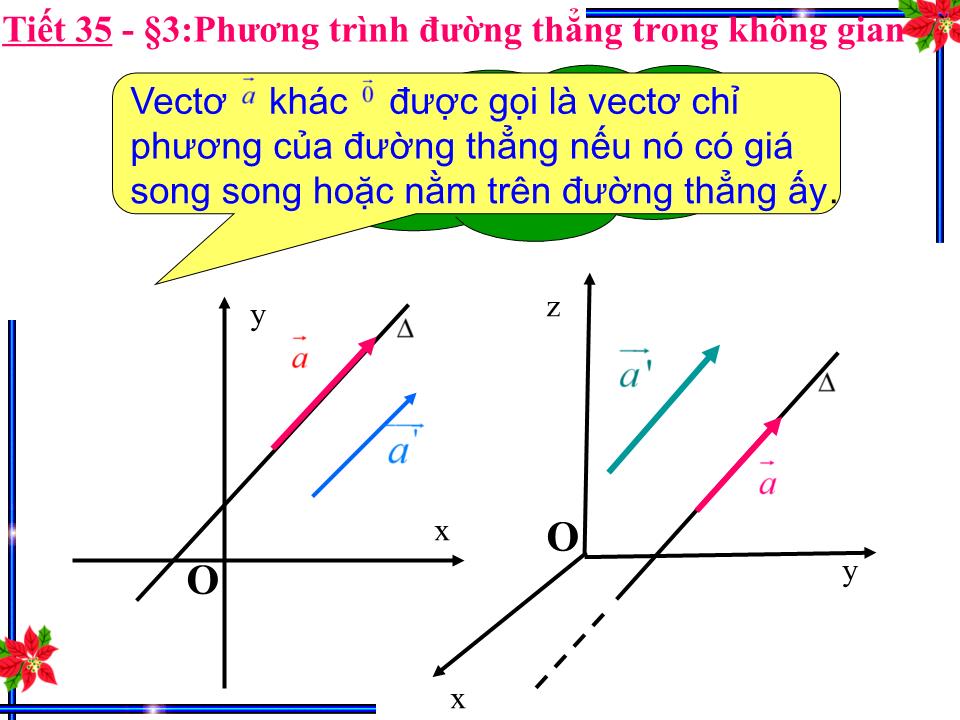
Vectơ khác được gọi là vectơ chỉ phương của đường thẳng nếu nó có giá song song hoặc nằm trên đường thẳng ấy.
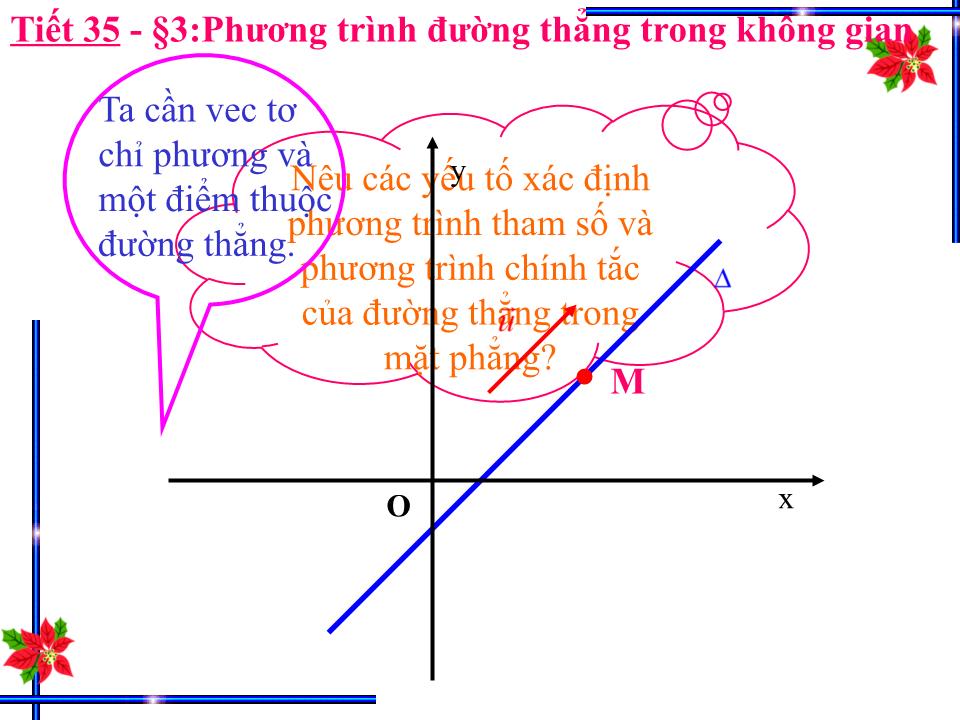
Ta cần vec tơ chỉ phương và một điểm thuộc đường thẳng.
Nêu các yếu tố xác định phương trình tham số và phương trình chính tắc của đường thẳng trong mặt phẳng?
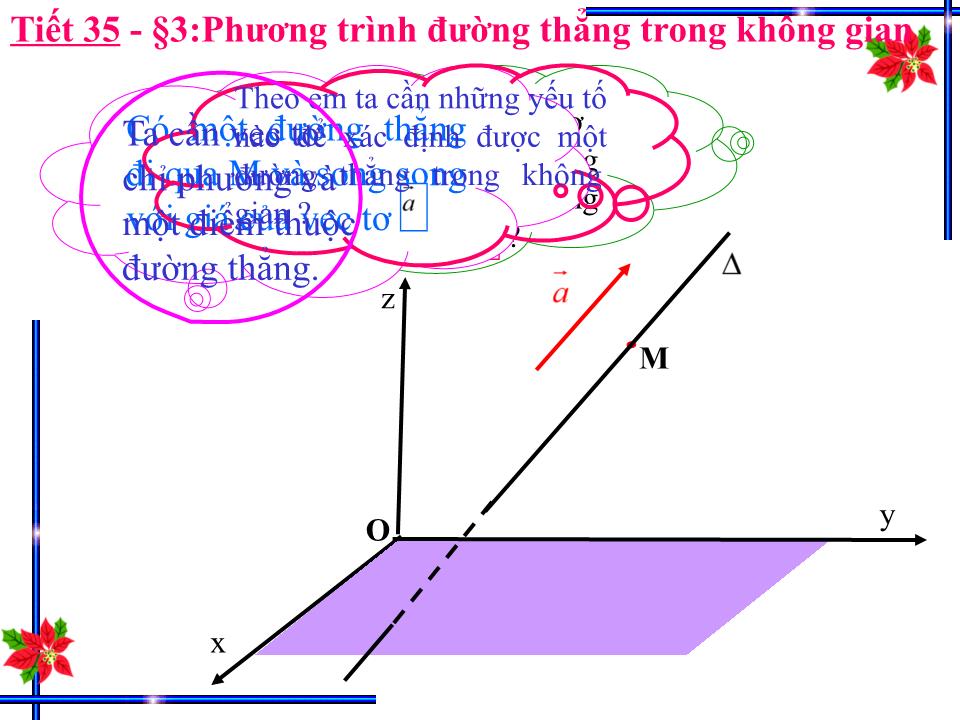
Theo em ta cần những yếu tố nào để xác định được một ñường thẳng trong không gian ?
Ta cần vec tơ chỉ phương và một điểm thuộc đường thẳng.
Có một đường thẳng đi qua M và song song với giá của vec tơ
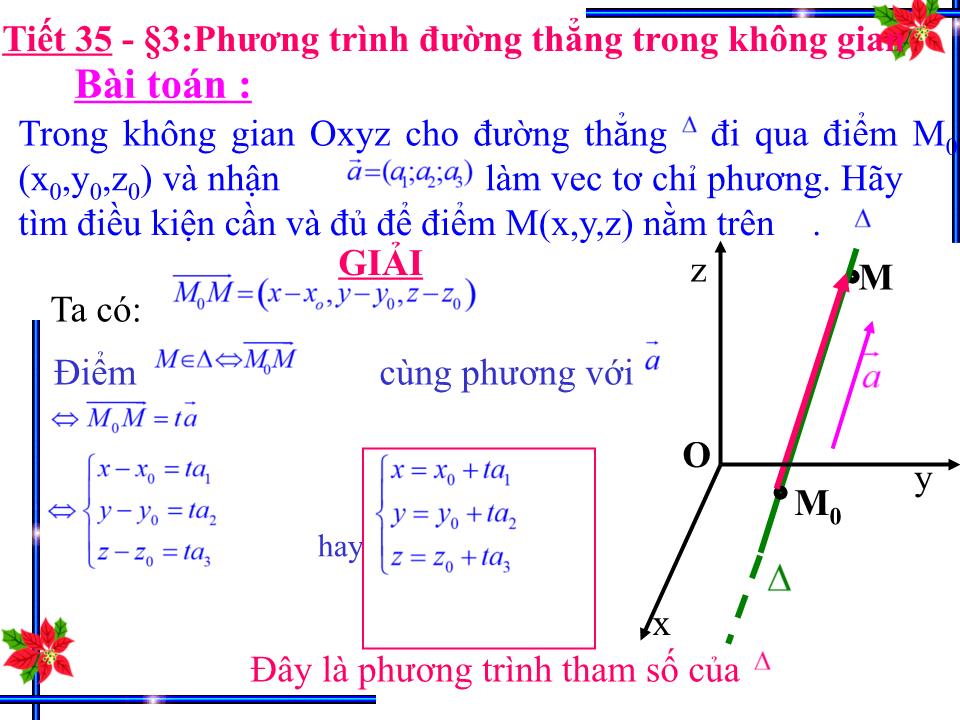
Bài toán :
Trong không gian Oxyz cho đường thẳng đi qua điểm M0(x0,y0,z0) và nhận làm vec tơ chỉ phương. Hãy tìm điều kiện cần và đủ để điểm M(x,y,z) nằm trên .

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 12 - Chương 3 - Tiết 35, Bài 3: Phương trình đường thẳng trong không gian - Nguyễn Hoàng Yến Phượng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 3 - Tiết 35, Bài 3: Phương trình đường thẳng trong không gian - Nguyễn Hoàng Yến Phượng

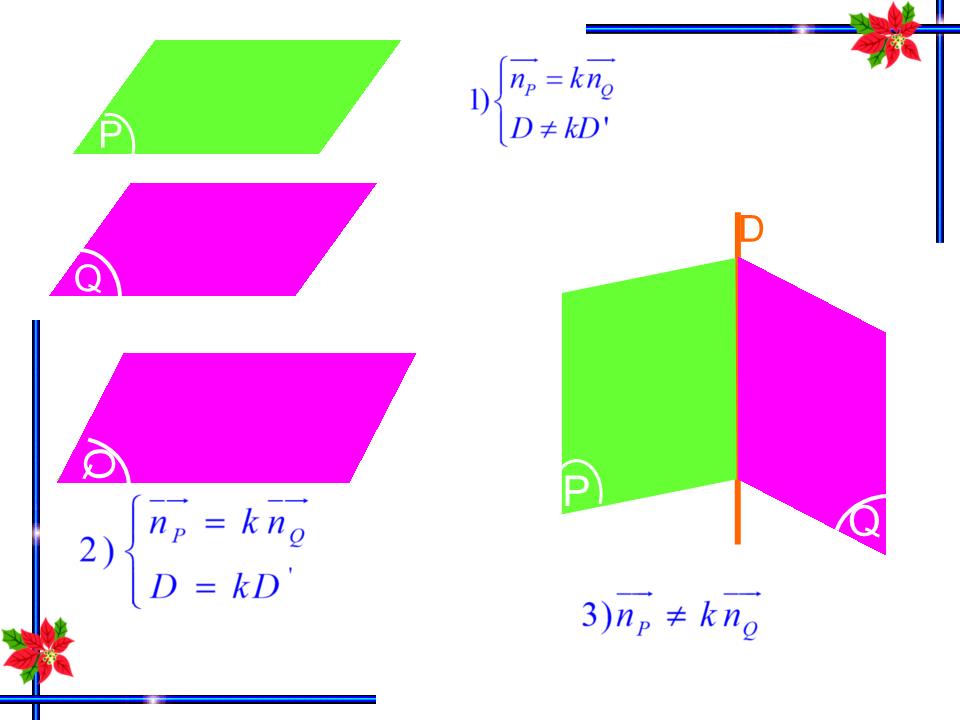
KÍNH CHÀO QUÝ THẦY CÔ VỀ DỰ GIỜ LỚP 12C4 SỞ GIÁO DỤC – ĐÀO TẠO KHÁNH HOÀ TRƯỜNG T.H.P.T NGUYỄN THỊ MINH KHAI GV: NGUYỄN HOÀNG YẾN PH Ư ỢNG (P) : Ax + By + Cz + D = 0 Với A 2 +B 2 +C 2 0 (Q) :A’x +B’y +C’z +D’ = 0 Với A’ 2 +B’ 2 +C’ 2 0 Xét vị trí tương đối của hai mặt phẳng? Cho hai mặt phẳng Trong không gian, hai mặt phẳng có ba vị trí tương đối: KIỂM TRA BÀI CŨ Đáp án: D Q P P P Q Q KIỂM TRA BÀI CŨ Câu hỏi thêm : 1/Nhắc lại phương trình tham số của đường thẳng trong mặt phẳng Oxy ? 1/ Phương trình tham số: Đáp án: trong đó là VTCP 2/ Điểm M(2,-3) và vec tơ chỉ phương = (-1,2) 2/ Tìm một vec tơ chỉ phương và một điểm M thuộc đường thẳng có phương trình tham số: Tiết 35 - § 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN I . Phương trình tham số của đường thẳng II. Điều kiện để hai đường thẳng song song , cắt nhau , chéo nhau Giải các bài toán liên quan đến phương trình đường thẳng Cầu sông Hàn tp Đà Nẵng Cầu Tràng Tiền – Huế Cầu Hàm Rồng –Thanh Hoùa Cầu Nguyễn Văn Trỗi - Nguyễn Thị Lý – Đà Nẵng Cầu Nhật Tân – Hà Nội O x y z y x O Hãy nhắc lại định nghĩa vectơ chỉ phương của đường thẳng ? Vectơ khác được gọi là vectơ chỉ phương của đường thẳng nếu nó có giá song song hoặc nằm trên đường thẳng ấy . Tiết 35 - §3:Phương trình đường thẳng trong không gian Nêu các yếu tố xác định phương trình tham số và phương trình chính tắc của đường thẳng trong mặt phẳng? O x y M Ta cần vec tơ chỉ phương và một điểm thuộc đường thẳng. Tiết 35 - §3:Phương trình đường thẳng trong không gian O x y z Tiết 35 - §3:Phương trình đường thẳng trong không gian Trong không gian cho vectơ , có bao nhiêu đường thẳng đi qua M và song song với giá của vec tơ ? Có một đường thẳng đi qua M và song song với giá của vec tơ Theo em ta cần những yếu tố nào để xác định được một ñ ường thẳng trong không gian ? Ta cần vec tơ chỉ phương và một điểm thuộc đường thẳng. M Bài toán : GIẢI Điểm cùng phương với hay x y z O M 0 M Ta có: Trong không gian Oxyz cho đường thẳng đi qua điểm M 0 (x 0 ,y 0 ,z 0 ) và nhận làm vec tơ chỉ phương. Hãy tìm điều kiện cần và đủ để điểm M(x,y,z) nằm trên . Đây là phương trình tham số của Tiết 35 - §3:Phương trình đường thẳng trong không gian Tiết 35 : - § 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN Trong không gian Oxyz cho đường thẳng đi qua nhận làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M ( x; y; z ) nằm trên là có một số thực t sao cho : I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG: 1. Định lý Tiết 35 : - § 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN Phương trình tham số của đường thẳng đi qua điểm và có vectơ chỉ phương có dạng: I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG: 2. Định nghĩa 1. Định lý với t : tham số I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Ví dụ 1 : Viết phương trình tham số của đường thẳng đi qua điểm M(1,-2,3) và có vectơ chỉ phương = (2;3; -4) Thì ph ươ ng trình tham số : x = x o + a 1 t y = y o + a 2 t z = z o + a 3 t ( t là tham số) Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng = ( a 1 ;a 2 ;a 3 ) Giải Phương trình tham số của đường thẳng là: Tiết 35 - §3:Phương trình đường thẳng trong không gian I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Ví dụ 2 : Viết phương trình tham số của đường thẳng AB với A(1; -4 ;3) và B (2; 0; 0) Thì ph ươ ng trình tham số : x = x o + a 1 t y = y o + a 2 t z = z o + a 3 t ( t là tham số) Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng = ( a 1 ;a 2 ;a 3 ) Giải: Phương trình tham số của đường thẳng AB là: Đường thẳng AB có vectơ chỉ phương = ( 1; 4 ; - 3) Tiết 35 - §3:Phương trình đường thẳng trong không gian A B I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Phiếu học tập 1: Giải: Đây chính là phương trình chính tắc của đường thẳng Thì ph ươ ng trình tham số : x = x o + a 1 t y = y o + a 2 t z = z o + a 3 t ( t là tham số) Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng = ( a 1 ;a 2 ;a 3 ) Từ phương trình tham số khử t , ta được : Tiết 35 - §3:Phương trình đường thẳng trong không gian Từ phương trình tham số của đường thẳng với a 1 , a 2 , a 3 đều khác 0 hãy biểu diễn t theo x,y,z ? I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Thì ph ươ ng trình tham số : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) Tiết 35 - §3:Phương trình đường thẳng trong không gian ( t: tham số) Phương trình chính tắc : Ví dụ 3 : Viết phương trình chính tắc của đường thẳng đi qua A(1; -2; 0) và vuông góc với mặt phẳng (P): 2 x - 4 y + 6 z + 9 = 0. Giải: P ) Mặt phẳng (P) có vtpt là Phương trình chính tắc của : Vì nên VTCP của là: I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Thì ph ươ ng trình tham số : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) Tiết 35 - §3:Phương trình đường thẳng trong không gian ( t: tham số) Phương trình chính tắc : Phiếu học tập 2: Cho đường thẳng d có phương trình tham số: a) Hãy tìm một vec tơ chỉ phương và một điểm thuộc đường thẳng trên b) Hãy viết phương trình chính tắc của đường thẳng d. a) Đường thẳng d đi qua điểm M(-5,3,1) và có vtcp Giải: b) Đường thẳng d có phương trình chính tắc là : I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Thì ph ươ ng trình tham số : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) Tiết 35 - §3:Phương trình đường thẳng trong không gian ( t: tham số) Phương trình chính tắc : Giải : Ví dụ 4 : Chứng minh rằng đường thẳng d : vuông góc với mặt phẳng P ) Đường thẳng d có vtcp Mặt phẳng có vtpt Ta có: suy ra I/ Ph ươ ng trình tham số của đ ư ờng thẳng: A. x = 2 + 4t C. x = 4 + 2t y = - 3 – 6t y = - 6 – 3t z = 1 + 2t z = 2 + t B . x = 2 + 4t D. x = 4 + 2t y = -3 + 6t y = - 6 – 3t z = 1 + 2t z = 2 – 2t Tiết 35 - §3:Phương trình đường thẳng trong không gian Bài tập1 : Cho ®êng th¼ng ®i qua ®iÓm M(2;-3;1) vµ cã vÐc t¬ chØ ph¬ng =(4; - 6;2). Ph ươ ng trình tham số của đ ư ờng thẳng lµ: Bài tập củng cố Thì ph ươ ng trình tham số : ( t: tham số) Phương trình chính tắc : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Tiết 35 - §3:Phương trình đường thẳng trong không gian Thì ph ươ ng trình tham số : ( t: tham số) Phương trình chính tắc : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) Bài tập củng cố Bài tập2 : Cho đ ư ờng thẳng d c ú ph ươ ng trình tham số là : To ạ độ điểm M trên d và toạ độ một vectơ chỉ phương của d là: A. M(1; 2;0) vµ = (3; 1; 4) B. M(1;0;2) vµ = ( - 3; 0;4) C. M(1;2;0) vµ = ( - 3; 0; 4) D. M(-3; 0 ; 4) vµ = (1; 2; 0) I/ Ph ươ ng trình tham số của đ ư ờng thẳng: Thì ph ươ ng trình tham số : Đ ư ờng thẳng : - Đi qua M o (x o ;y o ;z o ) - Có véc t ơ chỉ ph ươ ng a = ( a 1 ;a 2 ;a 3 ) Tiết 35 - §3:Phương trình đường thẳng trong không gian ( t: tham số) Phương trình chính tắc : B ài tập 3 : Cho đường thẳng d có phương trình chính tắc : a)Hãy tìm một vec tơ chỉ phương và một điểm thuộc đường thẳng trên b) Hãy viết phương trình tham số của đường thẳng d. a) Đường thẳng d đi qua điểm M(1;0;3) và có vtcp Đáp số : b) Đường thẳng d có phương trình tham s ố là: Bài tập củng cố TRÂN TRỌNG KÍNH CHÀO VÀ CẢM ƠN! CHÚC CÁC EM HỌC TỐT - CỐ GẮNG LÊN !!! Hoan hô, bạn trả lời đúng rồi ! Rất tiếc , bạn đã sai rồi !
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_3_tiet_35_bai_3_phuong_trin.ppt
bai_giang_hinh_hoc_lop_12_chuong_3_tiet_35_bai_3_phuong_trin.ppt

