Bài giảng Hình học Lớp 12 - Chương 3: Phương pháp tọa độ trong không gian - Bài 3: Ứng dụng của tích phân trong hình học
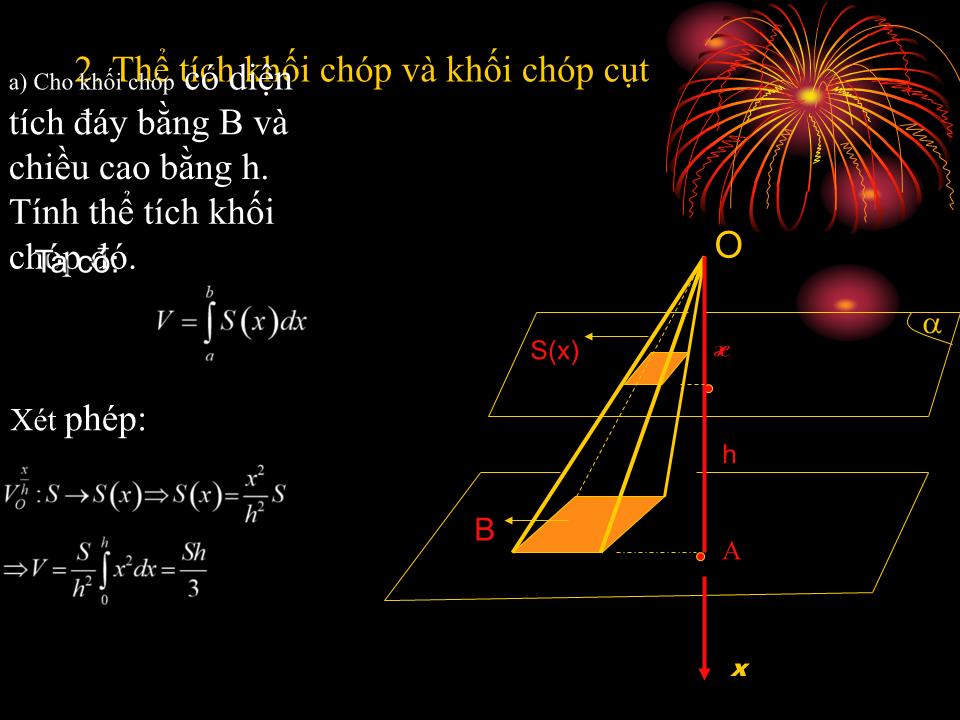
Thể tích khối chóp và khối chóp cụt
Cho khối chóp có diện tích đáy bằng B và chiều cao bằng h. Tính thể tích khối chóp đó.
Từ công thức và cách tính thể tích khối
chóp, hãy xác định công thức tính thể tích
khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B, B và chiều cao bằng h
Thể tích khối tròn xoay:
a). Giả sử hình giới hạn bởi các đường y = f(x), x = a, x = b, y = 0 quay quanh trục Ox
Tạo thành một vật thể tròn xoay T.
Thiết diện của vật thể T, với mp vuông góc với Ox tại điểm x, là một hình tròn bán kính y = f(x)
Diện tích thiết diện: S(x) = y2

Trang 1

Trang 2
Trang 3

Trang 4
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 12 - Chương 3: Phương pháp tọa độ trong không gian - Bài 3: Ứng dụng của tích phân trong hình học", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 3: Phương pháp tọa độ trong không gian - Bài 3: Ứng dụng của tích phân trong hình học

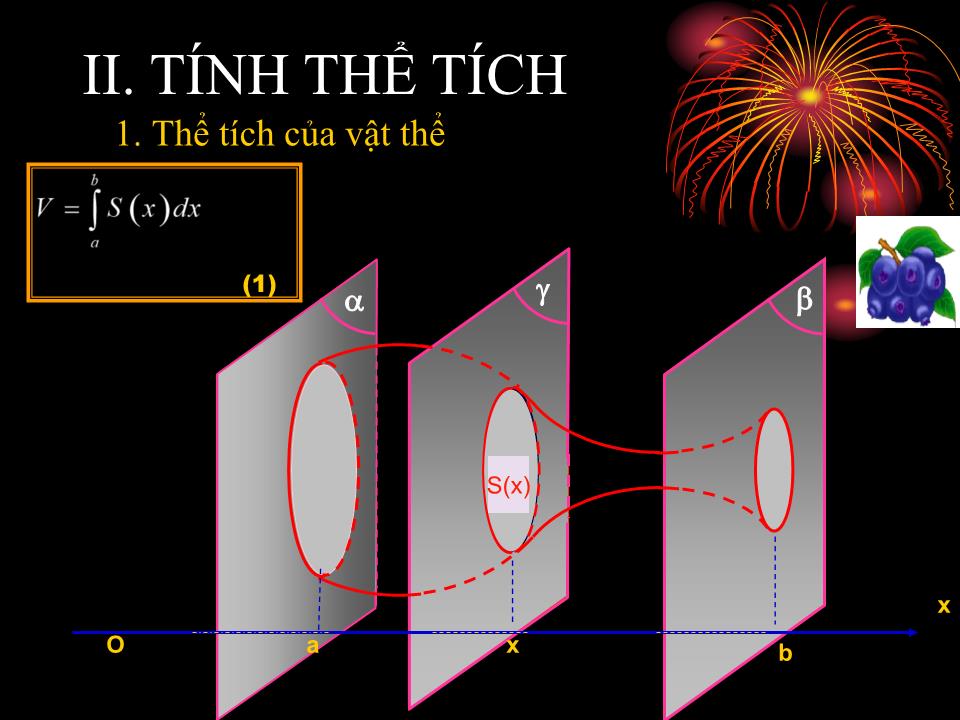
Bài 3: Ứng dụng của tích phân trong hình học Kiểm tra bài cũ: 1. Nêu các công thức tính diện tích hình phẳng ? Đáp án: - CT tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số f(x) liên tục, trục hoành và hai đường thẳng x=a, x=b là: - CT tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b] và các đường thẳng x=a, x=b là 2. Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h? 3. Hãy nhắc lại công thức tính thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h? V=Bh II. TÍNH THỂ TÍCH 1. Thể tích của vật thể S(x ) O a x b x S(x ) (1) Ví dụ 1 Tính thể tích khối lăng trụ , biết diện tích đáy bằng B và chiều cao bằng h. S(x )=B h x O x Giải : Chọn trục Ox song song với đường cao của khối lăng trụ , còn hai đáy nằm trong hai mặt phẳng vuông góc với Ox tại x=0 và x=h. Vậy một mặt phẳng tuỳ ý vuông góc với trục Ox, cắt lăng trụ theo thiết diện có diện tích không đổi S(x )=B; (0< x <h). Áp dụng CT (1) ta có : 2. Thể tích khối chóp và khối chóp cụt x O B S(x ) h x a) Cho khối chóp có diện tích đáy bằng B và chiều cao bằng h. Tính thể tích khối chóp đó . Ta có : Xét phép : A b) Từ công thức và cách tính thể tích khối chóp , hãy xác định công thức tính thể tích khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B, B và chiều cao bằng h Ta có : O B B x N M a b OM=a; ON=b (a<b); MN=h , S 3. Thể tích khối tròn xoay : a). Giả sử hình giới hạn bởi các đường y = f(x ), x = a, x = b, y = 0 quay quanh trục Ox Tạo thành một vật thể tròn xoay T. Thiết diện của vật thể T, với mp vuông góc với Ox tại điểm x, là một hình tròn bán kính y = f(x ) Diện tích thiết diện : S(x ) = y 2 Thể tích V của vật thể : Ví dụ2: Xét hình phẳng giới hạn bởi đồ thị hàm số các đường thẳng x=1, x=2 và trục hoành . Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng đó quanh trục hoành . 1 2 O x y Đáp số Bạn giỏi quá ! Ví dụ 3: Cho hình phẳng A giới hạn bởi các đường y= cosx , y=0, x=0 và x= Π /4. t ính th ể t ích c ủa kh ối tr òn xoay t ạo th ành khi quay h ình A quanh tr ục ho ành Đáp số Đúng rồi ! Ví dụ 4: Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0<x<3) là một hình chữ nhật có hai kích thước là x và Đáp số Bạn giỏi quá ! 11 XIN CẢM ƠN QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_3_phuong_phap_toa_do_trong.ppt
bai_giang_hinh_hoc_lop_12_chuong_3_phuong_phap_toa_do_trong.ppt

