Bài giảng Hình học Lớp 12 - Chương 3 - Bài 2: Phương trình mặt phẳng
1.Phương trình mặt
phẳng
a. Vectơ pháp tuyến
của mặt phẳng.
b.Phương trình tổng
quát của mặt phẳng.
2.Các trường hợp
riêng.
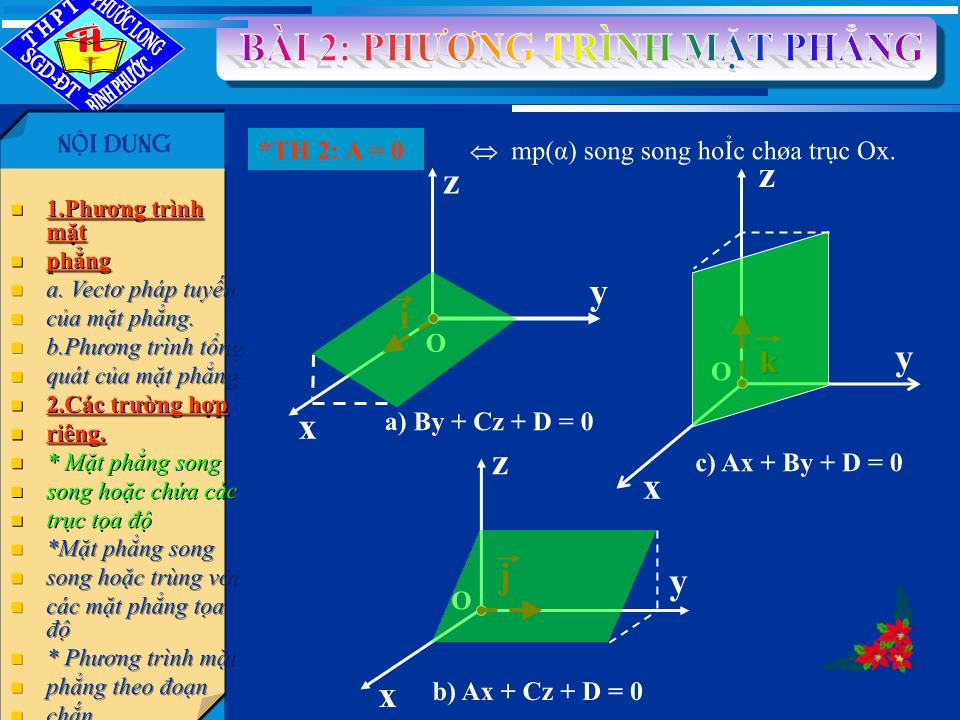
* Mặt phẳng song
song hoặc chứa các
trục tọa độ.
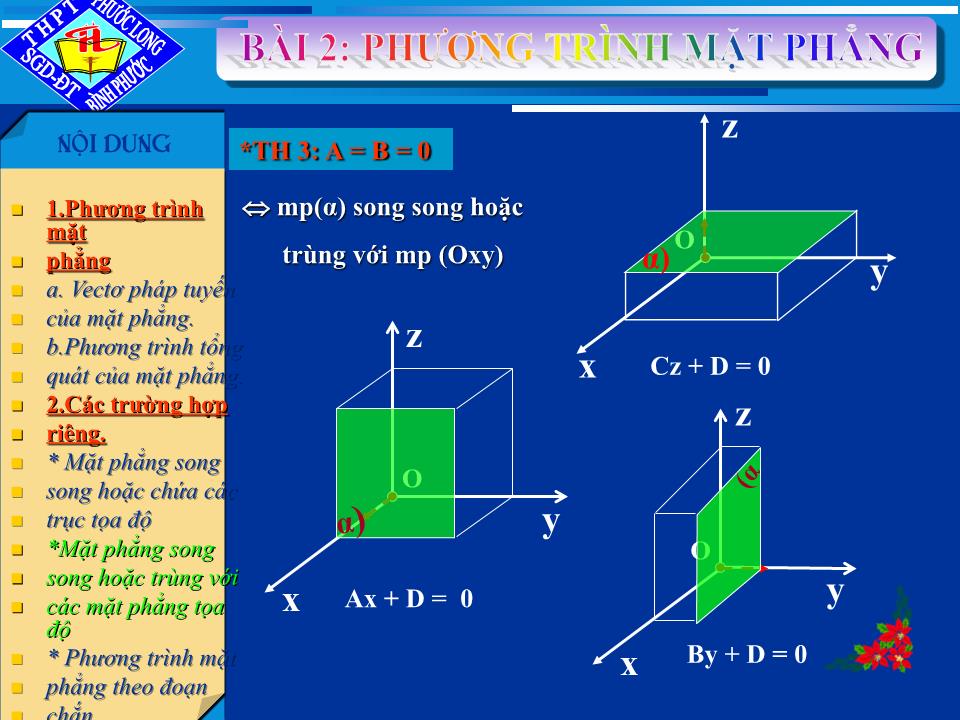
*Mặt phẳng song
song hoặc trùng với
các mặt phẳng tọa độ
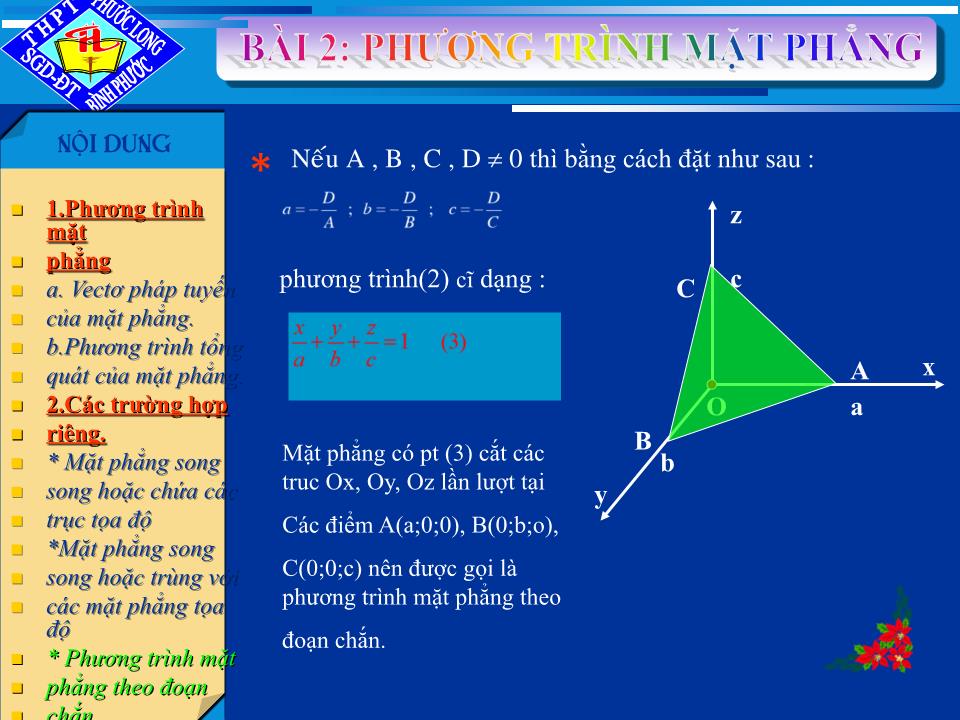
* Phương trình mặt
phẳng theo đoạn
chắn
a. Véc tơ pháp tuyến (vtpt) của mặt phẳng:
Định nghĩa: Vectơ được gọi là
vectơ pháp tuyến của mặt phẳng () nếu
giá của vuông góc với mp ().
Chú ý:
1.Nếu là vtpt của () thì
cũng là vtpt của ().
2. Nếu () // () thì vtpt
của mp này cũng là vtpt của mp kia.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 12 - Chương 3 - Bài 2: Phương trình mặt phẳng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 3 - Bài 2: Phương trình mặt phẳng

PHƯƠNG TRÌNH MẶT PHẲNG BÀI :2 GIÁO VIÊN : HUỲNH THỊ HỒNG ANH TRƯỜNG THPT LỘC HƯNG Tiết : 1-2 Cho điểm A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) a) Tính : b) Cho biết mối quan hệ giữa với mặt phẳng : (ABC) KIỂM TRA BÀI CŨ GIẢI : có giá vuông góc với mp(ABC) ) 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng . 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ. *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn 1. Ph ươ ng trình mặt phẳng a. Véc t ơ pháp tuyến (vtpt) của mặt phẳng: Định nghĩa: Vect ơ đ ư ợc gọi là vect ơ pháp tuyến của mặt phẳng ( ) nếu giá của vuông góc với mp ( ). *Chú ý: 1.Nếu là vtpt của ( ) thì cũng là vtpt của ( ). 2. Nếu ( ) // ( ) thì vtpt của mp này cũng là vtpt của mp kia. 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng . 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0 b. Phương trình của mặt phẳng. M 0 Trong không gian Oxyz cho mặt phẳng ( ) qua điểm M 0 (x 0 ; y 0 ; z 0 ) và có vectơ pháp tuyến là : Điều kiện cần và đủ để M(x; y; z) ( ) là : ? ? Nếu đặt: D = -(Ax 0 + By 0 + Cz 0 ) thì (1) trở thành: Ax + By + Cz + D = 0 (1) (2) Vì : nên A 2 + B 2 + C 2 > 0 (2) gọi là phương trình mặt phẳng ( ) M 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng . 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn *Ví dụ 1: Viết phương trình mặt phẳng (P) trong mỗi trường hợp sau: 1 ./ Là mặt phẳng trung trực của đoạn thẳng EF, biết E (1;3;-2), F (-3; -5; 6) 2./ Đi qua 3 điểm M(1;0;0), N(0; 2; 0) và K(0; 0; 3) Giải : E F I 1. Gọi I là trung điểm của đoạn thẳng EF thì: ( P) Có vectơ pháp tuyến là : Vậy pt (P) là : x +2 y - 2 z + 7 = 0 3. PTTQ của mp ( ) đi qua điểm và nhận : làm vtpt là : A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0 2 . Mặt phẳng (P) đi qua M(1;0;0) Và có 1 vectơ pháp tuyến là : P M N K Vậy phương trình của mặt phẳng (P) là : 6x + 3y + 2z – 6 = 0 Hãy chỉ ra một điểm khác M,N,K của (P) ? *Ví dụ 2 : Trong không gian Oxyz mỗi phương trình sau đây có phải là phương trình của một mặt phẳng nào đó không ? x + y – z + 2 = 0 (1) x – 2y + z = 0 (2) x – y + 1 =0 (3) y – 3 = 0 (4) 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng . 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn *Định lí Trong không gian Oxyz, mỗi ph ươ ng trình : Ax + By + Cz + D = 0 với đều là ph ươ ng trình của một mặt phẳng xác định. 2. Các tr ư ờng hợp riêng Trong không gian cho Oxyz cho mp ( α ) : Ax + By + Cz + D = 0 (2) *TH 1: D=0 x y z Phương trình (2) có dạng : Ax + By + Cz = 0 Mp ( α ) ®i qua gèc to¹ ®é x α O *TH 2: A = 0 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn mp( α ) song song hoỈc chøa trục Ox. z x y O i a) By + Cz + D = 0 x y z j b) Ax + Cz + D = 0 O z x y O k c) Ax + By + D = 0 k *TH 3: A = B = 0 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn mp( α ) song song hoặc trùng với mp (Oxy) z y O x Cz + D = 0 α ) z x y O Ax + D = 0 α ) y By + D = 0 x O z ( α 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn * Neáu A , B , C , D 0 thì bằng cách đặt như sau : p hương trình (2) cĩ dạng : Mặt phẳng có pt (3) cắt các truc Ox, Oy, Oz lần lượt tại Các điểm A(a;0;0), B(0;b;o), C(0;0;c) nên được gọi là phương trình mặt phẳng theo đoạn chắn. c C b B a A O x y z 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn 2. Các tr ư ờng hợp riêng : Dạng ph ươ ng trình Vị trí của mặt phẳng so với các yếu tố cúa hệ toạ độ Ax + By + Cz = 0 Đi qua gốc toạ độ O Ax + By + D = 0 Song song hoặc chứa trục Oz Ax + Cz + D = 0 Song song hoặc chứa trục Oy By + Cz + D = 0 Song song hoặc chứa trục Ox Ax + D = 0 Song song hoặc trùng với mặt phẳng (Oyz) By + D = 0 Song song hoặc trùng với mặt phẳng (Oxz) Cz + D = 0 Song song hoặc trùng với mặt phẳng (Oxy) 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn *Ví dụ 3 : Trong không gian Oxyz cho điểm M(30;15;6) Gọi A, B, C, lần lượt là hỡnh chiếu của M lờn cỏc trục Ox, Oy, Oz Hãy viết ph ươ ng trình mặt phẳng (P) đi qua các hình chiếu của M trên các trục toạ độ b. Viết phương trình mặt phẳng (Q) chứa A, B và song song với OM Giải *a. Toạ độ hình chiếu của M trên các trục toạ độ là : A(30;0;0), B(0;15;0), C(0;0;6) Ph ươ ng mặt phẳng (P) qua A, B, C là : 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn O M Q A B O’ M’ * b. Ta có 1 vtpt của (Q) là : Vậy phương trình của mặt (Q) là : x + 2y + 10z - 30 = 0 1.Phương trình mặt phẳng a. Vectơ pháp tuyến của mặt phẳng. b.Phương trình tổng quát của mặt phẳng. 2.Các trường hợp riêng. * Mặt phẳng song song hoặc chứa các trục tọa độ *Mặt phẳng song song hoặc trùng với các mặt phẳng tọa độ * Phương trình mặt phẳng theo đoạn chắn CỦNG CỐ KIẾN THỨC Điền vào dấu . . . 1. Để viết PTTQ của mp ( ) ta phải xác định: . . . * một VTPT của mp ( ) * một điểm mp ( ) đi qua 2. Hai vectơ không cùng phương a và b có giá song song hoặc nằm trong mp ( ) thì mp ( ) có một VTPT là: . . . 3. PTTQ của mp ( ) đi qua điểm và nhận làm vtpt là : . . . A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0 4. Nếu mp ( ) có PTTQ : Ax + By + Cz + D = 0 thì nó có một VTPT là: . . . n = (A;B;C) Ghi nhớ n =[ a , b] CHÚC CÁC EM LUÔN THÀNH CÔNG TRONG HỌC TẬP XIN CHÂN THÀNH CẢM ƠN !
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_3_bai_2_phuong_trinh_mat_ph.ppt
bai_giang_hinh_hoc_lop_12_chuong_3_bai_2_phuong_trinh_mat_ph.ppt

