Bài giảng Hình học Lớp 12 - Chương 3 - Bài 1: Hệ toạ độ trong không gian
Hệ toạ độ
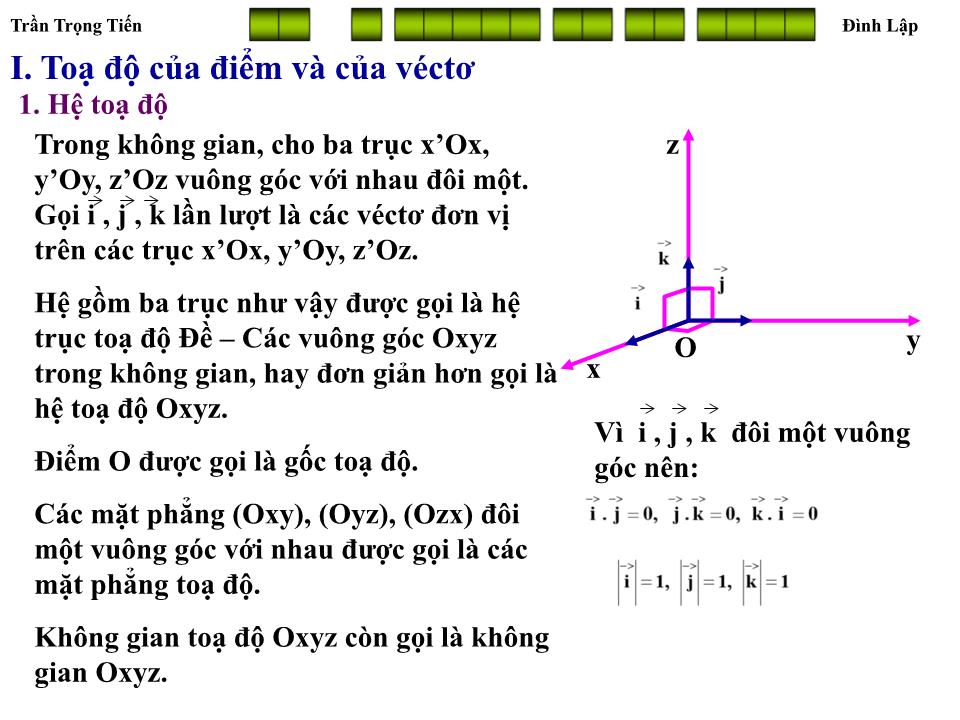
Trong không gian, cho ba trục x’Ox, y’Oy, z’Oz vuông góc với nhau đôi một. Gọi i , j , k lần lượt là các véctơ đơn vị trên các trục x’Ox, y’Oy, z’Oz.
Hệ gồm ba trục như vậy được gọi là hệ trục toạ độ Đề – Các vuông góc Oxyz trong không gian, hay đơn giản hơn gọi là hệ toạ độ Oxyz.
Điểm O được gọi là gốc toạ độ.
Các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau được gọi là các mặt phẳng toạ độ.
Không gian toạ độ Oxyz còn gọi là không gian Oxyz.
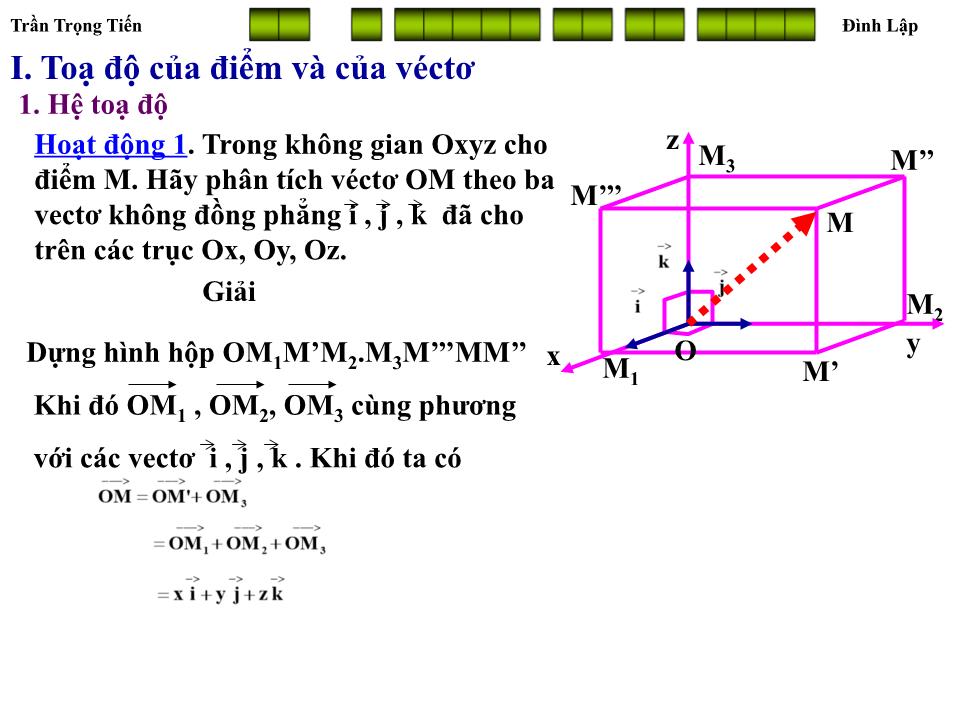
Hoạt động 1. Trong không gian Oxyz cho điểm M. Hãy phân tích véctơ OM theo ba vectơ không đồng phẳng i , j , k đã cho trên các trục Ox, Oy, Oz.

Trang 1
Trang 2
Trang 3
Trang 4
Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 12 - Chương 3 - Bài 1: Hệ toạ độ trong không gian", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 3 - Bài 1: Hệ toạ độ trong không gian

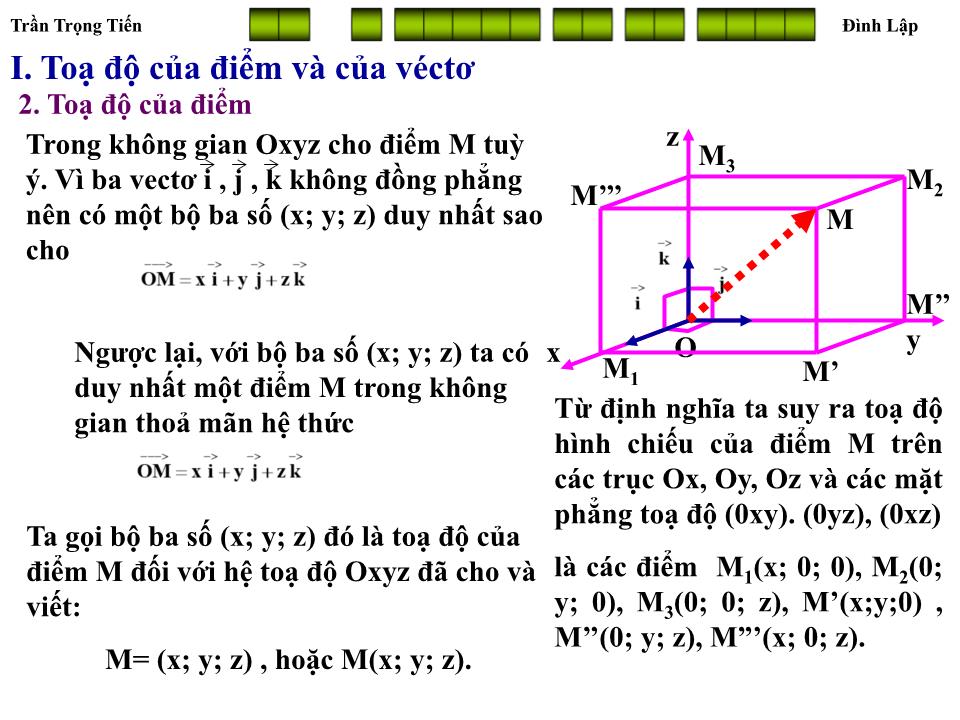
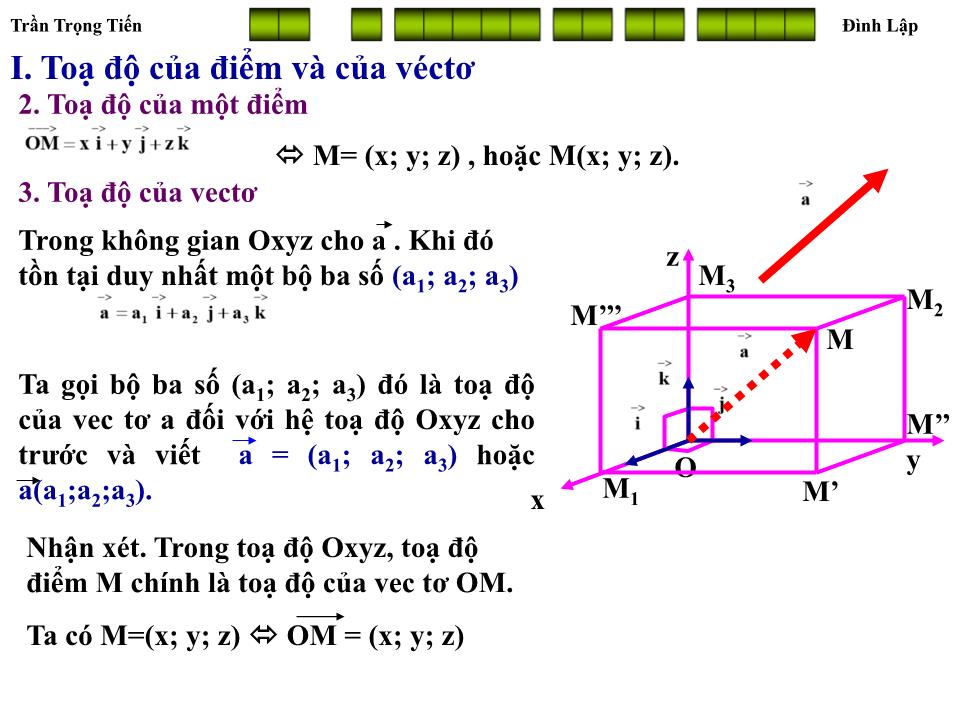
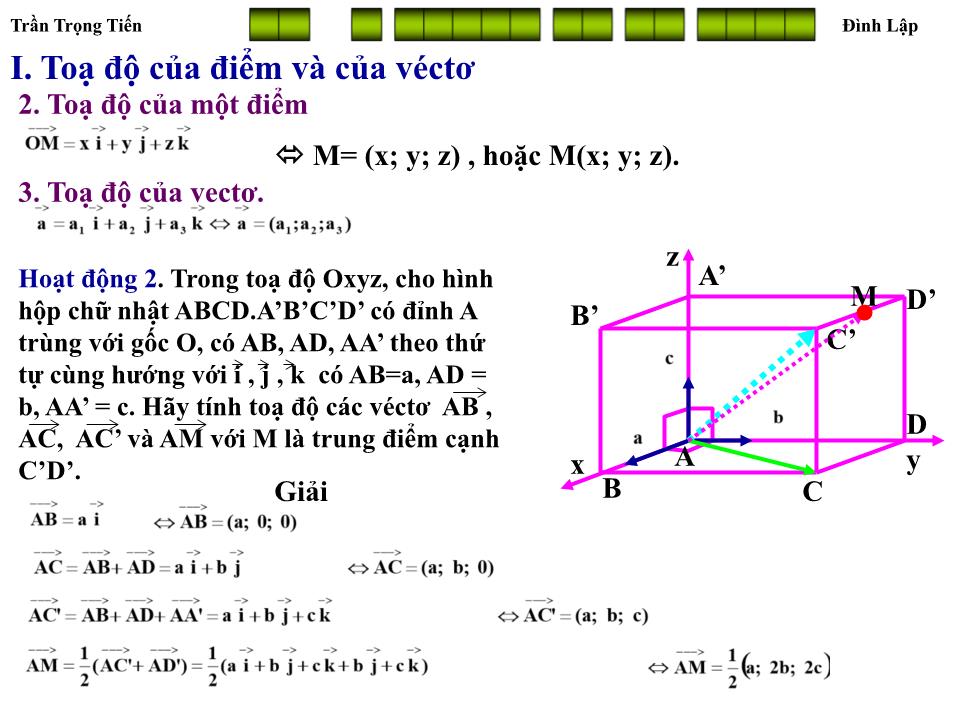
TRƯỜNG THPT ĐÌNH LẬP Đình Lập Lạng Sơn T H P T Đình Lập ĐL Giáo viên soạn: Trần Trọng Tiến HỆ TOẠ ĐỘ TRONG KHÔNG GIAN __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ 1. Hệ toạ độ Trong không gian, cho ba trục x’Ox, y’Oy, z’Oz vuông góc với nhau đôi một. Gọi i , j , k lần l ư ợt là các véct ơ đ ơ n vị trên các trục x’Ox, y’Oy, z’Oz. Hệ gồm ba trục nh ư vậy đ ư ợc gọi là hệ trục toạ độ Đề – Các vuông góc Oxyz trong không gian, hay đ ơ n giản h ơ n gọi là hệ toạ độ Oxyz. Điểm O đ ư ợc gọi là gốc toạ độ. Các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau đ ư ợc gọi là các mặt phẳng toạ độ. Không gian toạ độ Oxyz còn gọi là không gian Oxyz. O y x z Vì i , j , k đôi một vuông góc nên: Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ 1. Hệ toạ độ Hoạt động 1 . Trong không gian Oxyz cho điểm M. Hãy phân tích véct ơ OM theo ba vect ơ không đồng phẳng i , j , k đã cho trên các trục Ox, Oy, Oz. Giải Dựng hình hộp OM 1 M’M 2 .M 3 M’’’MM’’ Khi đó OM 1 , OM 2 , OM 3 cùng ph ươ ng với các vect ơ i , j , k . Khi đó ta có M’’ M’ M 1 M 3 M’’’ M 2 O y x z M Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ 2. Toạ độ của điểm O y x z M M 2 M’ M 1 M 3 M’’’ M’’ Trong không gian Oxyz cho điểm M tuỳ ý. Vì ba vect ơ i , j , k không đồng phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho Ng ư ợc lại, với bộ ba số (x; y; z) ta có duy nhất một điểm M trong không gian thoả mãn hệ thức Ta gọi bộ ba số (x; y; z) đó là toạ độ của điểm M đối với hệ toạ độ Oxyz đã cho và viết: M= (x; y; z) , hoặc M(x; y; z). Từ định nghĩa ta suy ra toạ độ hình chiếu của điểm M trên các trục Ox, Oy, Oz và các mặt phẳng toạ độ (0xy). (0yz), (0xz) là các điểm M 1 (x; 0; 0), M 2 (0; y; 0), M 3 (0; 0; z), M’(x;y;0) , M’’(0; y; z), M”’(x; 0; z). Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ 2. Toạ độ của một điểm M 2 M= (x; y; z) , hoặc M(x; y; z). O y x z M M’ M 1 M 3 M’’’ M’’ 3. Toạ độ của vect ơ Trong không gian Oxyz cho a . Khi đó tồn tại duy nhất một bộ ba số (a 1 ; a 2 ; a 3 ) Ta gọi bộ ba số (a 1 ; a 2 ; a 3 ) đó là toạ độ của vec t ơ a đối với hệ toạ độ Oxyz cho tr ư ớc và viết a = (a 1 ; a 2 ; a 3 ) hoặc a(a 1 ;a 2 ;a 3 ). Nhận xét. Trong toạ độ Oxyz, toạ độ điểm M chính là toạ độ của vec t ơ OM. Ta có M=(x; y; z) OM = (x; y; z) Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ 2. Toạ độ của một điểm M= (x; y; z) , hoặc M(x; y; z). 3. Toạ độ của vect ơ . Hoạt động 2 . Trong toạ độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có AB, AD, AA’ theo thứ tự cùng h ư ớng với i , j , k có AB=a, AD = b, AA’ = c. Hãy tính toạ độ các véct ơ AB , AC, AC’ và AM với M là trung điểm cạnh C’D’. Giải A y x z C’ D’ C B A’ B’ D M Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ M= (x; y; z) II. BTTĐ của các phép toán vect ơ . Trong không gian Oxyz cho hai vect ơ Chứng minh Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ M= (x; y; z) II. BTTĐ của các phép toán vect ơ . Trong không gian Oxyz cho hai vect ơ c) a và b cùng ph ươ ng khi và chỉ khi a 1 =kb 1 , a 2 = kb 2 , a 3 = ka 3 e) M là trung điểm AB khi và chỉ khi Ví dụ 1. Cho A(1; 3; 2), B(3;-2;1) và C(4;-1;3). Tìm toạ độ điểm D sao cho ABCD là hình bình hành. Giải Do ABCD là hình bình hành khi đó ta có: A B C D Vậy D = (2; 4; 4) Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ M= (x; y; z) II. BTTĐ của các phép toán vect ơ . Trong không gian Oxyz cho hai vect ơ c) a và b cùng ph ươ ng khi và chỉ khi a 1 =kb 1 , a 2 = kb 2 , a 3 = ka 3 e) M là trung điểm AB khi và chỉ khi Ví dụ 2. Cho A(1; 1; 1), B(0;7/3;2/3) và C(7/4; 0; 5/4). Chứng minh A, B, C thẳng hàng. Giải => AB , AC cùng ph ươ ng hay A, B, C thẳng hàng. Trần Trọng Tiến Đình Lập __ _ _____ __ __ ____ I. Toạ độ của điểm và của véct ơ M= (x; y; z) II. BTTĐ của các phép toán vect ơ . Trong không gian Oxyz cho hai vect ơ c) a và b cùng ph ươ ng khi và chỉ khi a 1 =kb 1 , a 2 = kb 2 , a 3 = ka 3 e) M là trung điểm AB khi và chỉ khi Ví dụ 3. Cho A(1; 3; 2), M(3;-2;1) . Tìm toạ độ điểm B sao cho A, B đối xứng nhau qua điểm M. Giải Do A và B đối xứng nhau qua M nên M là trung điểm AB, nên ta có Vậy toạ độ điểm B = (5; -7; 0) Trần Trọng Tiến Đình Lập CỦNG CỐ Qua bài học học sinh cần nắm đ ư ợc Hệ toạ độ trong không gian. Toạ độ của vect ơ . Toạ độ của điểm, toạ độ hình chiếu của một điểm trên các trục toạ độ và các mặt phẳng toạ độ. Các phép toán về vect ơ . Điều kiện ba điểm thẳng hàng, ph ươ ng pháp tìm toạ độ của một điểm qua phép đối xứng tâm.
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_3_bai_1_he_toa_do_trong_kho.ppt
bai_giang_hinh_hoc_lop_12_chuong_3_bai_1_he_toa_do_trong_kho.ppt

