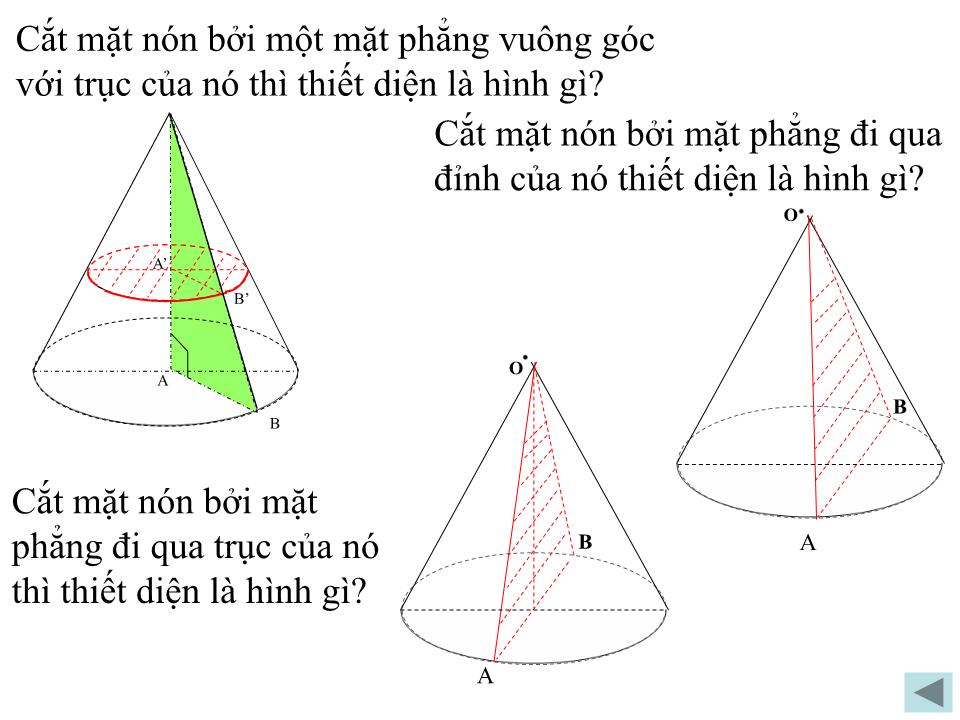
Bài giảng Hình học Lớp 12 - Chương 2: Mặt nón, mặt trụ, mặt cầu - Tiết 12: Khái niệm về mặt tròn xoay - Đào Thị Hương Hoa
SỰ TẠO THÀNH MẶT TRÒN XOAY
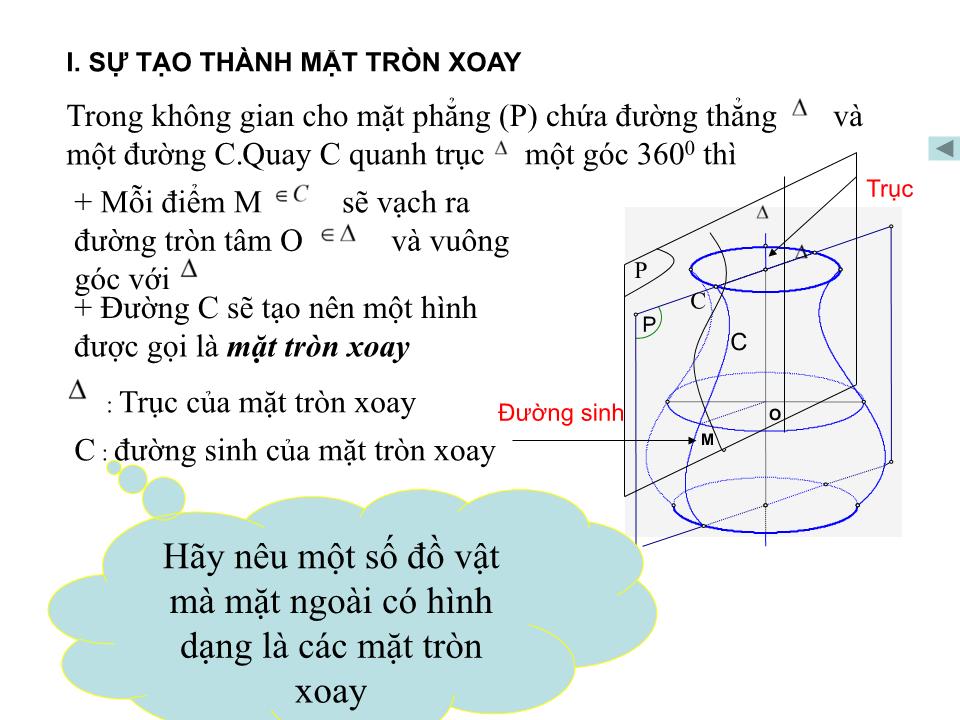
Trong không gian cho mặt phẳng (P) chứa đường thẳng và một đường C.
Quay C quanh trục một góc 3600 thì
+ Mỗi điểm M sẽ vạch ra đường tròn tâm O và vuông góc với
+ Đường C sẽ tạo nên một hình được gọi là mặt tròn xoay
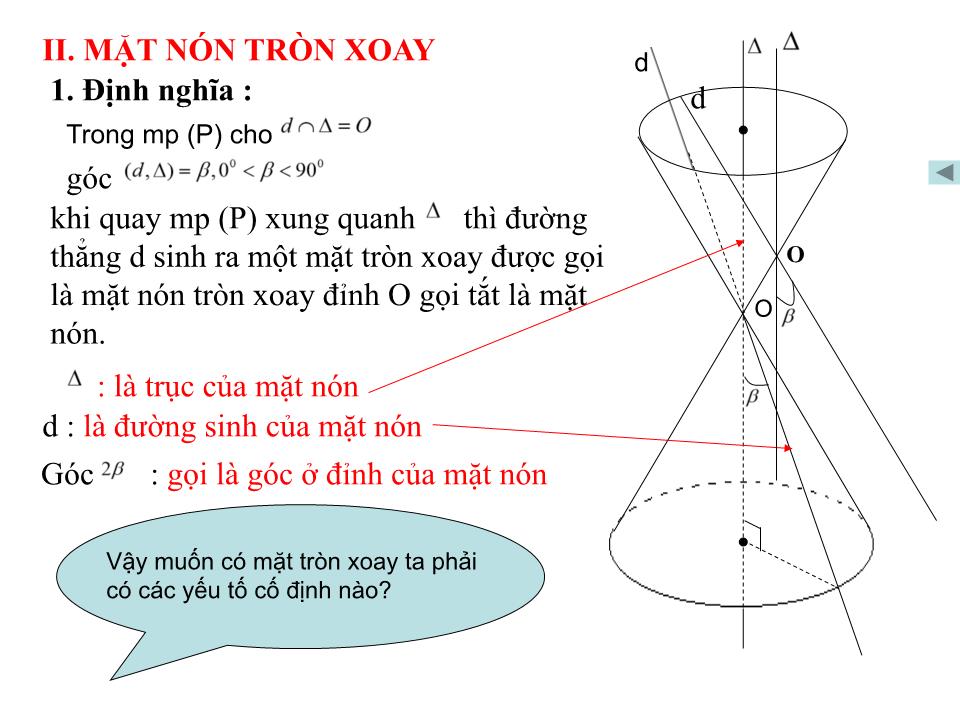
Trong mp (P) cho
góc
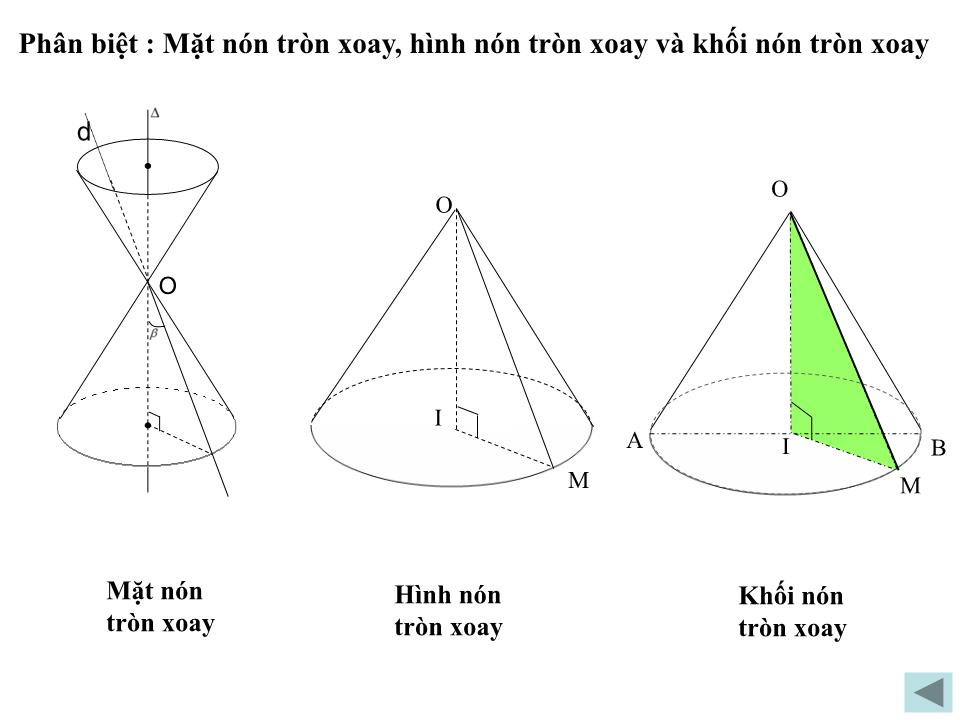
khi quay mp (P) xung quanh thì đường thẳng d sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh O gọi tắt là mặt nón.
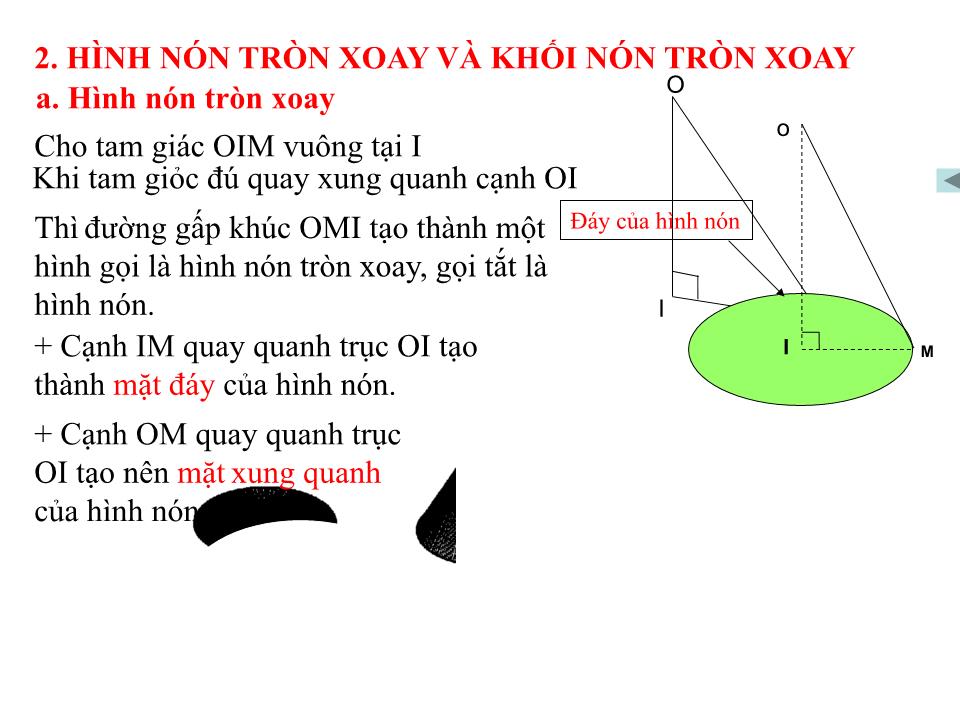
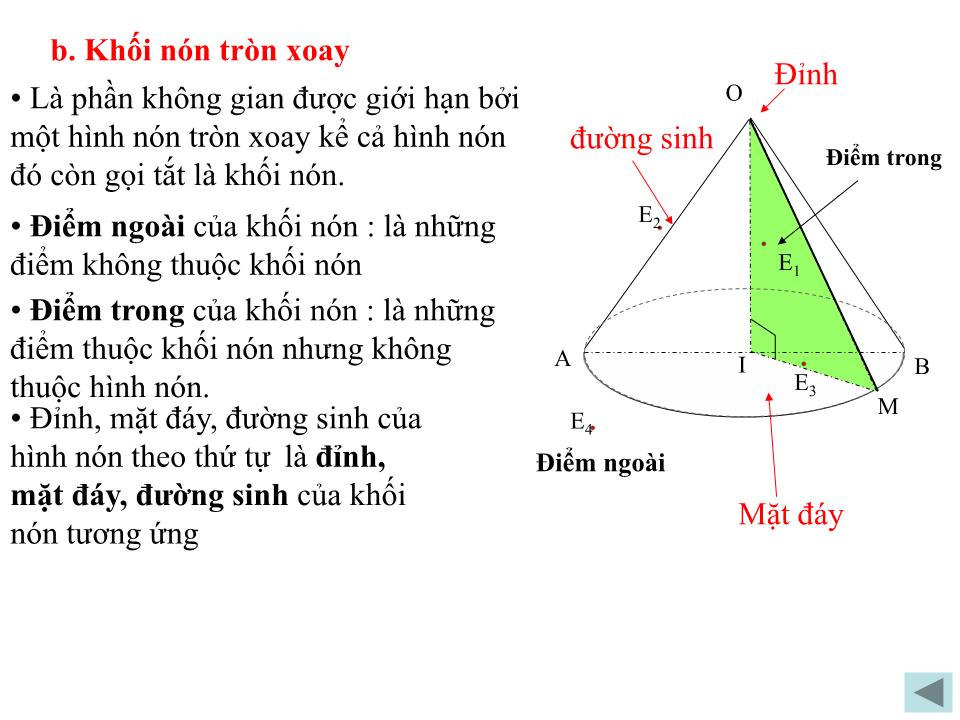
Cho tam giác OIM vuông tại I
Khi tam giỏc đú quay xung quanh cạnh OI
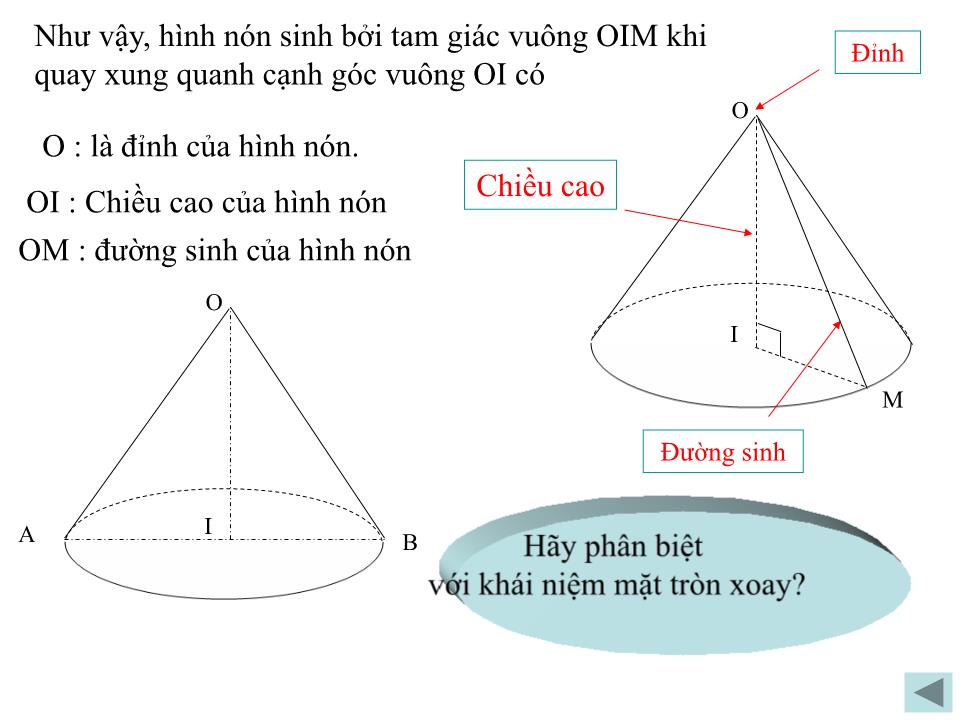
Thì đường gấp khúc OMI tạo thành một hình gọi là hình nón tròn xoay, gọi tắt là hình nón.
+ Cạnh IM quay quanh trục OI tạo thành mặt đáy của hình nón.
+ Cạnh OM quay quanh trục OI tạo nên mặt xung quanh của hình nón

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 2: Mặt nón, mặt trụ, mặt cầu - Tiết 12: Khái niệm về mặt tròn xoay - Đào Thị Hương Hoa

NHIỆT LIỆT CHÀO MỪNG CÁC THẦY, CÔ GIÁO VỀ DỰ GIỜ CHƯƠNG II : MẶT NÓN, MẶT TRỤ, MẶT CẦU TIẾT 12 : KHÁI NIỆM VỀ MẶT TRÒN XOAY GV : Đào Thị Hương Hoa Trường : THPT Thái Thuận. CH ƯƠ NG II : MẶT NÓN, MẶT TRỤ, MẶT CẦU TIẾT 12: KHÁI NIỆM VỀ MẶT TRÒN XOAY Bình hoa Chi tiết máy Chiếc nón I. SỰ TẠO THÀNH MẶT TRÒN XOAY Ca me ra Trong không gian cho mặt phẳng (P) chứa đường thẳng và một đường C. P C M O + Mỗi điểm M sẽ vạch ra đường tròn tâm O và vuông góc với + Đường C sẽ tạo nên một hình được gọi là mặt tròn xoay I. SỰ TẠO THÀNH MẶT TRÒN XOAY Đường sinh Trục Hãy nêu một số đồ vật mà mặt ngoài có hình dạng là các mặt tròn xoay P C : Trục của mặt tròn xoay C : đường sinh của mặt tròn xoay Quay C quanh trục một góc 360 0 thì II. MẶT NÓN TRÒN XOAY 1. Định nghĩa : O d Trong mp (P) cho d : là đường sinh của mặt nón : là trục của mặt nón Góc : gọi là góc ở đỉnh của mặt nón khi quay mp (P) xung quanh thì đường thẳng d sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh O gọi tắt là mặt nón. góc Vậy muốn có mặt tròn xoay ta phải có các yếu tố cố định nào? d O o M I Mặt xung quanh của hình nón 2. HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY a. Hình nón tròn xoay Cho tam giác OIM vuông tại I Khi tam giỏc đú quay xung quanh cạnh OI + Cạnh IM quay quanh trục OI tạo thành mặt đáy của hình nón. Thì đường gấp khúc OMI tạo thành một hình gọi là hình nón tròn xoay, gọi tắt là hình nón. + Cạnh OM quay quanh trục OI tạo nên mặt xung quanh của hình nón O I M I M o Đáy của hình nón O I M Chiều cao Đỉnh Đường sinh O I A B O : là đỉnh của hình nón. OI : Chiều cao của hình nón OM : đường sinh của hình nón Như vậy, hình nón sinh bởi tam giác vuông OIM khi quay xung quanh cạnh góc vuông OI có Hãy phân biệt với khái niệm mặt tròn xoay? Cắt mặt nón bởi một mặt phẳng vuông góc với trục của nó thì thiết diện là hình gì? Cắt mặt nón bởi mặt phẳng đi qua đỉnh của nó thiết diện là hình gì? Cắt mặt nón bởi mặt phẳng đi qua trục của nó thì thiết diện là hình gì? A B B’ A’ A B O A B O b. Khối nón tròn xoay Là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó còn gọi tắt là khối nón. Điểm ngoài của khối nón : là những điểm không thuộc khối nón Điểm trong của khối nón : là những điểm thuộc khối nón nhưng không thuộc hình nón. M B O I A E 1 E 3 E 4 E 2 Điểm trong Điểm ngoài Đỉnh, mặt đáy, đường sinh của hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng Đỉnh Mặt đáy đường sinh O d M B O I A Phân biệt : Mặt nón tròn xoay, hình nón tròn xoay và khối nón tròn xoay Khối nón tròn xoay Hình nón tròn xoay Mặt nón tròn xoay O I M R : là bán kính đường tròn đáy : là độ dài đường sinh O I M 3. Diện tích xung quanh của hình nón tròn xoay R S tp = S xq + S đáy = a. Hình chóp nội tiếp hình nón b. Công thức tính diện tích xung quanh của hình nón . S O A 1 A 4 A 5 A 3 A 2 A 6 O I M Lg : S tp = S xq + S đáy = a Ví dụ 1 : Trong không gian cho tam giác OIM vuông tại I, góc và cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình nón tròn xoay. Tính Sxq, Stp của hình nón tròn xoay đó. 30 0 Ta có : OM = 2a S xq = b. Thể tích khối nón tròn xoay h : là chiều cao của khối nón R : là bán kính đường tròn đáy O I M R h O I M a 30 0 h Ví dụ 1 : Tính thể tích khối nón ? Lg : Ta có : Vậy khối nón tròn xoay có thể tích là : CỦNG CỐ Nắm được sự tạo thành mặt tròn xoay, mặt nón tròn xoay, hình nón tròn xoay, khối nón tròn xoay. Nắm được các yếu tố có liên quan : đỉnh, trục, đường sinh, mặt đáy, mặt xung quanh. Phân biệt được các khái niệm : mặt nón tròn xoay, hình nón tròn xoay, khối nón tròn xoay. Biết tính diện tích xung quanh của hình nón tròn xoay và thể tích của khối nón tròn xoay. Ví dụ 2 Cắt một mặt nón bởi một mặt phẳng đi qua trục của nó ta đ ư ợc thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh của hình nón đó và thể tích của khối nón t ươ ng ứng O C B A O d ’ Cho một đường thẳng d’,điều kiện để d’ thuộc mặt nón là gì ? Ta phải cm d’cắt đường thẳng cố định tại một điểm cố định , và tạo với đường cố định một góc không đổi , khi đó d’ là đường sinh của mặt nón VD1 Cho hai điểm A,B cố định và AB=20 một đ ư ờng thẳng d di động luôn đi qua A và cách B một khoảng h=10.C/m d luôn nằm trên mặt nón tròn xoay BG: Gọi là góc giữa AB và d Vậy d đi qua A tạo với AB một góc không đổi nên d nằm trên mặt nón đỉnh A,nhận AB làm trục,góc ở đỉnh 60 0 Ta phải cm d cắt đường thẳng cố định tại một điểm cố định , và tạo với đường cố định một góc không đổi , khi đó d là đường sinh của mặt nón A B H d 10 20 Khi đó ta có, trong tam giác vuông AHB
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_2_mat_non_mat_tru_mat_cau_t.ppt
bai_giang_hinh_hoc_lop_12_chuong_2_mat_non_mat_tru_mat_cau_t.ppt

