Bài giảng Hình học Lớp 12 - Chương 1 - Bài 1: Khái niệm về khối đa diện (Tiếp theo) - Phan Đình Lộc
Phép dời hình trong không gian
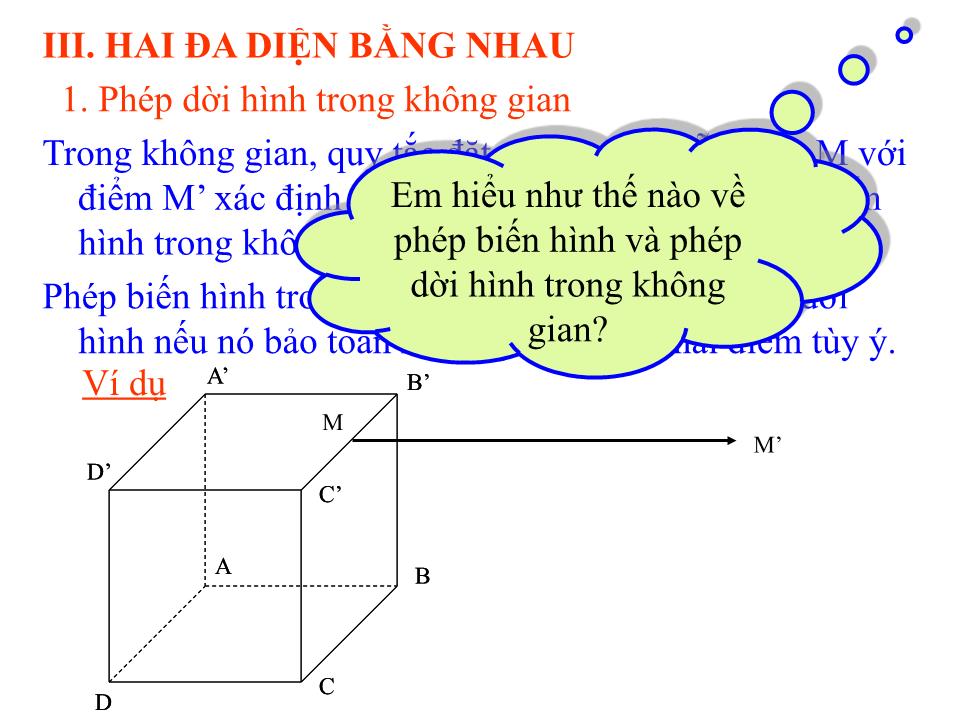
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với
điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian.
Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
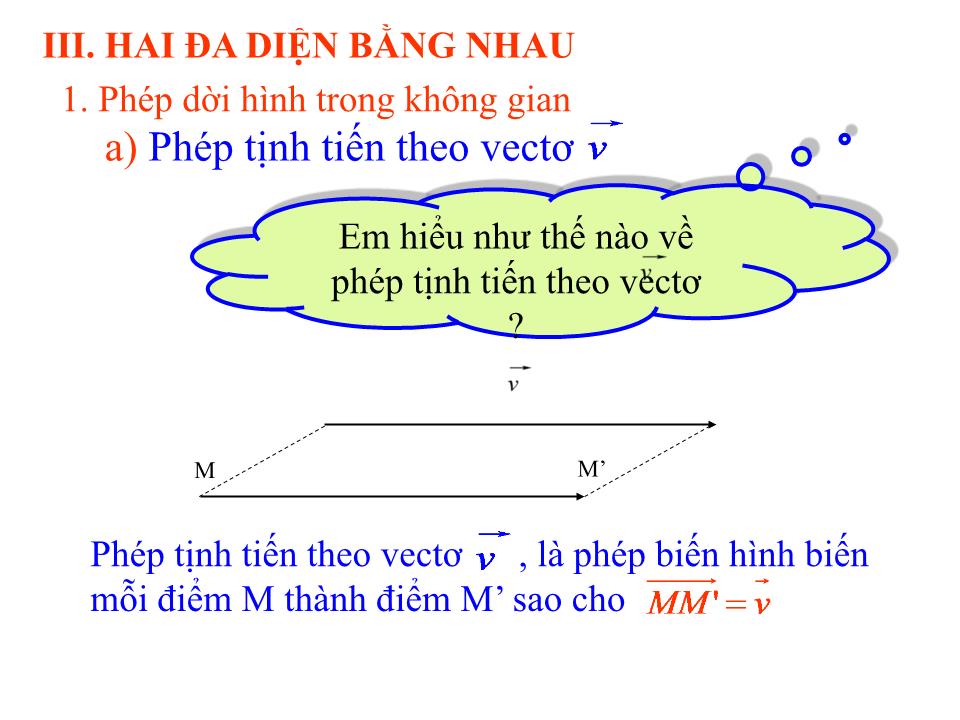
Phép tịnh tiến theo vectơ
Phép tịnh tiến theo vectơ , là phép biến hình biến mỗi điểm M thành điểm M’ sao cho
Phép dời hình trong không gian
a) Phép tịnh tiến theo vectơ
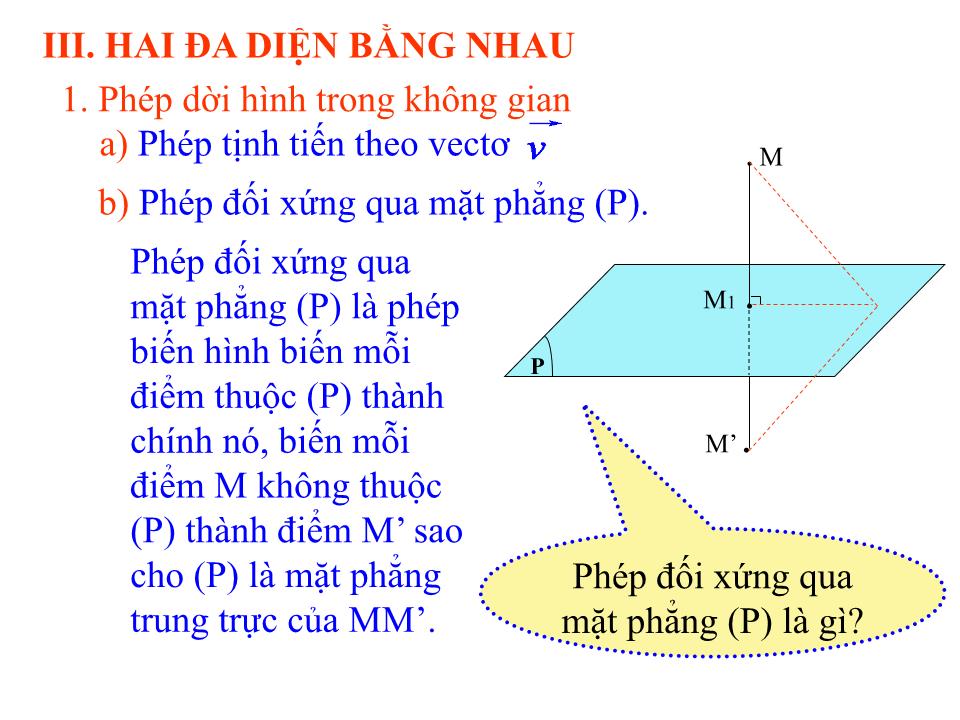
b) Phép đối xứng qua mặt phẳng (P).
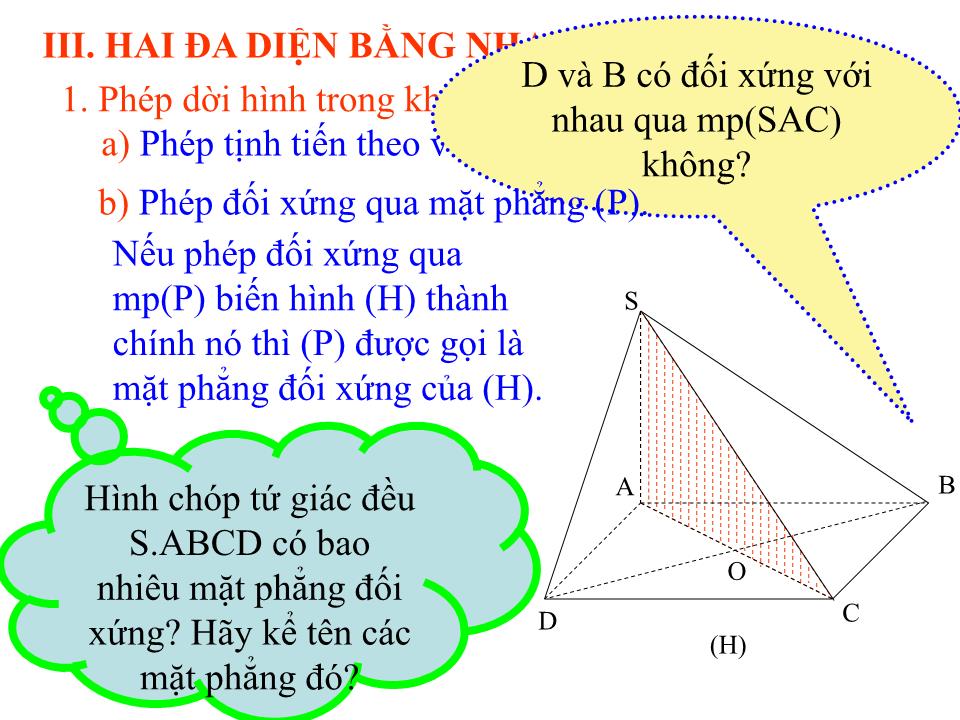
Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 12 - Chương 1 - Bài 1: Khái niệm về khối đa diện (Tiếp theo) - Phan Đình Lộc

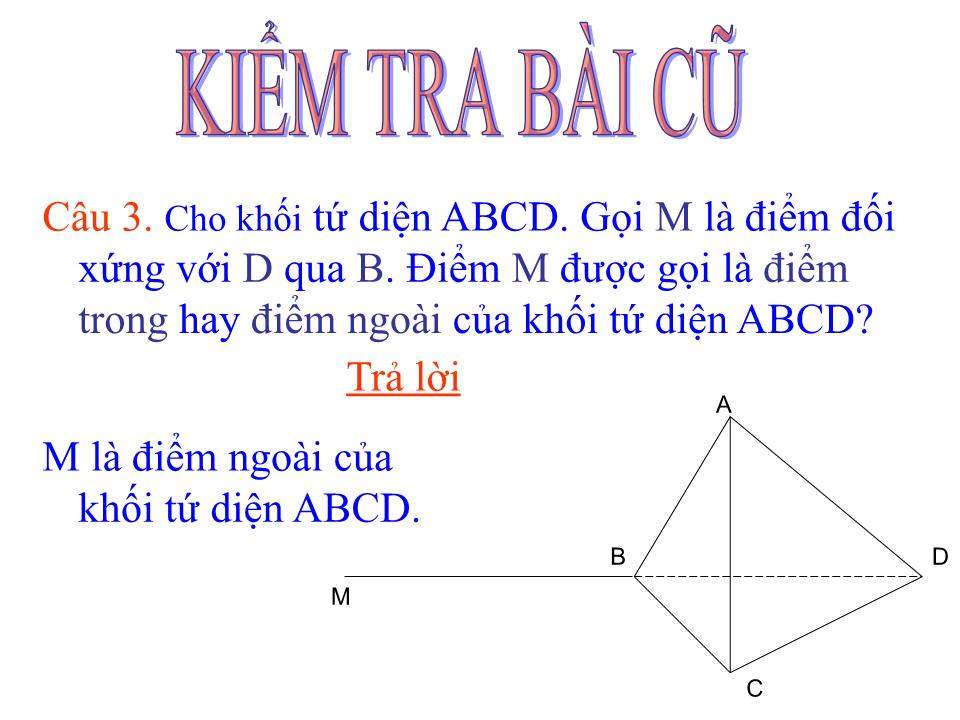
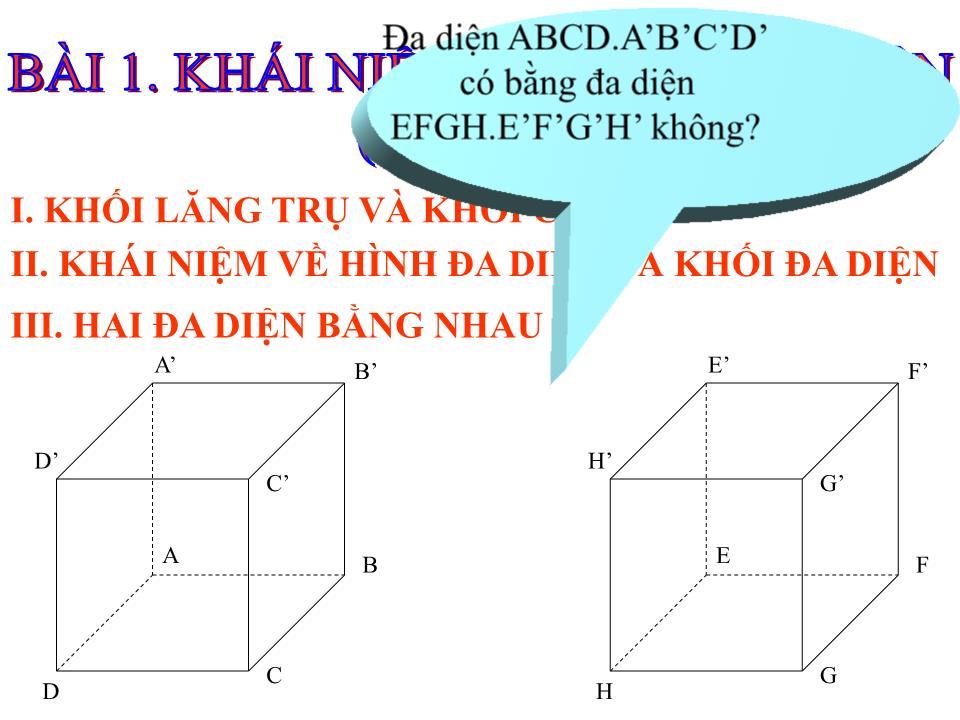
GIÁO VIÊN: PHAN ĐÌNH LỘC TỔ: TOÁN-LÝ-TIN MÔN: HÌNH HỌC LỚP: 12 Bài giảng: KHÁI NIỆM VỀ KHỐI ĐA DIỆN (tiếp) Tiết PPCT: 2 TRƯỜNG THPT ĐĂK GLONG Câu 1. Em hãy nêu khái niệm về hình đa diện? KIỂM TRA BÀI CŨ Trả lời Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau: b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung. Câu 2. Em hãy nêu khái niệm về khối đa diện? KIỂM TRA BÀI CŨ Trả lời Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó. KIỂM TRA BÀI CŨ Trả lời M là điểm ngoài của khối tứ diện ABCD. Câu 3. Cho khối tứ diện ABCD. Gọi M là điểm đối xứng với D qua B . Điểm M được gọi là điểm trong hay điểm ngoài của khối tứ diện ABCD? A B C D M I. KHỐI LĂNG TRỤ VÀ KHỐI CHÓP II. KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN BÀI 1. KHÁI NIỆM VỀ KHỐI ĐA DIỆN (Tiếp theo) III. HAI ĐA DIỆN BẰNG NHAU A B C D A’ B’ C’ D’ E F G H E’ F’ G’ H’ Đa diện ABCD.A’B’C’D’ có bằng đa diện EFGH.E’F’G’H’ không? III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian. Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý. Ví dụ A B C D A’ B’ C’ D’ Em hiểu như thế nào về phép biến hình và phép dời hình trong không gian? A B C D A’ B’ C’ D’ M M’ III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian Em hiểu như thế nào về phép tịnh tiến theo vectơ ? Phép tịnh tiến theo vectơ , là phép biến hình biến mỗi điểm M thành điểm M’ sao cho M M’ a) Phép tịnh tiến theo vectơ III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian a) Phép tịnh tiến theo vectơ P . M M 1 . M’ . Phép đối xứng qua mặt phẳng (P) là gì? Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’. b) Phép đối xứng qua mặt phẳng (P). III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian a) Phép tịnh tiến theo vectơ D và B có đối xứng với nhau qua mp(SAC) không? b) Phép đối xứng qua mặt phẳng (P). S D C B A O (H) Nếu phép đối xứng qua mp(P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H). Hình chóp tứ giác đều S.ABCD có bao nhiêu mặt phẳng đối xứng? Hãy kể tên các mặt phẳng đó? III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian a) Phép tịnh tiến theo vectơ b) Phép đối xứng qua mặt phẳng (P). c) Phép đối xứng tâm O. - Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó, biến điểm M khác O thành điểm M’ sao cho O là trung điểm của MM’. - Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H). . . . M O M’ A B C D O III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian a) Phép tịnh tiến theo vectơ b) Phép đối xứng qua mặt phẳng (P). A B C D O c) Phép đối xứng tâm O. - Phép đối xứng qua đường thẳng d là phép biến hình biến mỗi điểm thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của MM’. d d) Phép đối xứng qua đường thẳng d. III. HAI ĐA DIỆN BẰNG NHAU 1. Phép dời hình trong không gian a) Phép tịnh tiến theo vectơ b) Phép đối xứng qua mặt phẳng (P). A B C D O c) Phép đối xứng tâm O. - Nếu phép đối xứng qua đường thẳng d biến hình (H) thành chính nó thì d được gọi là trục đối xứng của (H). d d) Phép đối xứng qua đường thẳng d. Hình vuông ABCD có bao nhiêu trục đối xứng?
File đính kèm:
 bai_giang_hinh_hoc_lop_12_chuong_1_bai_1_khai_niem_ve_khoi_d.ppt
bai_giang_hinh_hoc_lop_12_chuong_1_bai_1_khai_niem_ve_khoi_d.ppt

