Bài giảng Hình học Lớp 11 - Tiết 34: Đường thẳng vuông góc với mặt phẳng (Tiếp theo) - Bùi Văn Long
Nội dung bài học
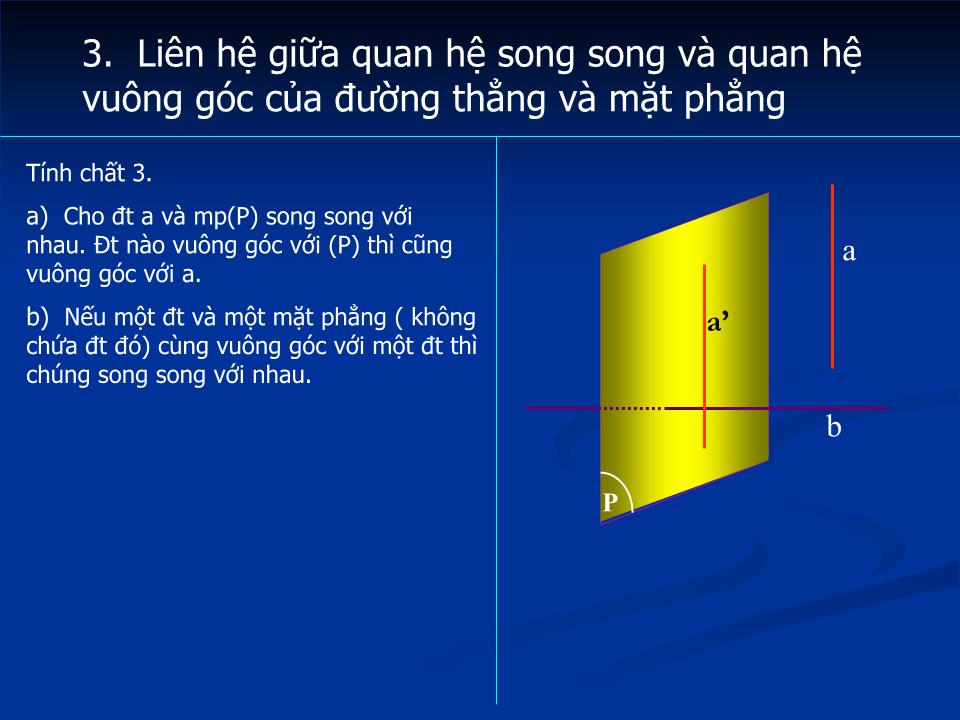
Liên hệ giữa quan hệ song song và quan hệ
vuông góc của đường thẳng và mặt phẳng
Định nghĩa và các tính chất của phép chiếu vuông góc.
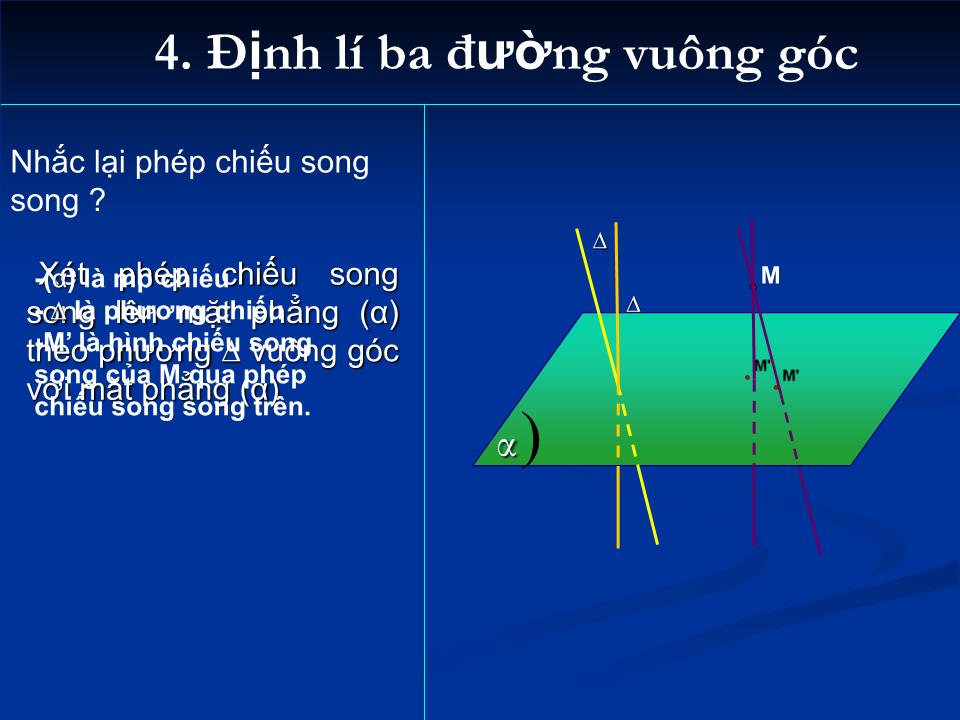
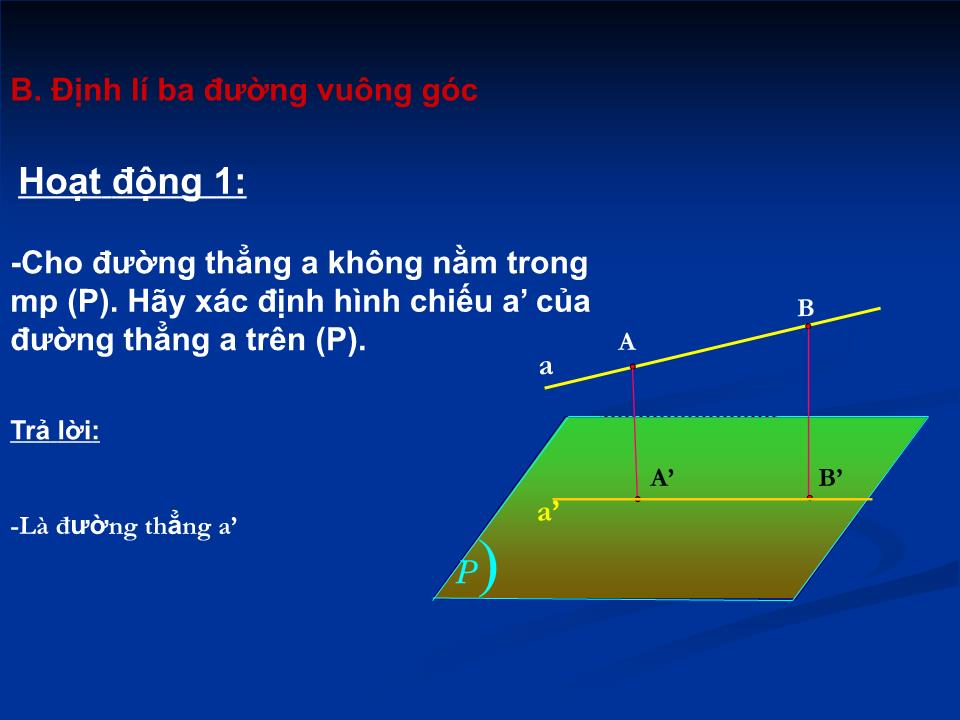
Định lí ba đường vuông góc
Góc giữa đường thẳng và mặt phẳng.
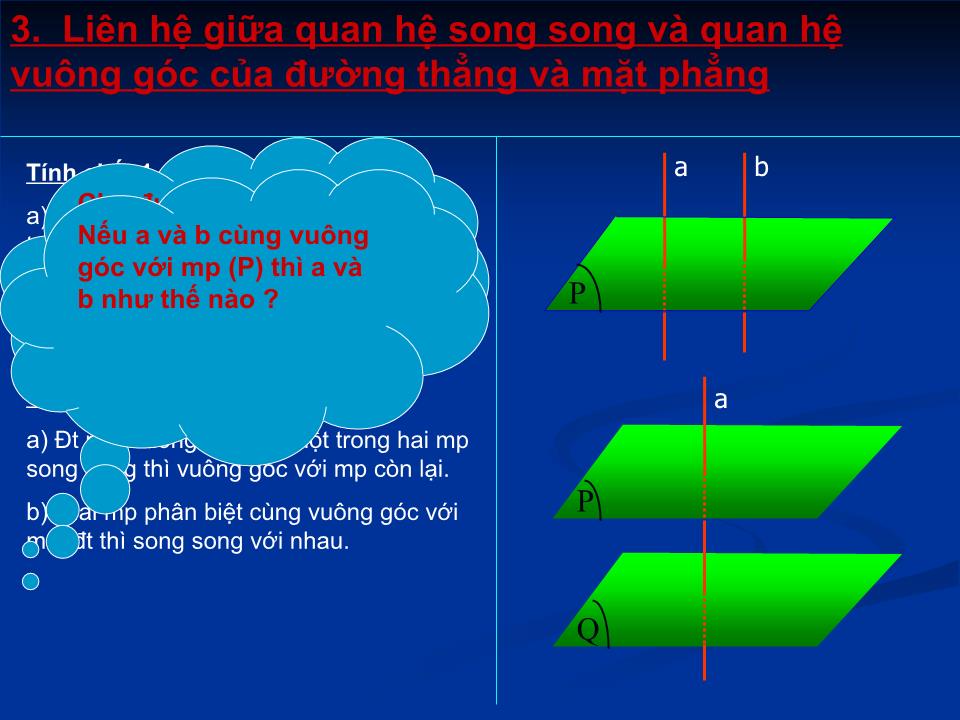
Tính chất 1.
Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Hai đt phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 2.
Đt nào vuông góc với một trong hai mp song song thì vuông góc với mp còn lại.
Hai mp phân biệt cùng vuông góc với một đt thì song song với nhau.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6

Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 11 - Tiết 34: Đường thẳng vuông góc với mặt phẳng (Tiếp theo) - Bùi Văn Long", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 11 - Tiết 34: Đường thẳng vuông góc với mặt phẳng (Tiếp theo) - Bùi Văn Long

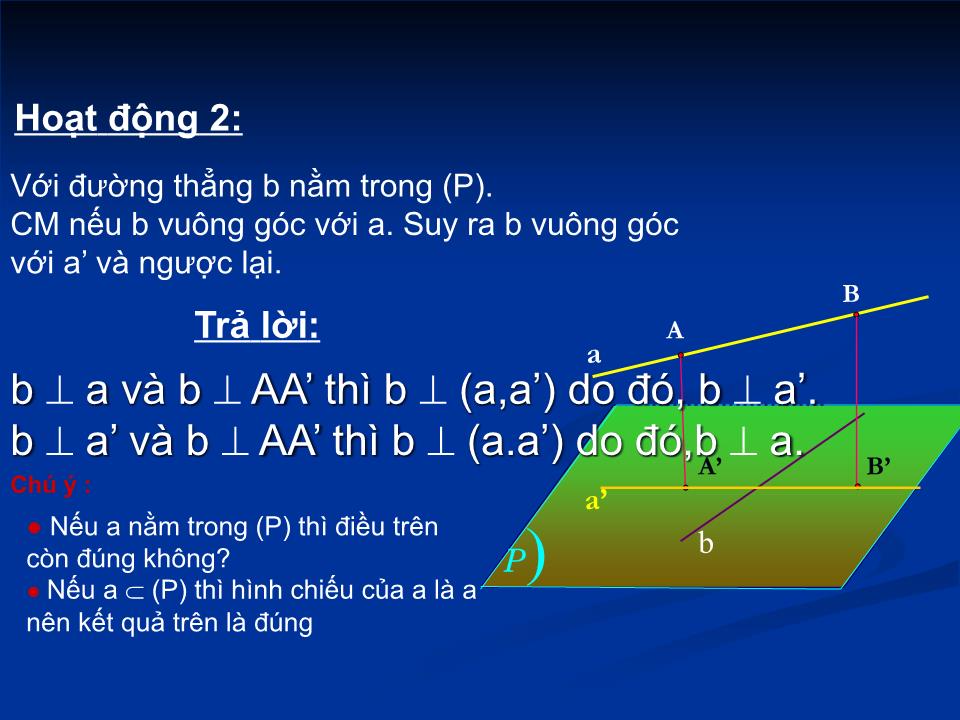
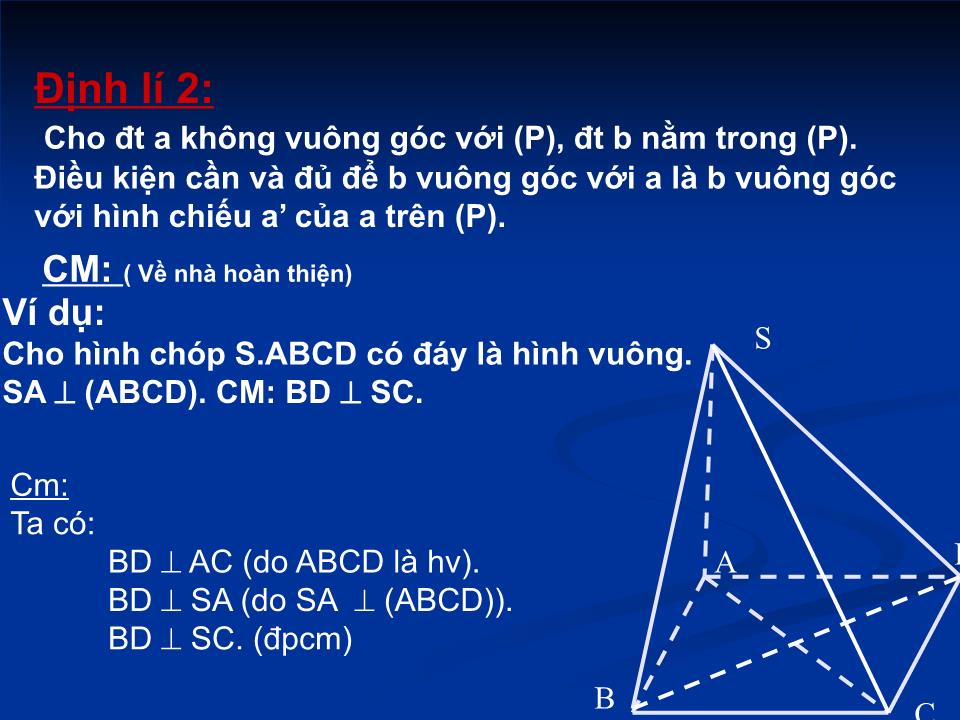
Chào mừng quý thầy cô giáo đến dự giờ! MÔN: TOÁN – LỚP 11B1 Giáo sinh : Bùi Văn Long Giáo viên hướng dẫn : Hoàng Đức Thịnh Muốn chứng minh đường thẳng d vuông góc với một mặt phẳng ( ) ta phải làm thế nào ? Bước 1: Chọn hai đường thẳng a và b cắt nhau thuộc mp ( ) Bước 2: Cm: Hoặc CM d // với đường thẳng nào đó vuông góc với mp ( ) Kiểm tra bài cũ Tiết 34: ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG ( Tiếp theo ) - Góc giữa đường thẳng và mặt phẳng . - Định nghĩa và các tính chất của phép chiếu vuông góc . - Định lí ba đường vuông góc Nội dung bài học - Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng 3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng Tính chất 1. Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại . Hai đt phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau . Tính chất 2. Đt nào vuông góc với một trong hai mp song song thì vuông góc với mp còn lại . Hai mp phân biệt cùng vuông góc với một đt thì song song với nhau . a P a b P Q Cho đường thẳng a // b, mp (P). Nếu a (P) thì b và mp (P) như thế nào ? Nếu a và b cùng vuông góc với mp (P) thì a và b như thế nào ? 3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng Tính chất 3. Cho đt a và mp(P ) song song với nhau . Đt nào vuông góc với (P) thì cũng vuông góc với a. Nếu một đt và một mặt phẳng ( không chứa đt đó ) cùng vuông góc với một đt thì chúng song song với nhau . a P b a’ Xét phép chiếu song song lên mặt phẳng ( α ) theo phương vuông góc với mặt phẳng ( α ) ) α 4. Định lí ba đường vuông góc M Nhắc lại phép chiếu song song ? -( α ) là mp chiếu - là phương chiếu -M’ là hình chiếu song song của M qua phép chiếu song song trên . 4. Định lí ba đường vuông góc A. Phép chiếu vuông góc Phép chiếu song song lên mặt phẳng ( ) theo phương vuông góc với mặt phẳng ( ) gọi là phép chiếu vuông góc lên mặt phẳng ( ). ) P M Chú ý : ● Khi M (P) thì M M’ ● Phép chiếu vuông góc có mọi tính chất của phép chiếu song song . ● Phép chiếu vuông góc lên (P) còn gọi là phép chiếu lên (P). B. Định lí ba đường vuông góc -Cho đường thẳng a không nằm trong mp (P). Hãy xác định hình chiếu a’ của đường thẳng a trên (P). Hoạt động 1: ) P a A B B’ A’ a’ - Là đường thẳng a’ Trả lời : ) P a b A B B’ A’ a’ Hoạt động 2: Với đường thẳng b nằm trong (P). CM nếu b vuông góc với a. Suy ra b vuông góc với a’ và ngược lại . Trả lời : b a và b AA’ thì b ( a,a ’) do đó , b a’. b a’ và b AA’ thì b ( a.a ’) do đó,b a. ● Nếu a nằm trong (P) thì điều trên còn đúng không ? ● Nếu a (P) thì hình chiếu của a là a nên kết quả trên là đúng Chú ý : Định lí 2: Cho đt a không vuông góc với (P), đt b nằm trong (P). Điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P). CM: ( Về nhà hoàn thiện ) Ví dụ : Cho hình chóp S.ABCD có đáy là hình vuông . SA (ABCD). CM: BD SC. Cm: Ta có : BD AC (do ABCD là hv ). BD SA (do SA (ABCD)). BD SC. ( đpcm ) S A B C D Định nghĩa : - Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng : Góc giữa đt a và mp (P) bằng 90 . - Nếu đt a không vuông góc với mp (P) thì góc giữa a và hình chiếu a’ của nó trên (P) gọi là góc giữa đt a và mp (P). 5. Góc giữa đường thẳng và mặt phẳng 0 P P a a A A’ I a’ Lưu ý: Góc giữa đường thẳng và mp không vượt quá 90 0 a P XĐ giao điểm M của a với (P) Chọn A a khác M, sao cho dễ XĐ chân vuông góc H của A tới (P). XĐ hình chiếu H của A – Tìm được a’. Góc giữa a, a’ cần tìm . A a’ H PP CHUNG XĐ GÓC GiỮA ĐƯỜNG VÀ MẶT ? M Câu 1. Góc giữa đường thẳng SD và mp(ABCD ) là : Góc ASD Góc SDA Góc SDB Góc SDC s d c b a Ví dụ : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với mặt phẳng (ABCD) và SA = a 6 . Câu 2 . Góc giữa đường thẳng SC và mp(ABCD ) là : Góc ASC Góc SCD Góc SCB Góc SCA Câu 3 . Tính góc giữa : đt SC và mp (ABCD); đt SC và mp (SAB); đt SB và mp (SAC); đt AC và mp (SBC); s d c b a Ví dụ : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với mặt phẳng (ABCD) và SA = a 6 . O K Bài học đến đây là hết Xin cảm ơn quý thầy cô giáo và các em học sinh! Chúc sức khỏe
File đính kèm:
 bai_giang_hinh_hoc_lop_11_tiet_34_duong_thang_vuong_goc_voi.ppt
bai_giang_hinh_hoc_lop_11_tiet_34_duong_thang_vuong_goc_voi.ppt

