Bài giảng Hình học Lớp 11 - Chương 3 - Bài 3: Đường thẳng vuông góc với mặt phẳng
Bài toán:
Cho hai đường thẳng cắt nhau b và c cùng nằm trong mặt phẳng (P). Chứng minh rằng nếu a vuông góc với b và c thì nó vuông góc với mọi đường thẳng nằm trong (P)
Vậy:
Đt(a) vuông góc với đt(d). Do d là đường thẳng bất kỳ trong (P) nên có đpcm
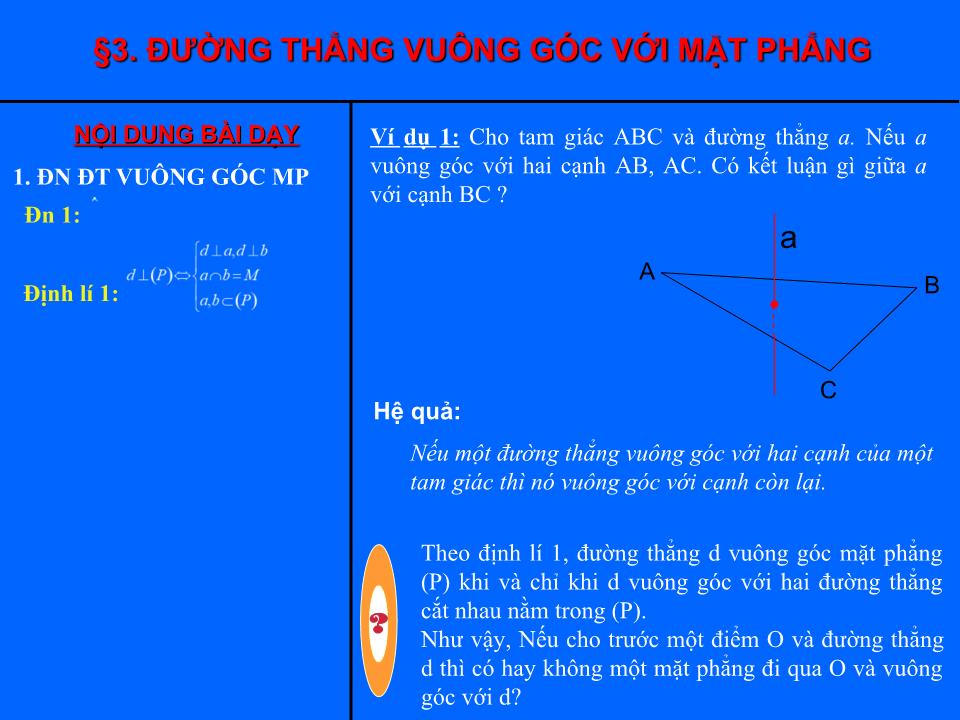
ĐỊNH NGHĨA 1
Một đường thẳng gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
ĐỊNH LÍ 1
Từ bài toán mở đầu, để cm đt vuông góc với mp ta cần cm điều gì ?
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P).

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 11 - Chương 3 - Bài 3: Đường thẳng vuông góc với mặt phẳng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 11 - Chương 3 - Bài 3: Đường thẳng vuông góc với mặt phẳng

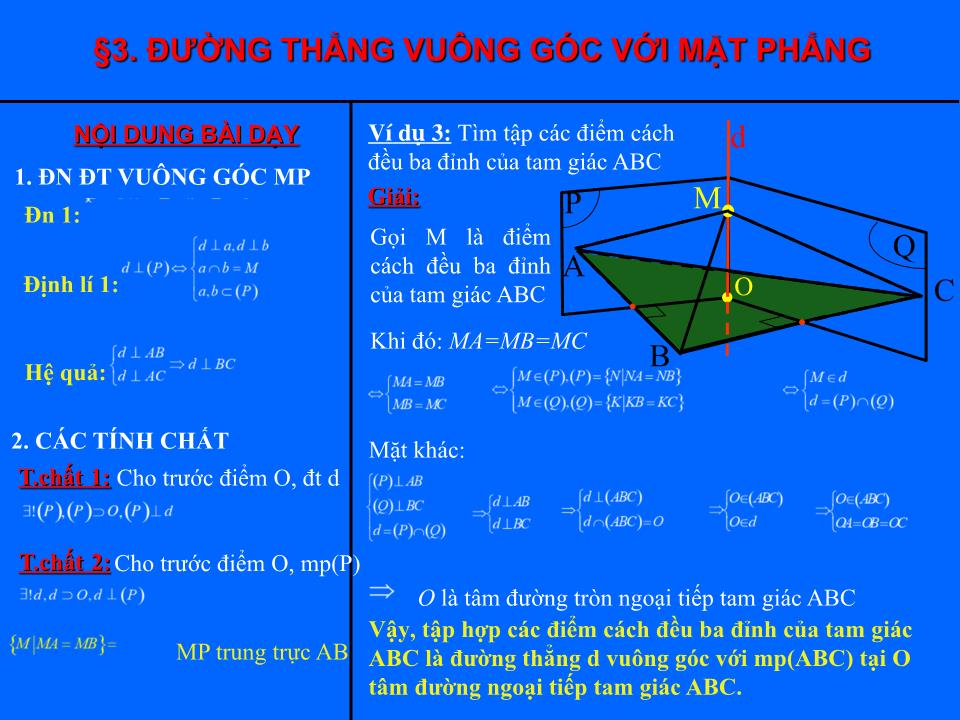
KIỂM TRA BÀI CŨ 1. a) b) 2. §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG Bài toán : Cho hai đường thẳng cắt nhau b và c cùng nằm trong mặt phẳng (P). Chứng minh rằng nếu a vuông góc với b và c thì nó vuông góc với mọi đường thẳng nằm trong (P) a P c b d CM: Do 3 véc tơ đồng phẳng nên vì Vậy : Đt(a ) vuông góc với đt(d ). Do d là đường thẳng bất kỳ trong (P) nên có đpcm Cho đt (d) bất kỳ trong mặt phẳng (P) KIẾN THỨC §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG 1. Định nghĩa đường thẳng vuông góc với mặt phẳng ĐỊNH NGHĨA 1 Một đường thẳng gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó . ĐỊNH LÍ 1 Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P). Chú ý: Đường thẳng d vuông góc mặt phẳng (P), ta còn nói mặt phẳng (P) vuông góc với đường thẳng d hoặc d và (P) vuông góc với nhau . Tức là : NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Từ bài toán mở đầu , để cm đt vuông góc với mp ta cần cm điều gì ? ? §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG Ví dụ 1: Cho tam giác ABC và đường thẳng a. Nếu a vuông góc với hai cạnh AB, AC. Có kết luận gì giữa a với cạnh BC ? A B C a Hệ quả : Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó vuông góc với cạnh còn lại . Theo định lí 1, đường thẳng d vuông góc mặt phẳng (P) khi và chỉ khi d vuông góc với hai đường thẳng cắt nhau nằm trong (P). Như vậy , Nếu cho trước một điểm O và đường thẳng d thì có hay không một mặt phẳng đi qua O và vuông góc với d? ? NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: P §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : O d b a Ta thấy , từ một điểm O ta có thể dựng được các đường thẳng a, b đi qua O và vuông góc với d. Khi đó , ta xác định được mp(P ) đi qua a, b Theo định lí 1, Như vậy , tồn mp(P ) đi qua O và vuông góc với d Giả sử , có mp (Q) cũng đi qua O và (Q) vuông góc với d Khi đó : ( Không xẩy ra ) §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : Có duy nhất một mặt phẳng (P) đi qua điểm O cho trước và vuông góc với đường thẳng a đã cho . Tính chất 1 P O a Vấn đề đặt ra : Cho trước một điểm O và một mặt phẳng (P). Liệu có hay không một đường thẳng đi qua O và vuông góc với mặt phẳng (P)? ? 2. CÁC TÍNH CHẤT §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : Ta thấy , khi cho trước một điểm O và một mặt phẳng (P). Khi đó , đường thẳng d đi qua O, d vuông góc với (P) tại H. P O H d K c Giả sử , có đt c ( khác đt d) đi O và c vuông góc với (P) tại K. Ta có : Vậy tổng 3 góc của tg OHK lớn hơn 180 o Suy ra : Có duy nhất đường thẳng d đi qua điểm O cho trước và vuông góc với mặt phẳng (P) cho trước . Tính chất 2 Trong (P), lấy hai đường thẳng cắt nhau a và b. 2. CÁC TÍNH CHẤT T.chất 1: Cho trước điểm O, đt d Q R a b Dựng hai mp (Q), (R) đi qua O và lần lượt vuông góc với hai đường thẳng a, b. Dựng giao tuyến d của hai mp (Q) và (R). §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) NHẬN XÉT: 1. Cho trước điểm O và đt d. Mặt phẳng (P) đi qua điểm O và vuông góc với đt d chính là mp đi qua hai đường thẳng cắt nhau tại O và cùng vuông góc với d P O d b a 2. Cho trước mp(p ) và điểm O. Đường thẳng d đi qua điểm O và vuông góc với mặt phẳng (P) chính là giao tuyến của hai mp đi qua O và lần lượt vuông góc với hai đt cắt nhau nằm trong mp(P ). P O H d Q R a b 3. Từ tính chất 1, ta thấy có duy nhất một mp vuông góc với AB tại trung điểm O của đoạn thẳng AB. Mặt phẳng đó gọi là mp trung trực của đoạn thẳng AB. Dễ thấy , Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng . MP trung trực AB §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB Ví dụ 3: Tìm tập các điểm cách đều ba đỉnh của tam giác ABC P A B C Q d M O Giải : Gọi M là điểm cách đều ba đỉnh của tam giác ABC Khi đó : MA=MB=MC Mặt khác : O là tâm đường tròn ngoại tiếp tam giác ABC Vậy , tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mp(ABC ) tại O tâm đường ngoại tiếp tam giác ABC. §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB Tập hợp các điểm cách đều ba đỉnh của tam giác ABC được gọi trục đường tròn ngoại tiếp tam giác ABC A B C d M O (O là tâm đường tròn ngoại tiếp tam giác ABC) Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: b. Chứng minh rằng : BC (SAB) c. Gọi H là hình chiếu của A lên SB. Chứng minh rằng AH (SBC) Cho hình chóp tam giác S.ABC có SA (ABC), ∆ ABC vuông tại B. a. Chứng minh : ∆ SA B, ∆ SA C là các tam giác vuông . a B c s H Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB BÀI TẬP ÁP DỤNG Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: a B c s H a. Chứng minh : SA B, SA C là các tam giác vuông b. Chứng minh rằng : BC (SAB) Từ (1) vaø (2), suy ra : BC (SAB) BC AB (1) BC SA (2) ABC vuông tại B SA (ABC) c. Chứng minh rằng : AH (SBC) Töø (3) vaø (4), suy ra : AH (SBC) AH SB (3) AH BC (4) H là hình chiếu của A lên SB SAB vuông tại A SAC vuông tại A BC (SAB) ^ AH (SAB) Ì Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB Qua bài tập áp dụng ở trên em hãy cho biết “ Phương pháp để chứng minh một đường thẳng vuông góc với một mặt phẳng ”? ? Để chứng minh một đương thẳng vuông góc với một mặt phẳng , ta đi chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau cùng nằm trong mặt phẳng đó . Tức là : Qua nội dung bài học hôm nay, ta có thêm một phương pháp chứng minh hai đường thẳng vuông góc với nhau . Em hãy cho biết đó là phương pháp nào ? ? Để chứng minh hai đường thẳng vuông góc với nhau , ta đi chứng minh đương thẳng này vuông góc với một mặt phẳng chứa đương thẳng kia . Tức là : Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác §3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI DẠY 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d Cho trước điểm O, mp(P ) MP trung trực AB BÀI TẬP TRẮC NGHIỆM Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác CỦNG CỐ NỘI DUNG BÀI HỌC 1. ĐN ĐT VUÔNG GÓC MP Đn 1: Định lí 1: Hệ quả : 2. CÁC TÍNH CHẤT T.chất 2: T.chất 1: Cho trước điểm O, đt d. Cho trước điểm O, mp(P ). Mặt phẳng trung trực của đoạn thẳn AB TRI THỨC PHƯƠNG PHÁP 1. Phương pháp chứng minh đường thẳng d vuông góc mặt phẳng (P): 2. Phương pháp chứng minh đường thẳng a vuông góc đường thẳng b: Tập hợp tất cả các điểm cách đều 3 đỉnh của tam giác là đt đi qua tâm đường tròn ngoại tiêp của tam giác và vuông góc với mp tam gác BÀI TẬP VỀ NHÀ Các em về nhà học bài và làm tập 16, 18/ SGK. Xem trước các nội dung: Liên hệ giữa quan hệ song song và quan hệ của đường thẳng và mặt phẳng ; Định lí 3 đường vuông góc ; Góc giữa đường thẳng và mặt phẳng .
File đính kèm:
 bai_giang_hinh_hoc_lop_11_chuong_3_bai_3_duong_thang_vuong_g.ppt
bai_giang_hinh_hoc_lop_11_chuong_3_bai_3_duong_thang_vuong_g.ppt

