Bài giảng Hình học Lớp 11 - Chương 2: Quan hệ song song - Tiết 21: Đường thẳng và mặt phẳng song song
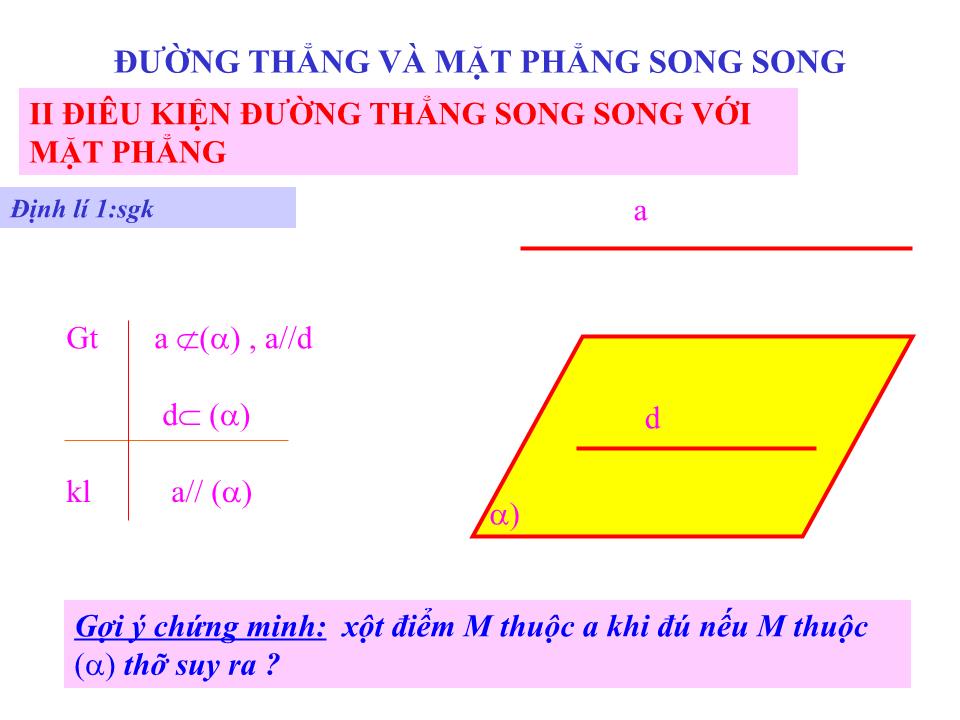
Gợi ý chứng minh: xột điểm M thuộc a khi đú nếu M thuộc () thỡ suy ra ?
CÁC TÍNH CHẤT
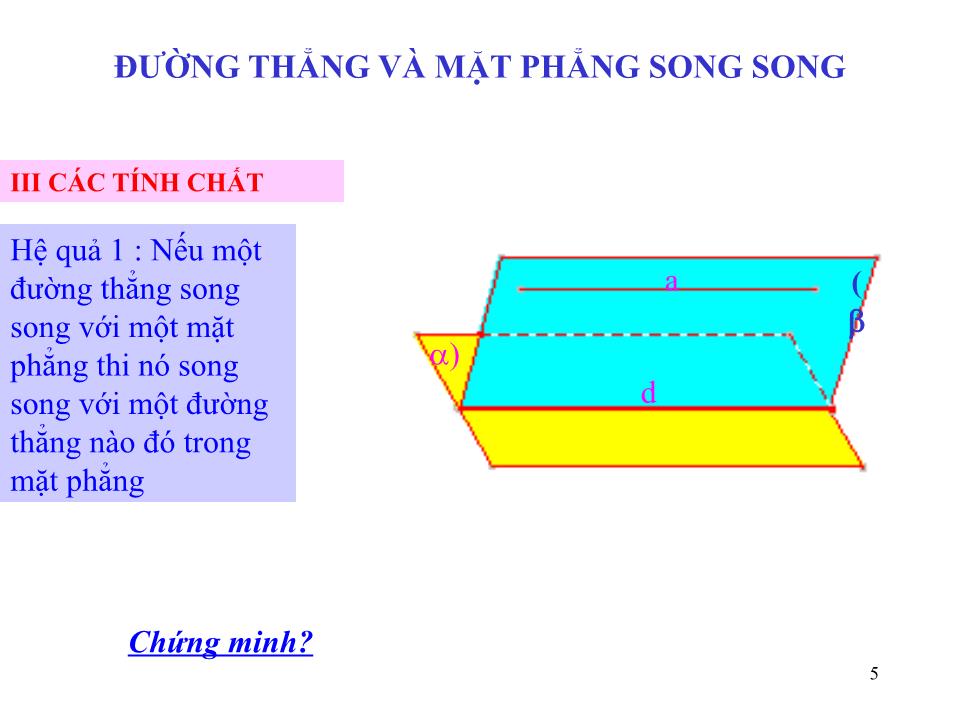
Hệ quả 1 : Nếu một đường thẳng song song với một mặt phẳng thi nó song song với một đường thẳng nào đó trong mặt phẳng
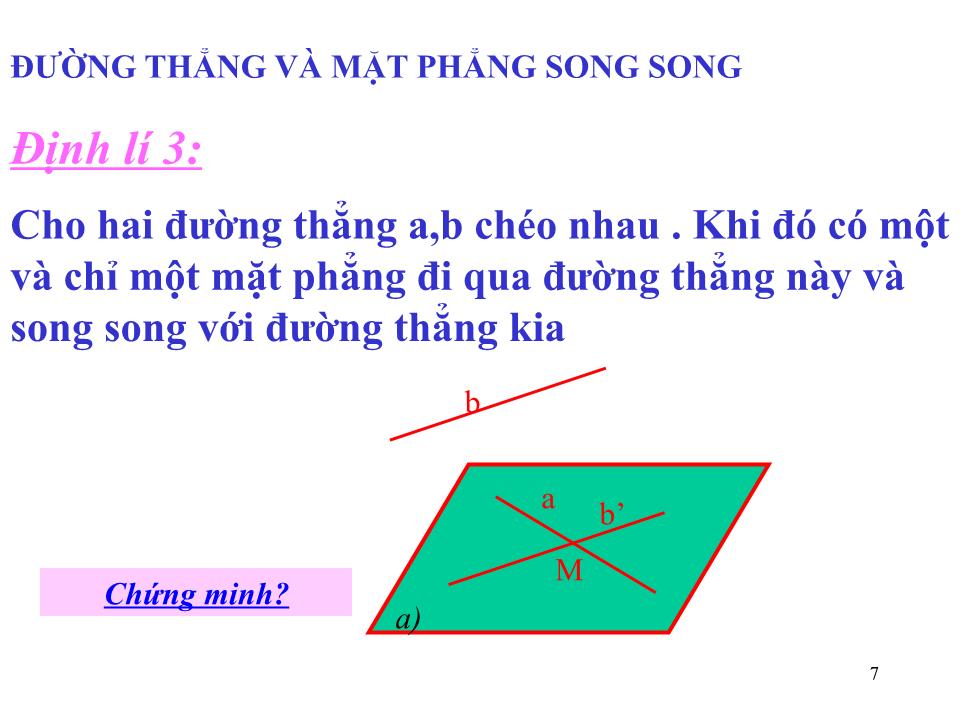
Định lí 3:
Cho hai đường thẳng a,b chéo nhau . Khi đó có một và chỉ một mặt phẳng đi qua đường thẳng này và song song với đường thẳng kia
ÁP DỤNG ĐỊNH LÍ 1:
MUỐN CHỨNG MINH MỘT ĐƯỜNG THẲNG SONG SONG VỚI MỘT MẶT PHẲNG TA CHỨNG MINH ĐỪƠNG THẲNG ĐÓ SONG SONG VỚI MỘT ĐƯỜNG THẲNG BẤT KÌ NẰM TRONG MẶT PHẲNG.
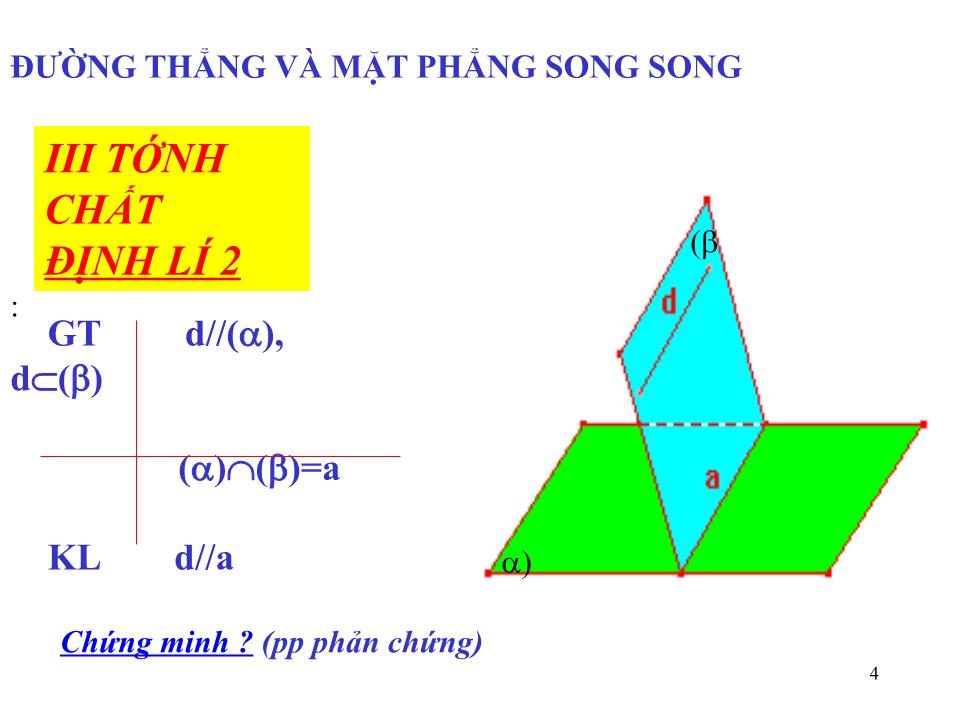
ÁP DỤNG ĐỊNH LÍ 2 :
MUỐN TÌM GIAO TUYẾN HAI MẶT PHẲNG () V À () CỰNG CHỨA ĐƯỜNG THẲNG D SONG SONG () .
+)TÌM MỘT ĐIỂM CHUNG CỦA HAI MẶT PHẲNG
+) GIAO TUYẾN ĐI QUA ĐIỂM CHUNG VÀ SONG SONG VỚI D.

Trang 1
Trang 2
Trang 3
Trang 4
Trang 5
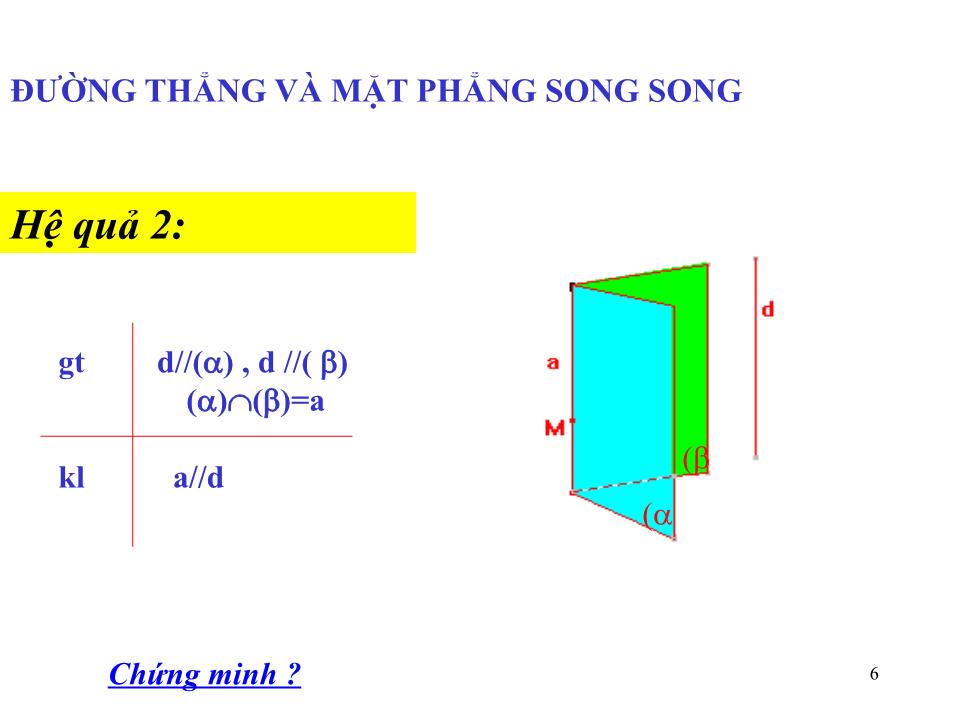
Trang 6
Trang 7

Trang 8
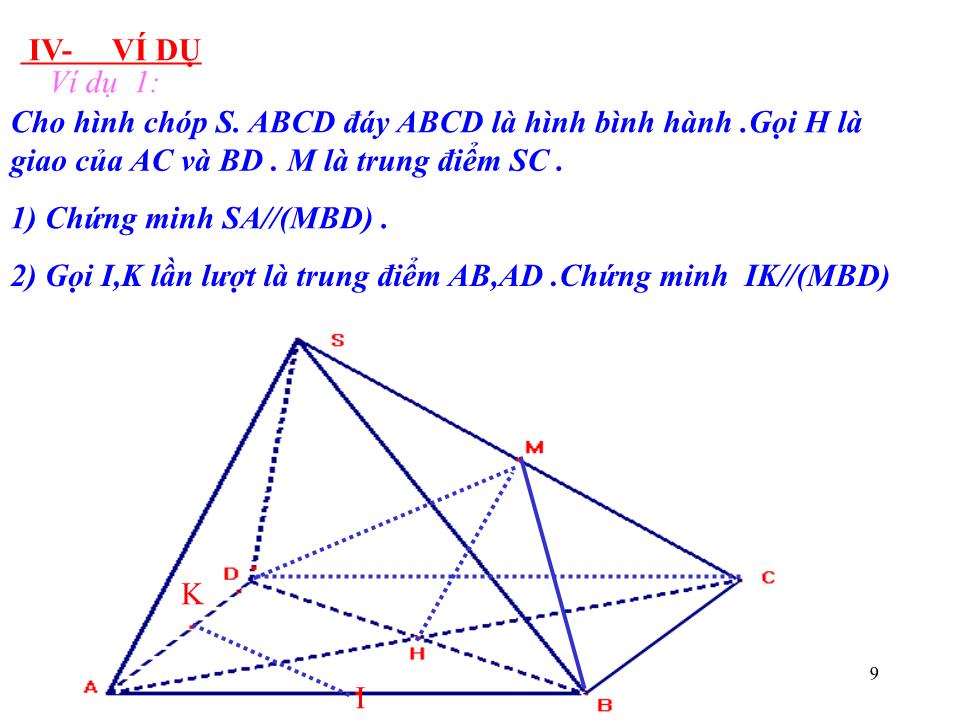
Trang 9
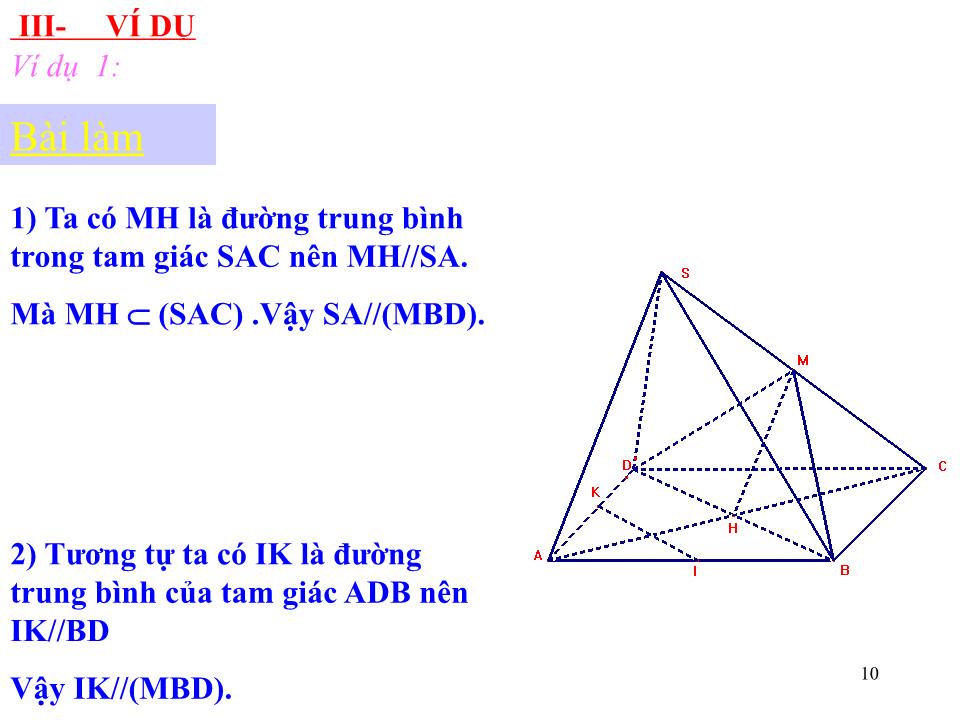
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 11 - Chương 2: Quan hệ song song - Tiết 21: Đường thẳng và mặt phẳng song song

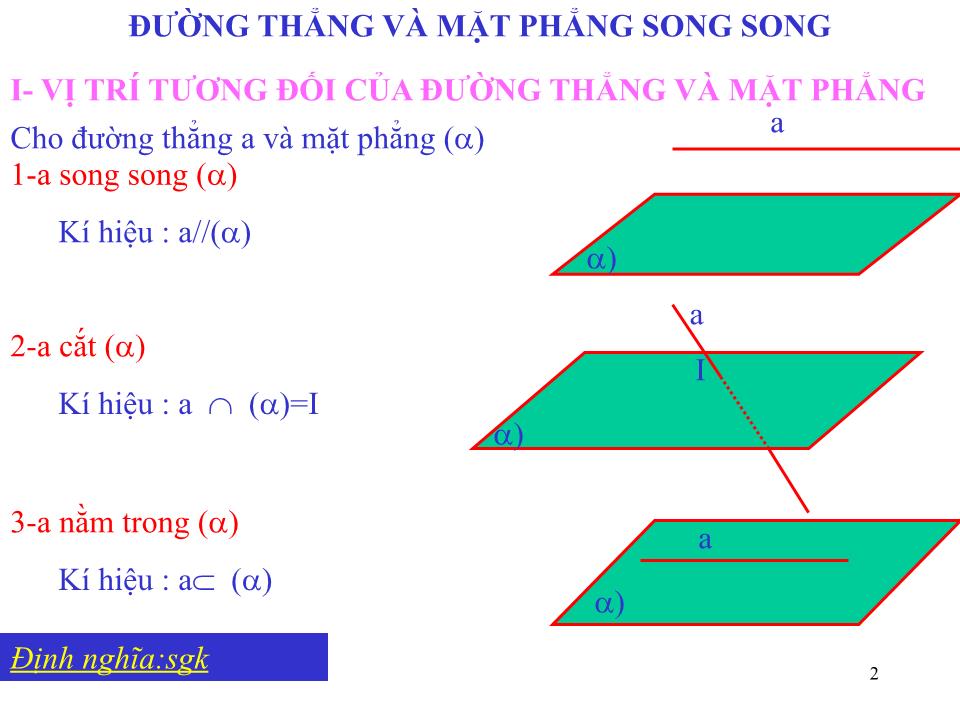
1 CH ƯƠ NG II. Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG . TO ÁN 11 N  NG CAO (tiết 20&21) TI ẾT 20 : HỌC LÍ THUYẾT TIẾT 21 : LÀM BÀI TẬP TRƯỜNG THPT THẠCH THẤT ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG BÀI GIÁO VIÊN : KHUẤT ĐÌNH CẢI 2 Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG I- VỊ TRÍ T ƯƠ NG ĐỐI CỦA Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG Cho đ ư ờng thẳng a và mặt phẳng ( ) 1-a song song ( ) Kí hiệu : a//( ) a ) 2-a cắt ( ) Kí hiệu : a ( )=I 3-a nằm trong ( ) Kí hiệu : a ( ) Định nghĩa:sgk ) a ) a I 3 Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG II ĐIÊU KIỆN Đ Ư ỜNG THẲNG SONG SONG VỚI MẶT PHẲNG Định lí 1:sgk Gt a ( ) , a//d d ( ) kl a// ( ) ) a d Gợi ý chứng minh: xột điểm M thuộc a khi đú nếu M thuộc ( ) thỡ suy ra ? 4 III TỚNH CHẤT ĐỊNH LÍ 2 GT d//( ), d ( ) ( ) ( )=a KL d//a : Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG ) ( Chứng minh ? (pp phản chứng) 5 Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG III CÁC TÍNH CHẤT Hệ quả 1 : Nếu một đường thẳng song song với một mặt phẳng thi nó song song với một đường thẳng nào đó trong mặt phẳng ( ) d Chứng minh? a 6 Hệ quả 2: gt d//( ) , d //( ) ( ) ( )=a kl a//d Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG ( ( Chứng minh ? 7 Định lí 3: Cho hai đ ư ờng thẳng a,b chéo nhau . Khi đó có một và chỉ một mặt phẳng đi qua đ ư ờng thẳng này và song song với đ ư ờng thẳng kia Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG a b b’ M a) Chứng minh? 8 Định lí 1 :Nếu một đ ư ờng thẳng d không nằm trên mặt phẳng ( ) và song song với một đ ư ờng thẳng a nào đó nằm trên ( ) thì đ ư ờng thẳng d song song với mặt phẳng ( ) . Định lí 2 : Cho đ ư ờng thẳng d song song với mặt phẳng ( ).Nếu mặt phẳng () đi qua d và cắt mặt phẳng ( ) thì giao tuyến của ( ) và () song song với d. H ệ quả : Nếu hai mặt phẳng cắt nhau và cùng song song với một đ ư ờng thẳng thì giao tuyến của chúng song song với đ ư ờng thẳng đó. Định lí4 : Cho hai đ ư ờng thẳng a,b chéo nhau . Khi đó có một và chỉ một mặt phẳng đi qua đ ư ờng thẳng này và song song với đ ư ờng thẳng kia TÓM TẮT KIẾN THỨC CẦN NHỚ VỀ §êng th¼ng vµ mÆt ph¼ng song song ÁP DỤNG ĐỊNH LÍ 1: MUỐN CHỨNG MINH MỘT Đ Ư ỜNG THẲNG SONG SONG VỚI MỘT MẶT PHẲNG TA CHỨNG MINH ĐỪ Ơ NG THẲNG ĐÓ SONG SONG VỚI MỘT Đ Ư ỜNG THẲNG BẤT KÌ NẰM TRONG MẶT PHẲNG. ÁP DỤNG ĐỊNH LÍ 2 : MUỐN TÌM GIAO TUYẾN HAI MẶT PHẲNG ( ) V À () CỰNG CHỨA Đ Ư ỜNG THẲNG D SONG SONG ( ) . +)TÌM MỘT ĐIỂM CHUNG CỦA HAI MẶT PHẲNG +) GIAO TUYẾN ĐI QUA ĐIỂM CHUNG VÀ SONG SONG VỚI D. 9 Ví dụ 1: Cho hình chóp S. ABCD đáy ABCD là hình bình hành .Gọi H là giao của AC và BD . M là trung điểm SC . 1) Chứng minh SA//(MBD) . 2) Gọi I,K lần l ư ợt là trung điểm AB,AD .Chứng minh IK//(MBD) IV- VÍ DỤ K I 10 III- VÍ DỤ Ví dụ 1: Bài làm 1) Ta có MH là đ ư ờng trung bình trong tam giác SAC nên MH//SA. Mà MH (SAC) .Vậy SA//(MBD). 2) T ươ ng tự ta có IK là đ ư ờng trung bình của tam giác ADB nên IK//BD Vậy IK//(MBD). 11 . . . . . . . E H G F M III-VÍ DỤ Cho tứ diện ABCD. Gọi M là một điểm nằm trong tam giác ABC, ( ) là mặt phẳng đi qua M và song song với các đ ư ờng thẳng AB và CD . Hãy tìm thiết diện của mặt phẳng ( ) với tứ diện ABCD. Thiết diện là hình gì? Ví dụ 2: 12 Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG III-VÍ DỤ Ví dụ 2: Giải: Vì ( ) và (ABC) có điểm Mchung và ( )//AB nên giao tuyến của chúng qua M song song AB cắt BC tại F cắt AC tại E vậy E F nằm trên ( ) .T ươ ng tự ( ) và (ACD) có chung điểm E ( ) //CD nên giao tuyến của chúng qua E song song CD cắt AD tại H . ( ) và (ABD ) chung điểm H ( ) //AB nên giao tuyến qua H song song AB cắt BD tại G Hình bình hành E FGH là thiết diện cần tìm 13 14 N M P Q VD 3: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi . Gọi O là giao điểm của hai đ ư ờng chéo AC và BD .Xác định thiết diện của hình chóp cắt bởi mặt phẳng ( ) đi qua O ,song song với AB và SC . Thiết diện đó là hình gì ? 15 Ví dụ 3 (b ài 27) Bài làm: Đ Ư ỜNG THẲNG VÀ MẶT PHẲNG SONG SONG V ì mặt phẳng ( ) và mặt phẳng (ABCD) có chung điểm O mà ( ) //AB nên giao tuyến của chúng đi qua O song song AB cắt AD tại N, cắt BC tại M .T ươ ng tự ( ) và (SBC) có chung điểm M và ( ) //SC nên giao tuyến qua M song song AC cắt SB tại Q.Vì ( ) và (SAB) có chung điểm Q , ( ) //AB nên giao tuyến qua Q song song AB cắt SA tại P .Hình thang MNPQ là thiết diện cần tìm. 16 Bài tập Cho hỡnh chúp SABCD đỏy ABCD là hỡnh thang với AB//CD ;gọi G, G’ lần lượt là trọng tõm tam giỏc SAD, SBC. Chứng minh đường thẳng GG’ song song với mặt phẳng (SAB). 17 S A B C D I K G G’ CHÂN THÀNH CÁM ƠN CÁC THẦY GIÁO, CÔ GIÁO VÀ CÁC EM HỌC SINH 11A1
File đính kèm:
 bai_giang_hinh_hoc_lop_11_chuong_2_quan_he_song_song_tiet_21.ppt
bai_giang_hinh_hoc_lop_11_chuong_2_quan_he_song_song_tiet_21.ppt

