Bài giảng Hình học Lớp 11 - Chương 2 - Bài 4: Hai mặt phẳng song song
ĐỊNH NGHĨA
Hai mặt phẳng được gọi là song song với với nhau, nếu chúng không có điểm chung.
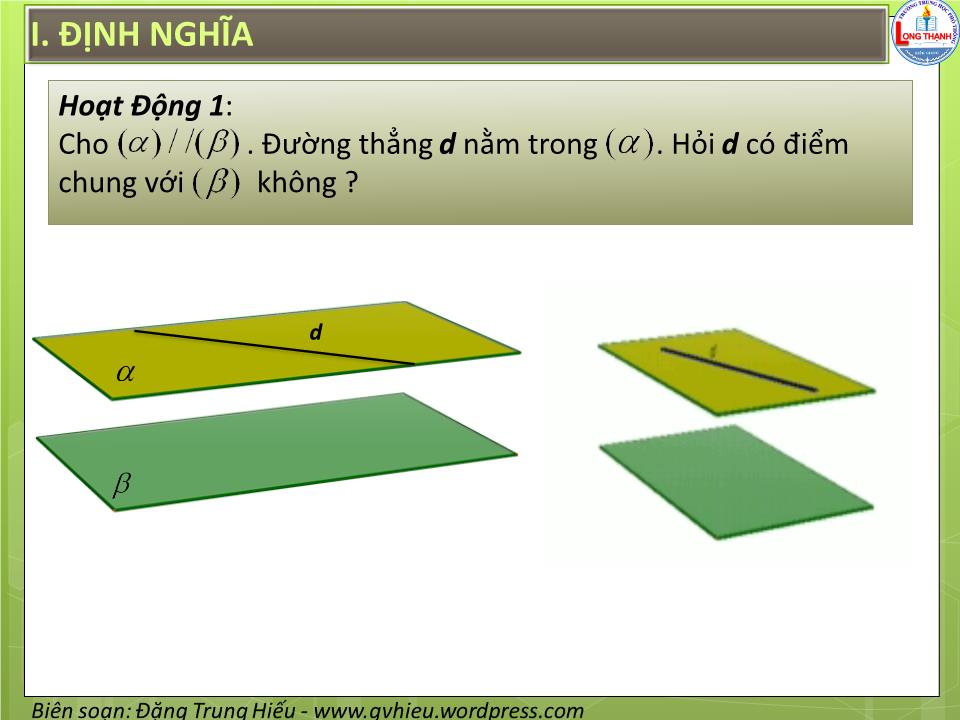
Hoạt Động 1:
Cho . Đường thẳng d nằm trong . Hỏi d có điểm chung với không ?
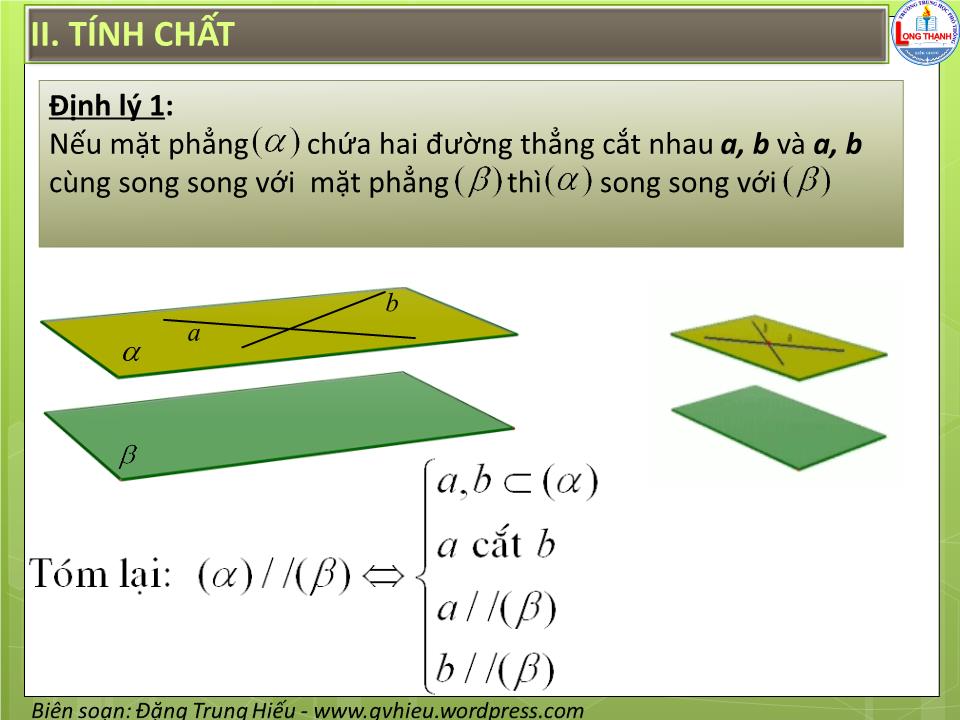
Định lý 1:
Nếu mặt phẳng chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng thì song song với

Trang 1

Trang 2
Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Hình học Lớp 11 - Chương 2 - Bài 4: Hai mặt phẳng song song", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Hình học Lớp 11 - Chương 2 - Bài 4: Hai mặt phẳng song song

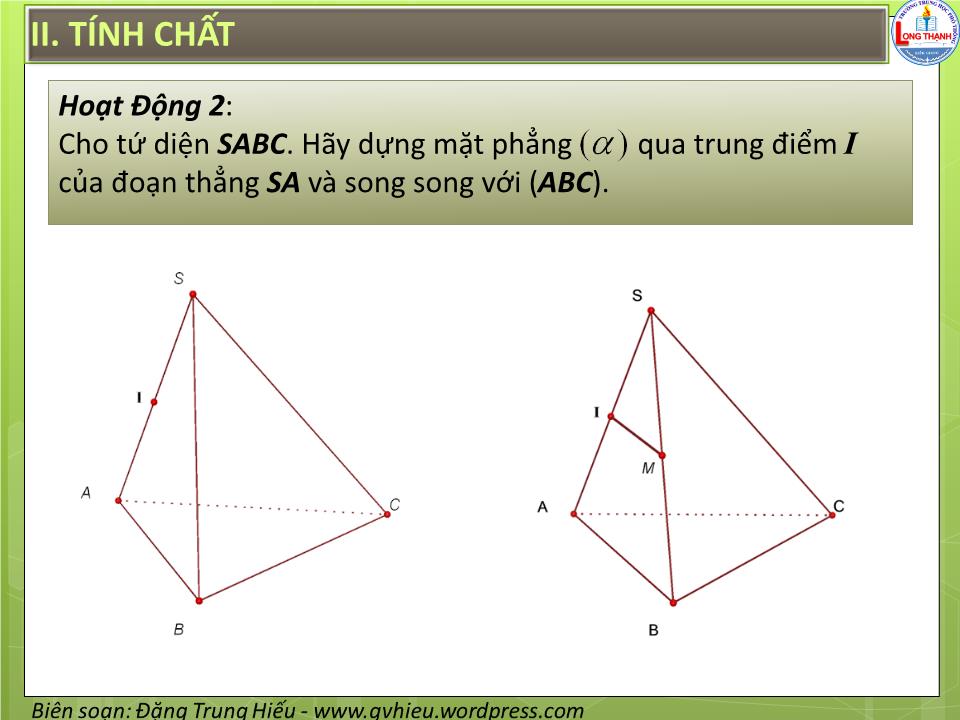
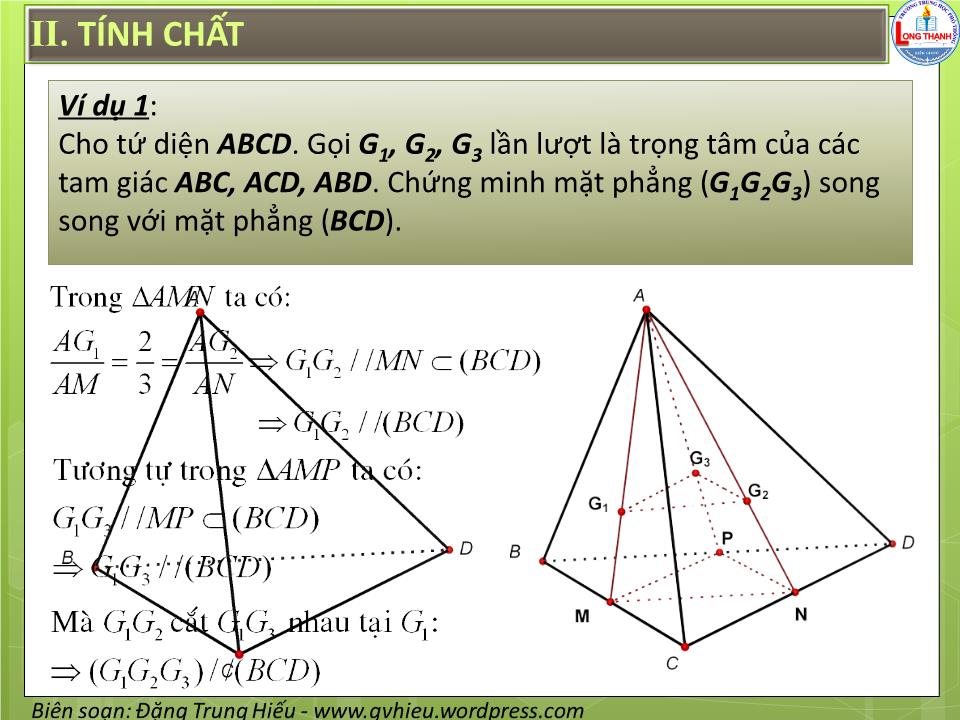
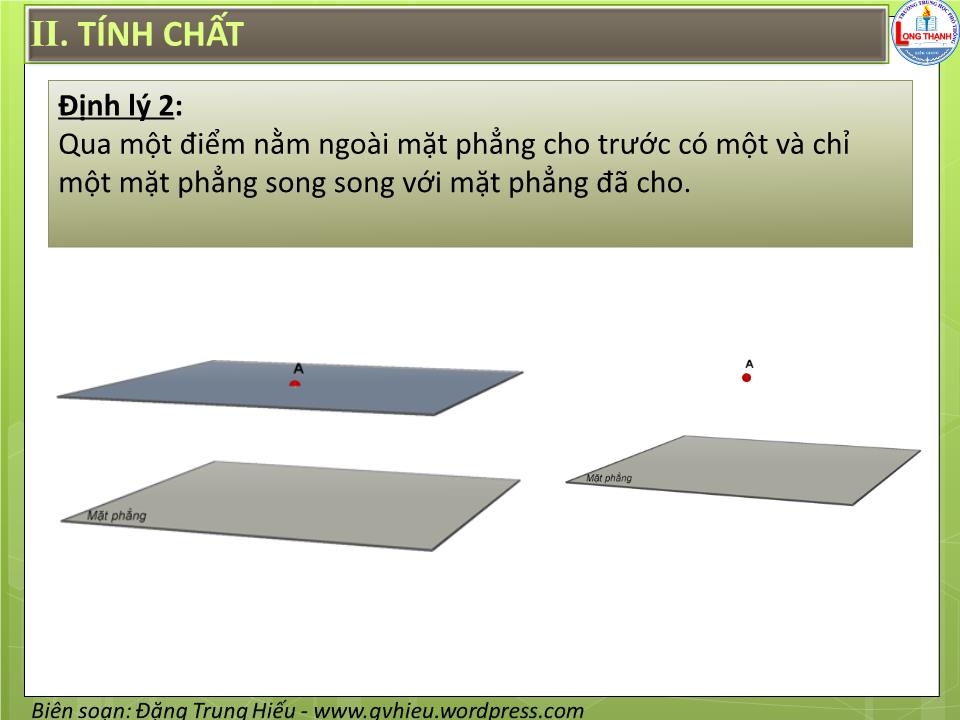
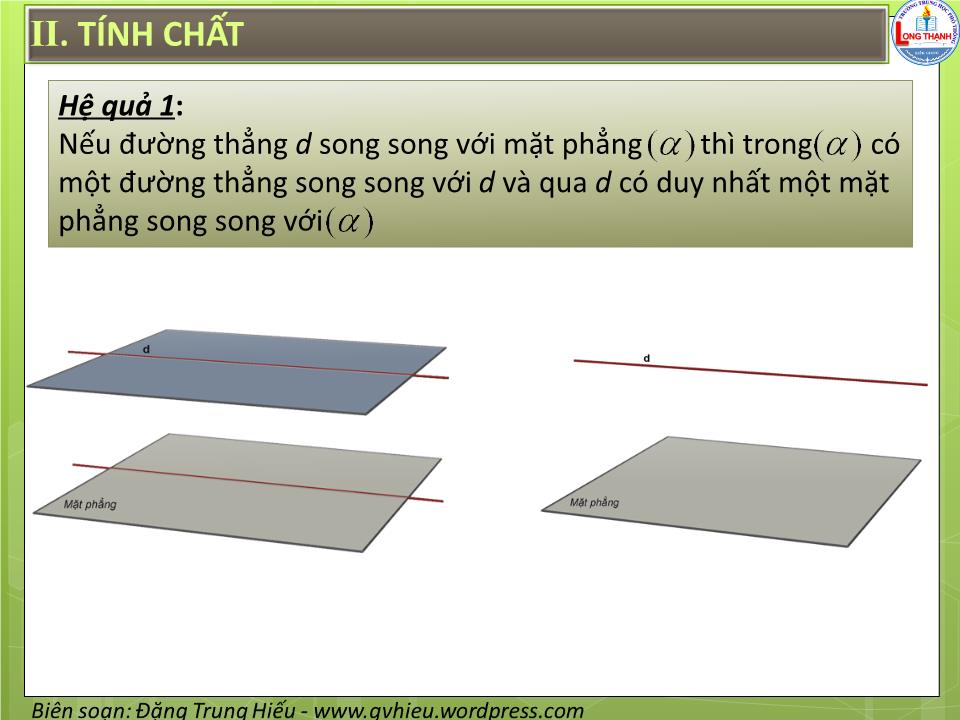
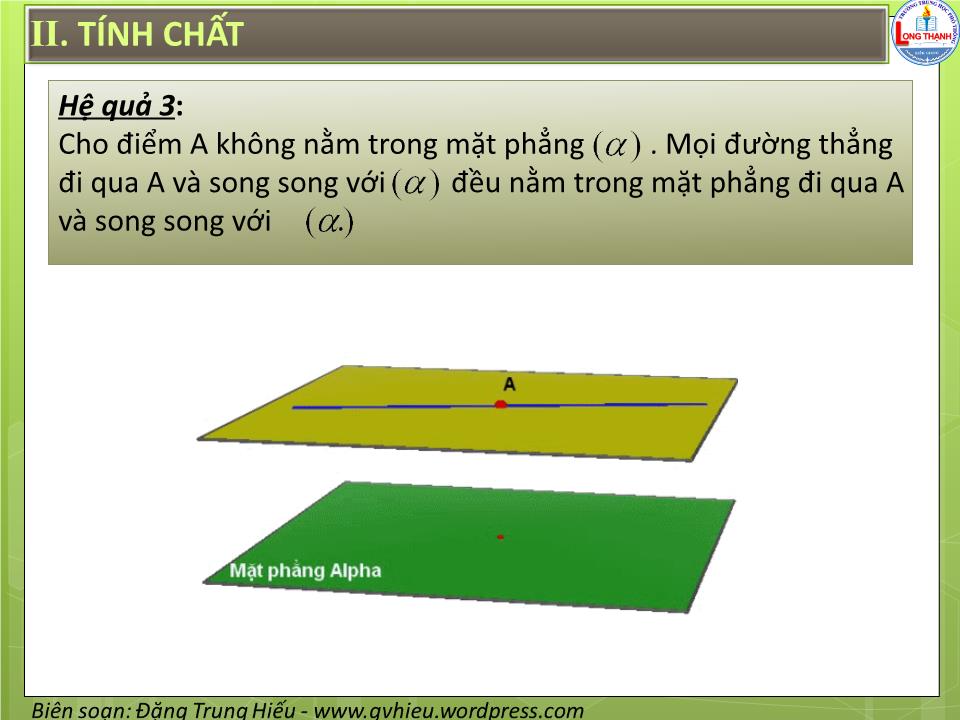
§4. HAI MẶT PHẲNG SONG SONG I. ĐỊNH NGHĨA Hai mặt phẳng được gọi là song song với với nhau, nếu chúng không có điểm chung. I. ĐỊNH NGHĨA Hoạt Động 1 : Cho . Đường thẳng d nằm trong . Hỏi d có điểm chung với không ? d II. TÍNH CHẤT Định lý 1 : Nếu mặt phẳng chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng thì song song với a b II. TÍNH CHẤT Hoạt Động 2 : Cho tứ diện SABC . Hãy dựng mặt phẳng qua trung điểm I của đoạn thẳng SA và song song với ( ABC ). II . TÍNH CHẤT Ví dụ 1 : Cho tứ diện ABCD . Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm của các tam giác ABC, ACD, ABD . Chứng minh mặt phẳng ( G 1 G 2 G 3 ) song song với mặt phẳng ( BCD ). II . TÍNH CHẤT Định lý 2 : Qua một điểm nằm ngoài mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho. II . TÍNH CHẤT Hệ quả 1 : Nếu đường thẳng d song song với mặt phẳng thì trong có một đường thẳng song song với d và qua d có duy nhất một mặt phẳng song song với II . TÍNH CHẤT Hệ quả 2 : Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau. II . TÍNH CHẤT Hệ quả 3 : Cho điểm A không nằm trong mặt phẳng . Mọi đường thẳng đi qua A và song song với đều nằm trong mặt phẳng đi qua A và song song với . II . TÍNH CHẤT Định lý 3 : Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau. II . TÍNH CHẤT Hệ quả : Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau. II . ĐỊNH LÝ TA – LÉT (THALÈS) Định lý 4 : Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ. IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP Hình lăng trụ IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP Lăng trụ tam giác Lăng trụ tứ giác Lăng trụ lục giác IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP Khi đáy là hình bình hành, thì hình lăng trụ được gọi là hình hộp Hình hộp V. HÌNH CHÓP CỤT Tính chất: 1) Hai đáy là hai đa giác có các cặp cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau 2) Các mặt bên là những hình thang. 3) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm BÀI TẬP VỀ NHÀ VỀ NHÀ LÀM BÀI TẬP 2,3,4
File đính kèm:
 bai_giang_hinh_hoc_lop_11_chuong_2_bai_4_hai_mat_phang_song.ppt
bai_giang_hinh_hoc_lop_11_chuong_2_bai_4_hai_mat_phang_song.ppt

