Bài giảng Đại số Lớp 12 - Tiết 82: Hàm số logarit
Định nghĩa:
Tập xác định: D =
Tập giá trị: T = R .
Ví dụ:
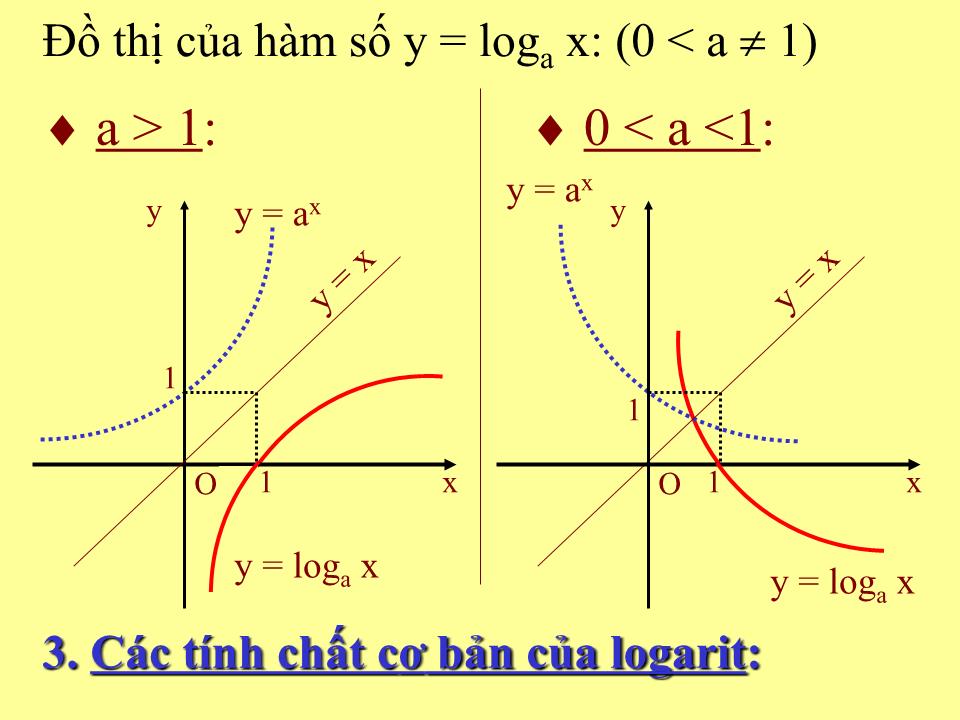
Đồ thị:
Trong hệ tọa độ Đêcac vuông góc Oxy, đồ thị của hàm số y = loga x (0 < a 1) là đối xứng với đồ thị của hàm số y = ax qua đường phân giác thứ nhất (y = x).

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Tiết 82: Hàm số logarit", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Tiết 82: Hàm số logarit

TRƯỜNG THPT ĐẶNG HUY TRỨ BAN GIÁM KHẢO CÙNG QUÝ THẦY, CÔ ĐẾN DỰ TIẾT HỌC HÔM NAY. KIỂM TRA BÀI CŨ: Câu hỏi 1: Lập bảng biến thiên của hàm số y = a x ( a > 0 và a ≠ 1) ? Câu hỏi 2: Nêu điều kiện đủ để hàm số có hàm số ng ư ợc ? Câu hỏi 3: Hàm số y = a x (a > 0 và a ≠1) có hàm số ng ư ợc không ? Tại sao ? a/ Định nghĩa : Tiết 82 : 1. Định nghĩa : Tập xác định: D = Tập giá trị: T = R . Ch ươ ng VI: HÀM SỐ LOGARIT. Bài 2:HÀM SỐ LOGARIT. a/ Định nghĩa : 1. Định nghĩa : b/ Ví dụ : b/ Ví dụ : (0 < a 1) 0 1 hàm số logarit . 2. Sự biến thiên và đồ thị : b/ Bảng biến thiín : a > 1 : 0 + 1 a 0 < a < 1 : x y = log a x - + 0 1 SKET Ch ươ ng VI: HÀM SỐ LOGARIT. Bài 2:HÀM SỐ LOGARIT. 1. Định nghĩa : 2. Sự biến thiên và đồ thị : a/ Định nghĩa : b/ Ví dụ : a/ Bảng biến thiên : c/ Đồ thị : 2. Sự biến thiên và đồ thị : b/ Bảng biến thiên: Trong hệ tọa độ Đêcac vuông góc Oxy, đồ thị của hàm số y = log a x (0 < a 1) là đối xứng với đồ thị của hàm số y = a x qua đ ư ờng phân giác thứ nhất (y = x). Ch ươ ng VI: HÀM SỐ LOGARIT. Bài 2:HÀM SỐ LOGARIT. 1. Định nghĩa : 2. Sự biến thiên và đồ thị : a/ Định nghĩa : b/ Ví dụ : SKET b/ Bảng biến thiên : c/ Đồ thị : a/ Tập xác định: a > 1 : y = a x y = x y x O 1 1 y = log a x y = log a x 0 < a <1 : y = a x x y = x y O 1 1 3. Các tính chất c ơ bản của logarit : Đồ thị của hàm số y = log a x: (0 < a 1) 4. Các định lý về logarit : a/ Định lí 1 : b/ Định lý 2 : Chú ý : Ch ươ ng VI: HÀM SỐ LOGARIT. Bài 2:HÀM SỐ LOGARIT. 1. Định nghĩa : 2. Sự biến thiên và đồ thị : 3. Các tính chất c ơ bản của logarit : 4. Các định lý về logarit : a/ Định nghĩa : b/ Ví dụ : a/ Định lí 1 : b/ Định lý 2 : a/ Bảng biến thiên : b/ Đồ thị : 2) Mở rộng: x 1 ; x 2 ; ...; x n > 0 có: BT CỦNG CỐ KIẾN THỨC: 1/ Tìm TXĐ của hàm số y = log 2 (1 - x) ? Tập xác định: D = 2/ So sánh hai số và Ta có s 0 3/ Tính giá trị của biểu thức: 4/ Tìm x biết: log 4 x 2 = 3. Ta có: log 4 x 2 = 3 x 2 = 4 3 = 64 x = 8. Đk: x ≠ 0 BÀI TẬP VỀ NHÀ: Làm bài 1 đến bài 9 trang 168, 169/SGK. BT2b TRƯỜNG THPT ĐẶNG HUY TRỨ Ban Giám khảo, quý thầy cô, cùng các em sức khoẻ và thành đạt. TRƯỜNG THPT ĐẶNG HUY TRỨ XIN CHÂN THÀNH CẢM Ơ N: - Sở GD và ĐT Thừa Thiên Huế, - Tr ư ờng THPT Quốc học Huế, - Tập thể học sinh lớp 11/3, - Cùng qúy thầy cô đã tận tình giúp đỡ để tiết dạy thành công.
File đính kèm:
 bai_giang_dai_so_lop_12_tiet_82_ham_so_logarit.ppt
bai_giang_dai_so_lop_12_tiet_82_ham_so_logarit.ppt

