Bài giảng Đại số Lớp 12 - Tiết 16: Ôn tập chương 1
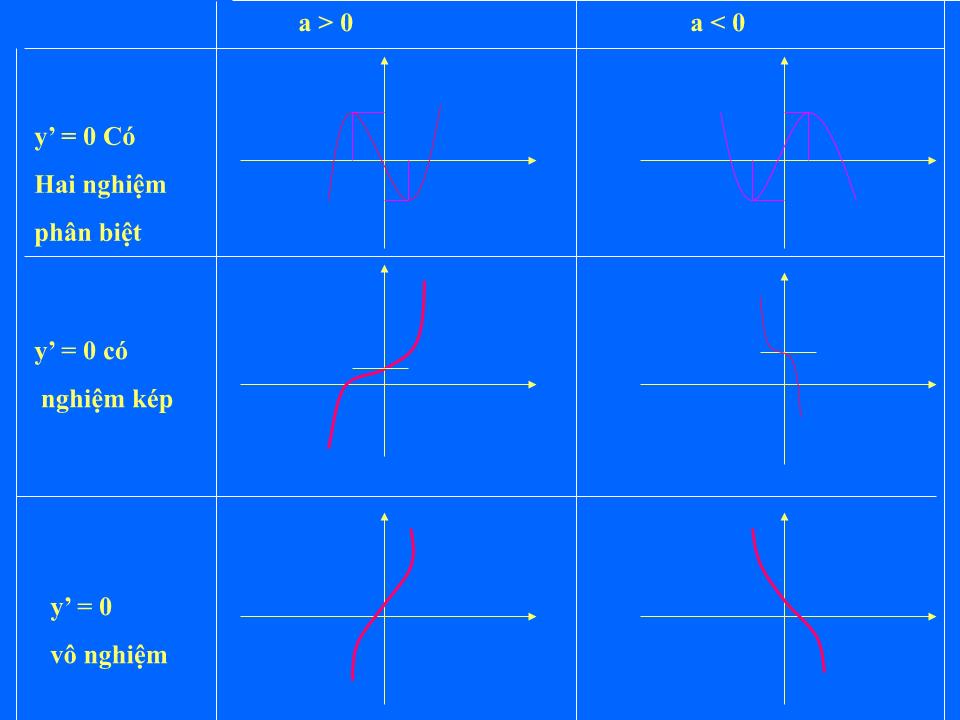
1) Khi nào thì hàm số luôn đồng biến trên R ?
2) Khi nào thì hàm số luôn nghịch biến trên R ?
3) Khi nào hàm số có CĐ, CT?
4) Khi nào hàm số không có CĐ, CT?
2. Cho hàm số:
a) Chứng tỏ rằng với mọi m, hàm số luôn có cực đại, cực tiểu.
b) Tìm m để hàm số đạt cực tiểu tại x = 2. Khảo sát và vẽ đồ thị của hàm số với m vừa tìm được.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
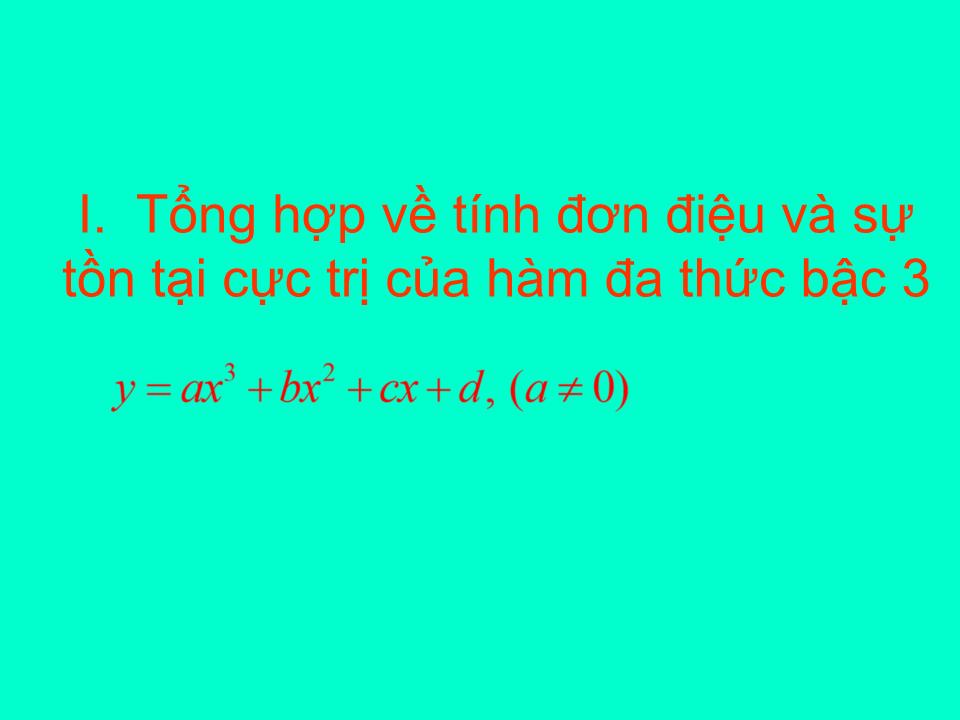
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Tiết 16: Ôn tập chương 1", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Tiết 16: Ôn tập chương 1

Câu hỏi 1: Phát biểu các điều kiện để hàm số đồng biến, nghịch biến? Kiểm tra bài cũ: + f(x) đồng biến trên khoảng K ↔ f’(x)≥0, + f(x) nghịch biến trên khoảng K ↔ f’(x)≥0, Trả lời c âu hỏi 1 : (f’(x)=0 tại hữu hạn điểm trên K) Câu hỏi 2: Nêu điều kiện đủ để hàm số có cực trị ? 2. Điều kiện đủ để hàm số có cực trị: Dấu hiệu 1: * f’(x) đổi dấu từ (+) sang (-) tại điểm x 0 thì x 0 là điểm cực đại. * f’(x) đổi dấu từ (-) sang (+) tại điểm x 0 thì x 0 là điểm cực tiểu. Dấu hiệu 2: * x 0 là điểm cực đại * x 0 là điểm cực tiểu tiết 16: ôn tập chương I I. Tổng hợp về tính đơn điệu và sự tồn tại cực trị của hàm đa thức bậc 3 y’ = 0 Có Hai nghiệm phân biệt y’ = 0 có nghiệm kép y’ = 0 vô nghiệm a > 0 a < 0 1) Khi nào thì hàm số luôn đồng biến trên R ? 2) Khi nào thì hàm số luôn nghịch biến trên R ? 3) Khi nào hàm số có CĐ, CT? 4) Khi nào hàm số không có CĐ, CT? *Xét hàm số: * Hàm số đồng biến trên R * Hàm số nghịch biến trên R * Hàm số có cực trị * Hàm số không có cực trị Bài tập: 1. Bài 8 (SGK – 46) TXĐ: D=R Hàm số đồng biến trên R khi b) Để hàm số có cực đại và cực tiểu thì y' = 0 có 2 nghiệm phân biệt 2. Cho hàm số: a) Chứng tỏ rằng với mọi m, hàm số luôn có cực đại, cực tiểu. b) Tìm m để hàm số đạt cực tiểu tại x = 2. Khảo sát và vẽ đồ thị của hàm số với m vừa tìm được. Giải: TXĐ: D=R Vậy với mọi m, y’ luôn có hai nghiệm phân biệt nên hàm số có CĐ, CT với mọi m b) Với mọi m y’ có 2 nghiệm phân biệt x 1 =m-1, x 2 =m+1 Ta có bảng xét dấu của y’: Suy ra hàm số đạt cực tiểu tại x=m+1 Bài ra hàm số đạt cực tiểu tại x=2, ta có: m + 1 = 2 m=1 Vậy để hàm số đạt cực tiểu tại x=2 thì m = 1. Với m = 1, ta có hàm số: * ĐỒ THỊ: II. Tổng hợp về tính đơn điệu và sự tồn tại cực trị của hàm trùng phương TXĐ: D = R. Suy ra: Nếu a.b>0 hoặc b=0 thì hàm số chỉ có một cực trị - Nếu a.b<0 thì hàm số có 3 cực trị. 3. Tìm m để hàm số sau có đúng 1 cực trị: Giải TXĐ: D=R Hàm số có đúng một cực trị y’ có một nghiệm duy nhất m 0 Vậy với m 0 thì hàm số có đúng một cực trị Củng cố bài học: Qua bài học các em cần nắm vững: Điều kiện hàm số bậc 3 luôn đồng biến trên R. 2) Điều kiện hàm số bậc 3 luôn nghịch biến trên R. 3) Điều kiện hàm số bậc 3 có CĐ, CT. 4) Điều kiện hàm số bậc 3 không có CĐ, CT. 5) Điều kiện để hàm trùng phương có 1 (hoặc 3) cực trị. Bài tập về nhà: 1. Bài 8 (SGK - 44) 2. Bài 10 (SGK – 46) 3. Các bài trong sách bài tập: 1. 29; 1.31; 1.33; 1.34 Bài tập trắc nghiệm: 1. Số điểm cực trị của hàm số: A. 3 B. 1 C. 2 D. 0 2. Hàm số Đồng biến trên khoảng: A. B. C. D. 3. Số điểm cực trị của hàm số: A. 0 B. 1 C. 2 D. 3 4. Số điểm cực trị của hàm số: A. 0 B. 1 C. 2 D. 3 Đáp án: C Đáp án: D Đáp án: B Đáp án: A * Điều kiện để hàm số luôn đồng biến (nghịch biến) trên TXĐ của nó ? +f(x) đồng biến trên D ↔f’(x)≥0, +f(x) nghịch biến trên D ↔f’(x)≥0, (f’(x)=0 t ại hữu hạn điểm trên D) Câu hỏi 2: Nêu cách tìm cực đại, cực tiểu của hàm số nhờ xét dấu đạo hàm f’(x)? + Tìm TXĐ, tính f’(x). + Tìm điểm tại đó f’(x)=0 hoặc f’(x) không xác định. + Lập bảng xét dấu f’(x). + KL: (Dựa vào dấu hiệu tồn tại cực trị để kết luận).
File đính kèm:
 bai_giang_dai_so_lop_12_tiet_16_on_tap_chuong_1.ppt
bai_giang_dai_so_lop_12_tiet_16_on_tap_chuong_1.ppt

