Bài giảng Đại số Lớp 12 - Ôn tập chương 3 - Cao Lam Sơn

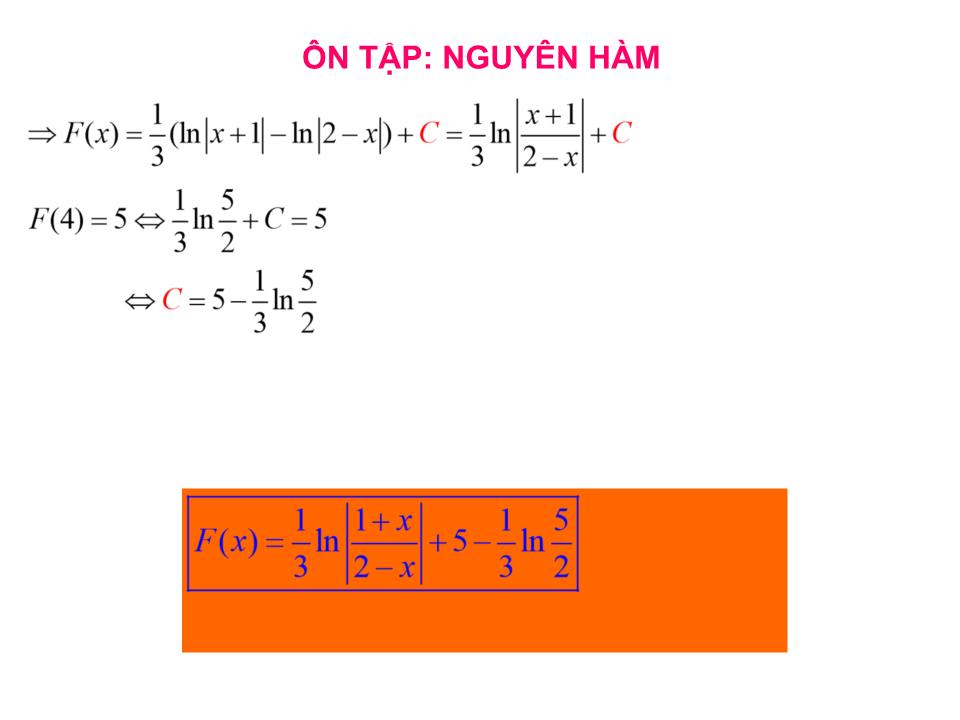
GV THỰC HIỆN : CAO LAM SƠN 
 ÔN TẬP CHƯƠNG III 
ÔN TẬP CHƯƠNG III 
1) Nguyên hàm 
2) Tích phân 
3) Ứng dụng tích phân trong hình học 
I. Lý thuyết : 
Nguyên hàm HS sơ cấp 
Nguyên hàm HS hợp 
Bài 1: Tìm nguyên hàm các hàm số sau : 
ÔN TẬP: NGUYÊN HÀM 
Đáp án 
ÔN TẬP: NGUYÊN HÀM 
Đặt 
ÔN TẬP: NGUYÊN HÀM 
Đặt 
ÔN TẬP: NGUYÊN HÀM 
Bài 2: Tìm một nguyên hàm F(x ) của 
. 
biết F(4)=5 
ÔN TẬP: NGUYÊN HÀM 
ÔN TẬP: NGUYÊN HÀM 
ÔN TẬP: TÍCH PHÂN 
1.Phương pháp đổi biến số 
Đổi biến số dạng 1: Đặt x = u(t). Có 2 loại: 
Loại 1: Với các tích phân có dạng hoặc 
thì ta đặt 
Loại 2: Với các tích phân có dạng hoặc 
thì ta đặt hoặc 
Chú ý: Phương pháp đổi biến số dạng dạng 1 ngoài dùng để tính các tích phân thuộc 2 loại trên còn được dùng trong các bài toán biến đổi tích phân. 
ÔN TẬP: TÍCH PHÂN 
1.Phương pháp đổi biến số 
Ví dụ: 
2. Nếu f(x) là hàm số chẵn và liên tục trên đoạn [-a ; a], a > 0 thì: 
3. Nếu f(x) là hàm số lẻ và liên tục trên đoạn [-a ; a], a > 0 thì: 
Đổi biến số dạng 1: Đặt x = u(t). 
ÔN TẬP: TÍCH PHÂN 
1.Phương pháp đổi biến số 
Ví dụ: 
4. Nếu f(x) là hàm số chẵn và liên tục trên đoạn [-a ; a], a > 0 thì: 
Đổi biến số dạng 1: Đặt x = u(t). 
5. Nếu f(x) là hàm số liên tục trên đoạn [-a ; a], a > 0 thì: 
ÔN TẬP: TÍCH PHÂN 
1.Phương pháp đổi biến số 
Đổi biến số dạng 2: Tích phân dạng: Đặt t = u ( x ) 
Nhận xét: - Trong thực hành, ta có thể trình bày một cách thuận tiện phép đổi biến số này mà không cần đưa ra biến t . 
Ví dụ: 
ÔN TẬP: TÍCH PHÂN 
1.Phương pháp đổi biến số 
Đổi biến số dạng 2: Tích phân dạng: Đặt t = u ( x ) 
Nhận xét: - Trong thực hành, ta có thể trình bày một cách thuận tiện phép đổi biến số này mà không cần đưa ra biến t . 
Chú ý: - Nhiều khi ta phải biến đổi trước khi thực hiện phép đổi biến số. 
Ví dụ: 
ÔN TẬP: TÍCH PHÂN 
2.Phương pháp tích phân từng phần 
Trong thực hành ta thường gặp các dạng tích phân sau: 
Cách giải: 
với P(x) là đa thức. 
Dạng 1: 
Dạng 2: 
Cách giải: 
Dạng 3: 
Cách giải: 
Tích phân hồi quy. 
Đặt u = P(x), dv = sinxdx (hoặc dv = cosxdx, dv = e x dx). 
Đặt u = lnx, dv = f(x)dx. 
Đặt u = e x , dv = sinxdx (hoặc dv = cosxdx). Tích phân từng phần 2 lần. 
ÔN TẬP: TÍCH PHÂN 
2.Phương pháp tích phân từng phần 
Ngoài ra ta còn gặp một số dạng tích phân sau: 
Dạng 4: 
Cách giải: Đặt u = sin(lnx) (u = cos(lnx)), dv = dx. Tích phân từng phần 2 lần. 
Tích phân hồi quy. 
Chú ý: - Có những bài toán phải tính tích phân từng phần nhiều lần. 
- Đối với dạng 1: Số lần tích phân từng phần bằng số bậc của đa thức P(x). 
- Đối với dạng 2: Số lần tích phân từng phần bằng số bậc của hàm số y = lnx. 
Bài 3: Tính các tích phân sau : 
ÔN TẬP: TÍCH PHÂN 
Đáp án : 
a) 8/3 
ÔN TẬP: TÍCH PHÂN 
Giải : 
ÔN TẬP: TÍCH PHÂN 
Bài 4: Tính tích phân sau : 
Đặt 
ÔN TẬP: TÍCH PHÂN 
3. B ài tập 
Tính các tích phân sau: 
ÔN TẬP: TÍCH PHÂN 
4. CỦNG CỐ 
- Chú ý rèn luyện kĩ năng nhận dạng và vận dụng để tính tính phân. 
- Đối với tích phân đổi biến khi tính toán cần chú ý điều gì? 
- Đối với tích phân từng phần khi tính toán cần chú ý điều gì? 
5. DẶN DÒ 
- Về nhà xem và làm lại các bài tập trong SGK và sách bài tập. 
- Ôn lại phần diện tích và thể tích, làm các bài tập trong SBT. 
CHÀO THÂN ÁI-HẸN GẶP LẠI