Bài giảng Đại số Lớp 12 - Ôn tập chương 2 - Vũ Chí Cương
CẦN NẮM NHỮNG VẤN ĐỀ CƠ BẢN CỦA CHƯƠNG
Tính chất luỹ thừa với số mũ thực
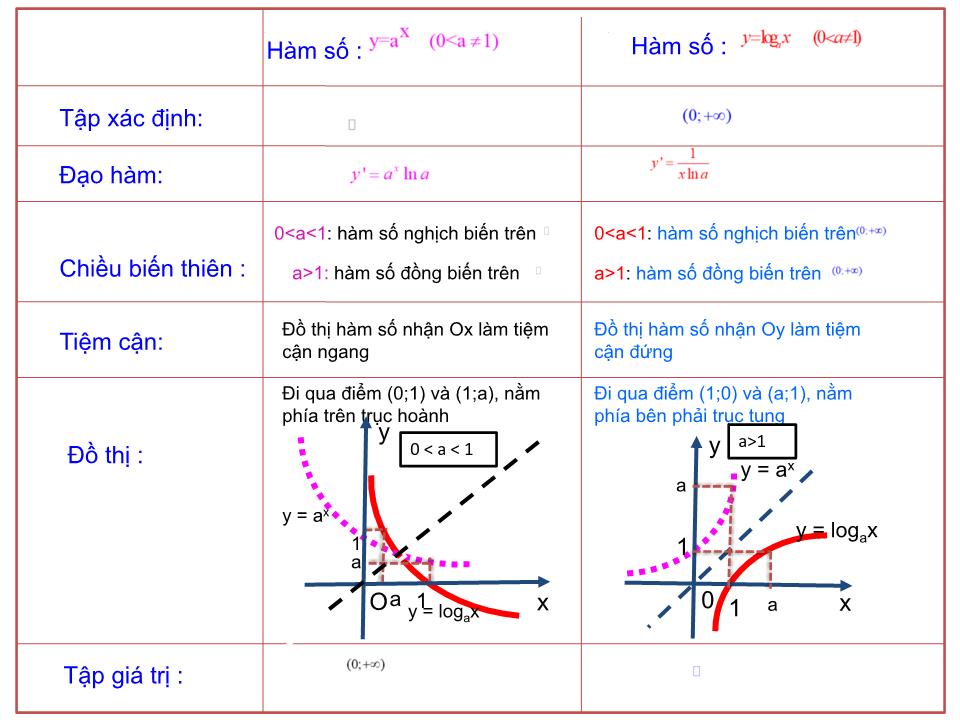
Tính chất của hàm số luỹ thừa, hàm số mũ, hàm số lôgarit
Các công thức tính đạo hàm của hàm số lũy thừa, mũ, hàm số lôgarit
Các quy tắc tính lôgarit
Cho các số thực dương a,b,c,x,y và a,c khác 1,ta có

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Ôn tập chương 2 - Vũ Chí Cương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Ôn tập chương 2 - Vũ Chí Cương

NHIỆT LIỆT CHÀO MỪNG CÁC THẦY CÔ VÀ CÁC EM HỌC SINH VỀ DỰ HỘI GIẢNG! Gv: Vũ Chí C ươ ng Bộ môn : giải tích 12 Tính đạo hàm của hàm số: KIỂM TRA BÀI CŨ TRƯỜNG THPT CHI LINH Đồ thị : Hàm số : Hàm số : Tập xác định: Đạo hàm: Chiều biến thiên : Tiệm cận: Tập giá trị : 0<a<1 : hàm số nghịch biến trên a>1: hàm số đồng biến trên 0<a<1 : hàm số nghịch biến trên a>1 : hàm số đồng biến trên Đồ thị hàm số nhận Ox làm tiệm cận ngang Đồ thị hàm số nhận Oy làm tiệm cận đứng Đi qua điểm (0;1) và (1;a), nằm phía trên trục hoành Đi qua điểm (1;0) và (a;1), nằm phía bên phải trục tung y = log a x y = a x y = a x y = log a x 0 < a < 1 a 1 y 1 x O a x 0 1 1 a a y a>1 Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 1: Tính giá trị biểu thức , biết , biết Bài 2: Giải các phương trình sau Bài 3: Giải các bất phương trình sau Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II CẦN NẮM NHỮNG VẤN ĐỀ CƠ BẢN CỦA CHƯƠNG - Tính chất luỹ thừa với số mũ thực - Tính chất của hàm số luỹ thừa, hàm số mũ, hàm số lôgarit Một số cách giải các các phương trình, bất phương trình mũ và lôgarit. - Đưa về cùng cơ số Đặt ẩn phụ Lôgarit hoá ( mũ hoá) - Các công thức tính đạo hàm của hàm số lũy thừa, mũ, hàm số lôgarit H Ư ỚNG DẪN HỌC Ở NHÀ Xem lại các bài tập đã làm, làm các bài tập còn lại, làm bài tập: 2.40_Sbt(108), 2.45_Sbt(109),2.46-2.50_Sbt(109) Ôn tập chuẩn bị kiểm tra 45 phút - Các quy tắc tính lôgarit Cho a>0,b>0 ta có Bảng tính chất luỹ thừa với số mũ thực (trang 54 SGK) Nếu a>1 thì Nếu 0<a<1 thì Đạo hàm của hàm sơ cấp Đạo hàm của hàm hợp (u=u(x) Các công thức tính đạo hàm của hàm số luỹ thừa, mũ, lôgarit(Trang 77) Cho các số thực dương a,b,c,x,y và a,c khác 1,ta có Các quy tắc tính lôgarit Chân thành cảm ơn! Chúc các em học tập đạt kết quả cao! Chân thành cảm ơn! Chúc các em học tập đạt kết quả cao! Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 1: Tính giá trị biểu thức Có Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II , biết Bài 1: Tính giá trị biểu thức Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 2: Giải các phương trình sau TXĐ:D=(0;+ ) Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 2: Giải các phương trình sau Đặt Kết hợp với t>0 được t=4/3 Với t=4/3 Giải (điều kiện t>0) ta có Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 2: Giải các phương trình sau đkxđ Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 3: Giải các bất phương trình sau Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Bài 3: Giải các bất phương trình sau đkxđ Giải Thø 7 ngµy 12 th¸ng 11 năm 2011 ÔN TẬP CHƯƠNG II Nếu a>1 thì Bảng tính chất luỹ thừa với số mũ thực Cho a>0,b>0 ta có Nếu 0<a<1 thì y = log a x y = a x 0 < a < 1 a 1 y 1 x O a y = a x y = log a x x 0 1 1 a a y a>1 Cho các số thực dương a,b,c,x,y và a,c khác 1,ta có Các quy tắc tính lôgarit Các công thức tính đạo hàm của hàm số luỹ thừa, mũ, lôgarit Đạo hàm của hàm sơ cấp Đạo hàm của hàm hợp (u=u(x) Các công thức tính đạo hàm của hàm số luỹ thừa, mũ, lôgarit(Trang 77) Đạo hàm của hàm sơ cấp Đạo hàm của hàm hợp (u=u(x) Các quy tắc tính lôgarit Cho các số thực dương a,b,c,x,y và a,c khác 1,ta có Nếu a>1 thì Nếu 0<a<1 thì Cho a>0,b>0 ta có Bảng tính chất luỹ thừa với số mũ thực (trang 54 SGK) Nếu a>1 thì Nếu 0<a<1 thì Nếu a>1 thì Bảng tính chất luỹ thừa với số mũ thực (trang 54 SGK) Cho a>0,b>0 ta có Nếu 0<a<1 thì Bảng tính chất luỹ thừa với số mũ thực (trang 54 SGK)
File đính kèm:
 bai_giang_dai_so_lop_12_on_tap_chuong_2_vu_chi_cuong.ppt
bai_giang_dai_so_lop_12_on_tap_chuong_2_vu_chi_cuong.ppt

