Bài giảng Đại số Lớp 12 - Chương 4: Số phức - Bài 1: Số phức - Cao Thị Diệu Phước

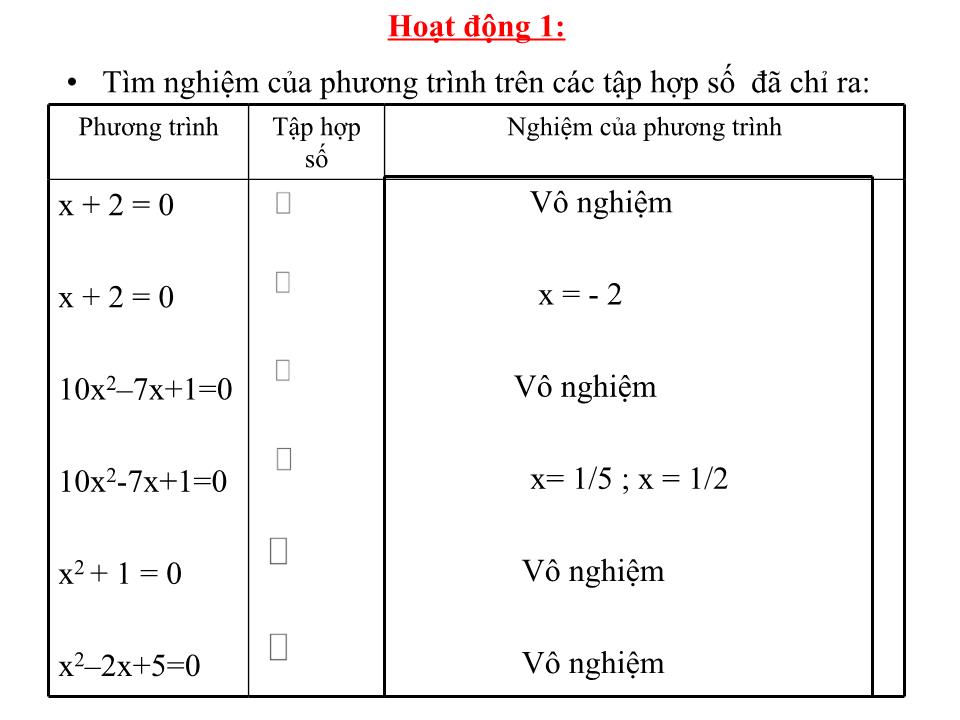
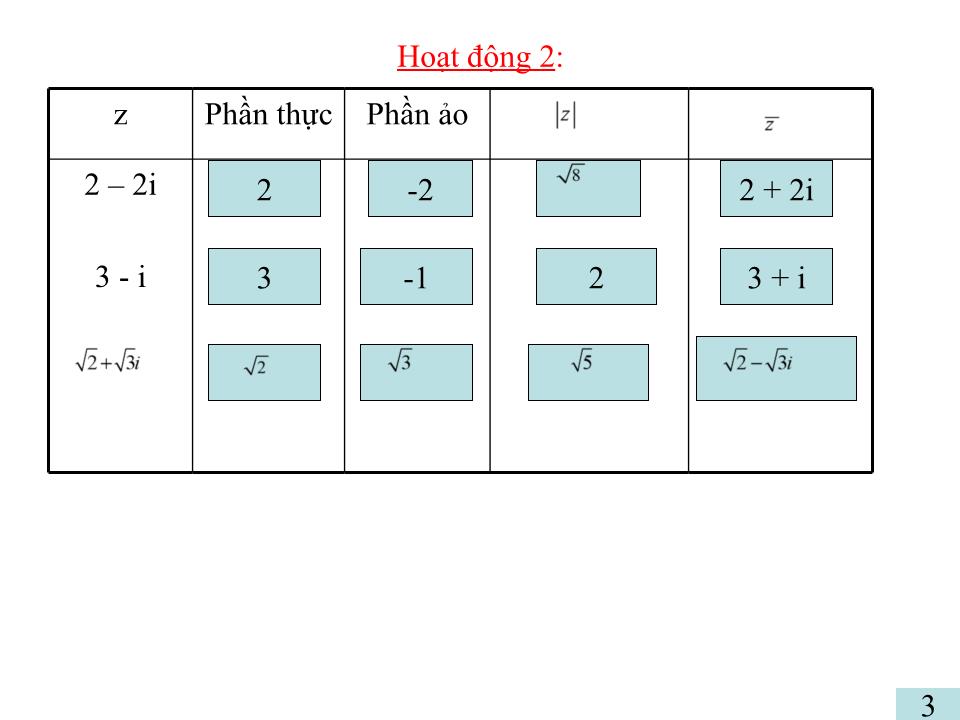
Bài 1 : Số Phức 
Lớp : 12A1 
GV : Cao Thị Diệu Phước 
Chào Mừng Quý Thầy Cô Tham Dự Thao Giảng 
Hoạt động 1: 
Tìm nghiệm của phương trình trên các tập hợp số đã chỉ ra: 
Phương trình 
Tập hợp số 
Nghiệm của phương trình 
x + 2 = 0 
x + 2 = 0 
10x 2 –7x+1=0 
10x 2 -7x+1=0 
x 2 + 1 = 0 
x 2 –2x+5=0 
 Vô nghiệm 
 x = - 2 
 Vô nghiệm 
 x= 1/5 ; x = 1/2 
 Vô nghiệm 
 Vô nghiệm 
Chương IV : Số Phức Bài 1 : Số Phức 
Số i : 
 i gọi là đơn vị ảo 
2. Định nghĩa số phức : 
 Số phức là một biểu thức có dạng : z = a + bi (a; b ; i 2 = -1) 
 Trong đó : a là phần thực 
 b là phần ảo 
 *Tập hợp các số phức kí hiệu là 
i 2 = -1 
VD1 : Tìm phần thực và phần ảo của các số phức sau : 
5 - 6i b. -5 + 4i c. 7 d. 
Chú ý : 
 1. a = a + 0i là một số phức ( ) 
 Ta có : 
 2. Số phức 0 + bi = bi gọi là số thuần ảo. 
3. Số phức bằng nhau 
VD2 : Tìm các số thực x; y để 2 số phức z 1 ; z 2 bằng nhau: 
 1. z 1 = x - 2y + (y + x) i; z 2 = -2 + i. 
 2. z 1 = x + y + (2 – 3x)i; z 2 = 4 - 2y + (2 – 3y)i. 
Giải : 
 1. Vì z 1 = z 2 nên x; y là nghiệm của hệ: 
 2. Vì z 1 = z 2 nên x; y là nghiệm của hệ: 
a + bi = c + di 
4 
4. Biểu diễn hình học số phức : 
 Điểm M(a; b) trong hệ tọa độ vuông góc Oxy gọi là điểm biểu diễn của số phức z = a + bi 
 - Mặt phẳng Oxy gọi là mặt phẳng phức 
 - Ox là trục thực 
 - Oy là trục ảo 
VD3 : Hãy biểu diễn các số phức sau trên mặt phẳng tọa độ: 
 z 1 = 3 + 2i; z 2 = -3 - 2i 
O 
x 
y 
a 
b 
M 
5 
5. Môđun của số phức : 
 M(a; b) là điểm biểu diễn của số phức z = a + bi 
 Độ dài vectơ gọi là mô đun của số phức z. 
 Kí hiệu: 
O 
x 
y 
a 
b 
M 
6 
6. Số phức liên hợp : 
 Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hiệp của z. 
 Kí hiệu: 
 Nhận xét : 
 a. Các điểm biểu diễn z và đối xứng nhau qua trục Ox. 
 b. 
 c. 
O 
x 
y 
a 
b 
-b 
M 
M’ 
Hoạt động 2 : 
z 
Phần thực 
Phần ảo 
2 – 2i 
3 - i 
2 
-2 
2 + 2i 
3 
3 + i 
-1 
2 
3