Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Tiết 60: Ứng dụng tích phân để tính diện tích hình phẳng
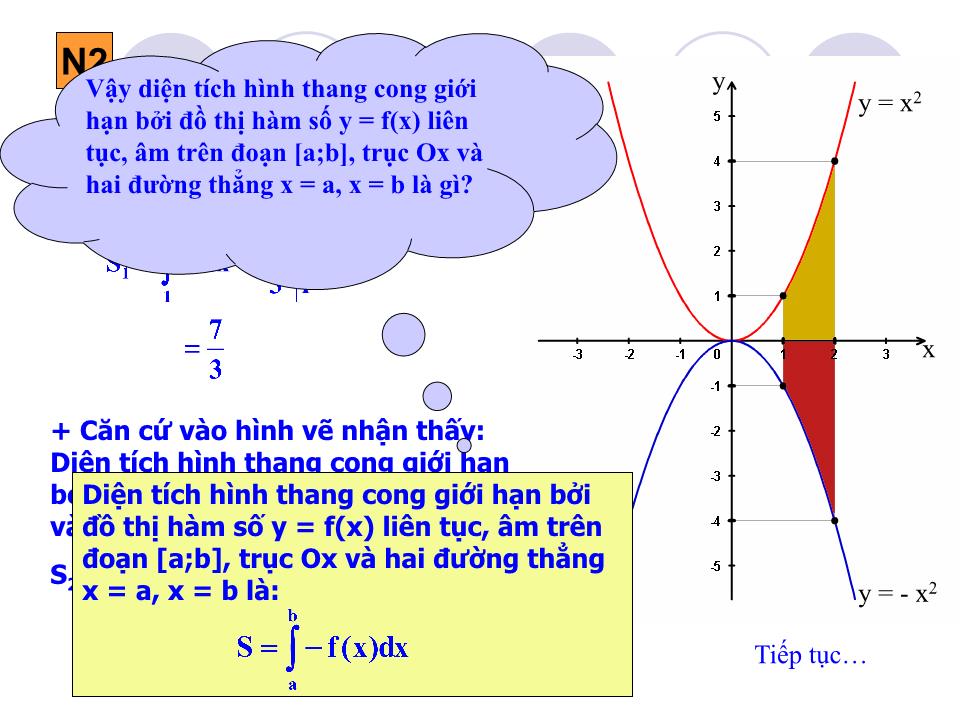
Vậy diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) liên tục, âm trên đoạn [a;b], trục Ox và hai đường thẳng x = a, x = b là gì?
Căn cứ vào hình vẽ nhận thấy: Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = - x2, trục Ox và hai đường thẳng x = 1, x = 2 là:
S2 = S1 =
Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) liên tục, âm trên đoạn [a;b], trục Ox và hai đường thẳng x = a, x = b là:
Ta thực hiện như sau:
Giải phương trình f(x) – g(x) = 0 trên đoạn [a; b], giả sử pt có các nghiệm c, d (a ≤ c < d ≤ b).
Trên từng đoạn [a;c], [c;d], [d;b] thì f(x) – g(x) không đổi dấu.
Trên mỗi đoạn đó, chẳng hạn trên đoạn [c; d], ta có

Trang 1
Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Tiết 60: Ứng dụng tích phân để tính diện tích hình phẳng

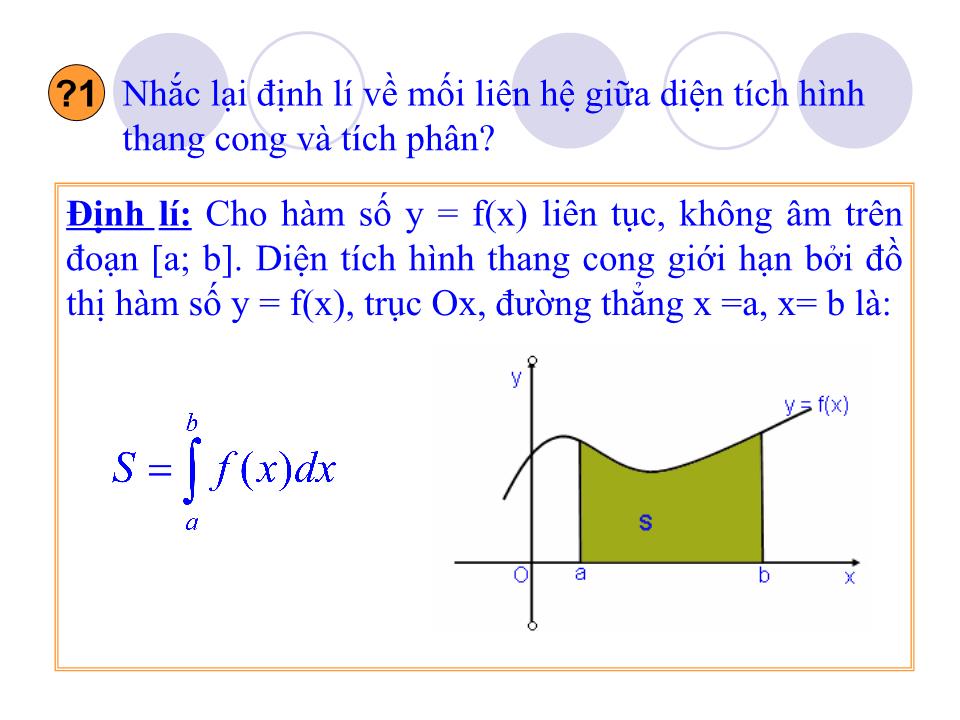
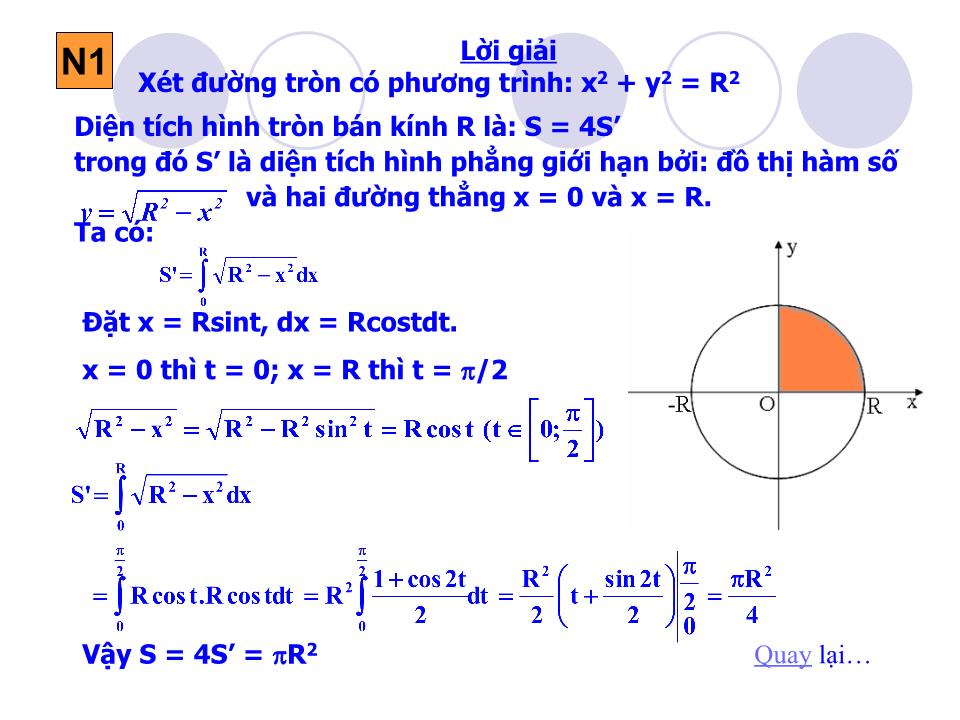
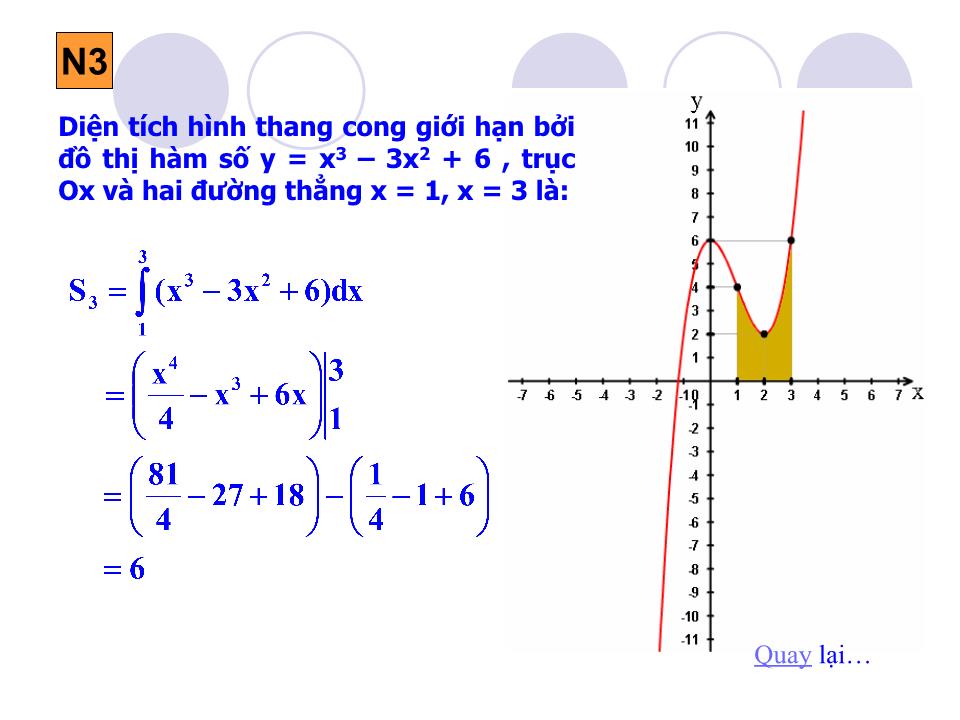
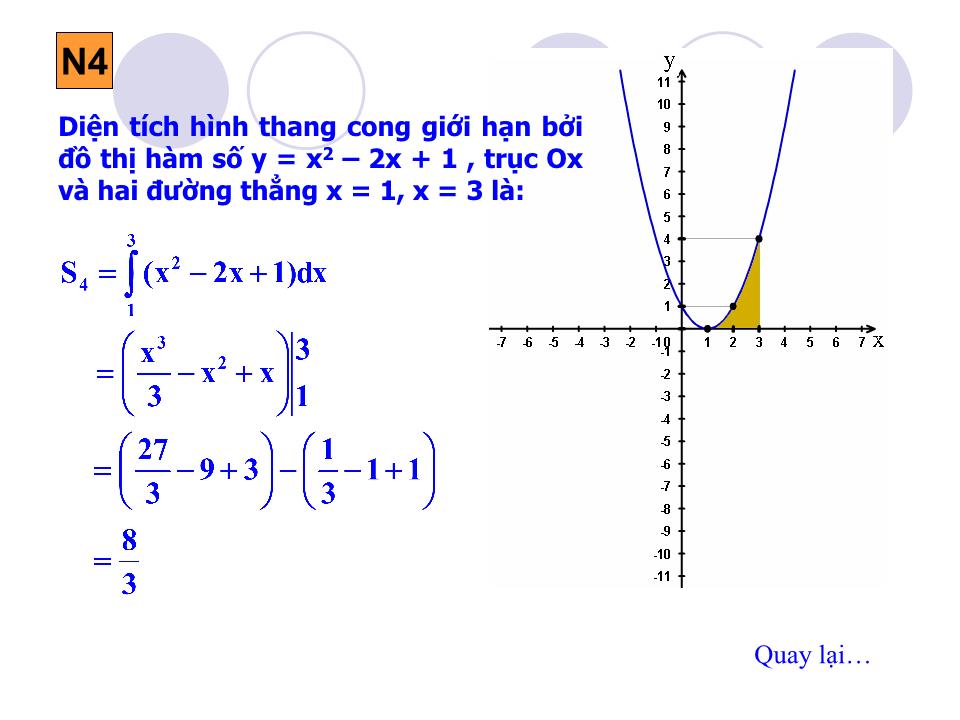
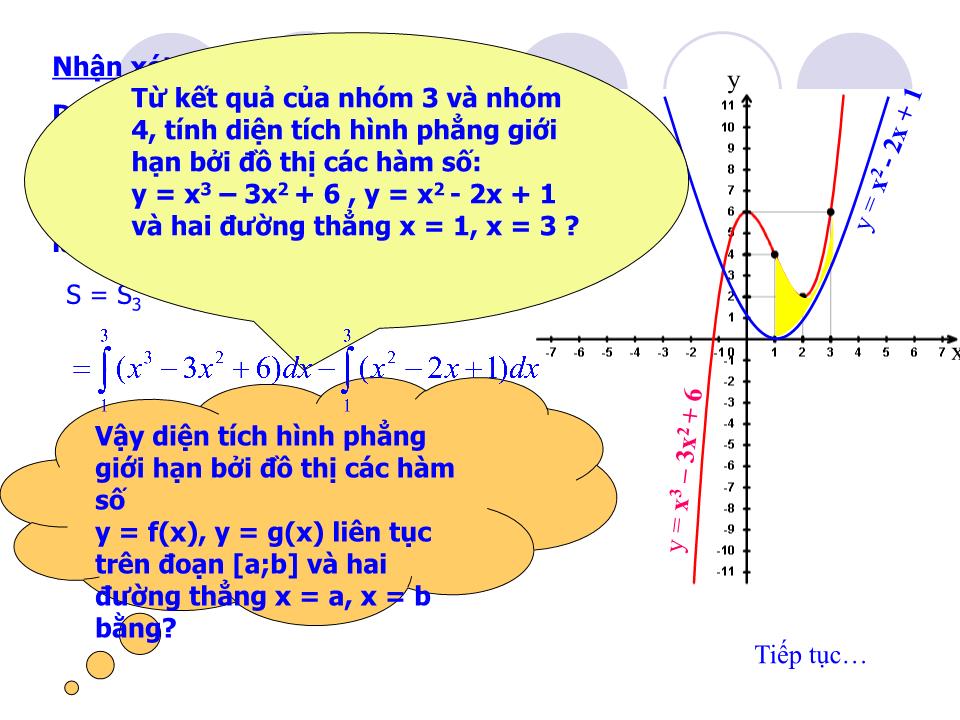
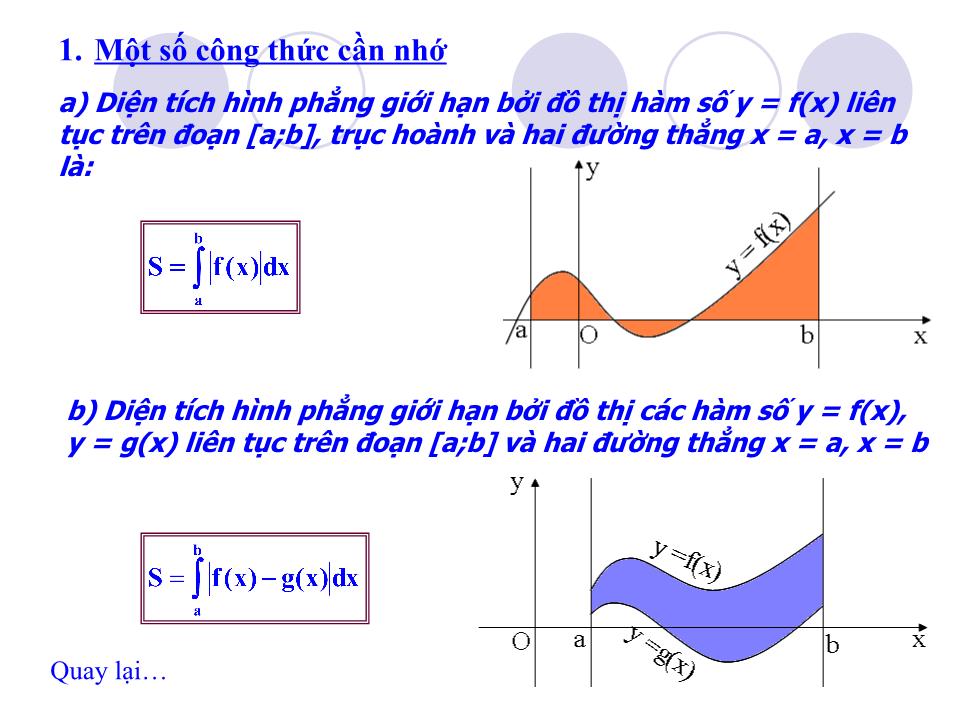
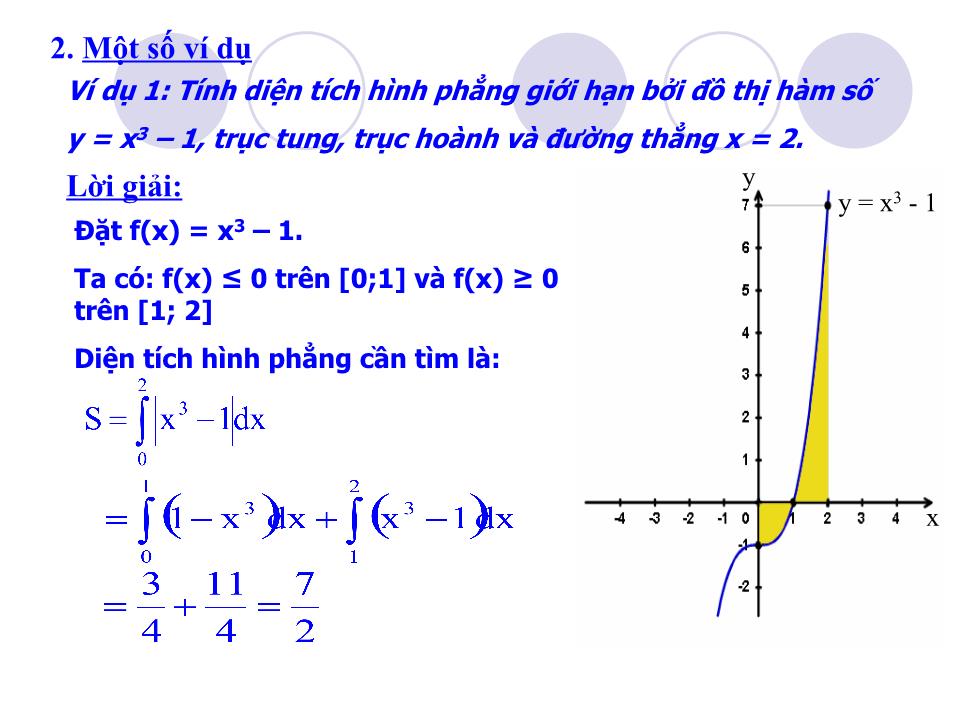
Tiết 60 Ứ NG DỤNG TÍCH PHÂN ĐỂ TÍNH DIỆN TÍCH HÌNH PHẲNG Nhắc lại định lí về mối liên hệ giữa diện tích hình thang cong và tích phân? Định lí: Cho hàm số y = f(x) liên tục, không âm trên đoạn [a; b]. Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox, đ ư ờng thẳng x =a, x= b là: ?1 Nhóm 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 – 2x + 1, trục hoành và hai đ ư ờng thẳng x = 1, x = 3. Nhóm 1: Tính diện tích hình tròn bán kính R giới hạn bởi đ ư ờng tròn có ph ươ ng trình : x 2 + y 2 = R 2 Nhóm 2: + Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x 2 , trục hoành và hai đ ư ờng thẳng x = 1, x = 2. + Vẽ đồ thị hàm số y = - x 2 từ đó so sánh diện tích hình thang cong giới hạn bởi đồ thị hàm số y = - x 2 trục hoành và hai đ ư ờng thẳng x = 1, x = 2 v ớ i kết quả ở trờn . Nhóm 3: Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x 3 – 3x 2 + 6, trục hoành và hai đ ư ờng thẳng x = 1, x = 3. H1 Thực hiện các bài tập sau: Diện tích hình tròn bán kính R là: S = 4S’ trong đó S’ là diện tích hình phẳng giới hạn bởi: đồ thị hàm số và hai đường thẳng x = 0 và x = R. Ta có: Đặt x = Rsint, dx = Rcostdt. x = 0 thì t = 0; x = R thì t = /2 Vậy S = 4S’ = R 2 N1 Quay lại Lời giải Xét đường tròn có phương trình: x 2 + y 2 = R 2 x y N2 + Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x 2 , trục Ox và hai đường thẳng x = 1, x = 2 là: + Căn cứ vào hình vẽ nhận thấy: Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = - x 2 , trục Ox và hai đường thẳng x = 1, x = 2 là: S 2 = S 1 = y = x 2 y = - x 2 Vậy diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) liên tục, âm trên đoạn [a;b], trục Ox và hai đường thẳng x = a, x = b là gì? Tiếp tục Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) liên tục, âm trên đoạn [a;b], trục Ox và hai đường thẳng x = a, x = b là: Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x 3 – 3x 2 + 6 , trục Ox và hai đường thẳng x = 1, x = 3 là: N3 Quay lại N4 Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x 2 – 2x + 1 , trục Ox và hai đường thẳng x = 1, x = 3 là: Quay lại x y Nhận xét: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số: y = x 3 – 3x 2 + 6 , y = x 2 - 2x + 1 và hai đường thẳng x = 1, x = 3 là: S = S 3 – S 4 Vậy diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b] và hai đường thẳng x = a, x = b bằng? Tiếp tục Từ kết quả của nhóm 3 và nhóm 4, tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số: y = x 3 – 3x 2 + 6 , y = x 2 - 2x + 1 và hai đường thẳng x = 1, x = 3 ? y = x 3 – 3x 2 + 6 y = x 2 - 2x + 1 Một số công thức cần nhớ a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x = a, x = b là: b) Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b] và hai đường thẳng x = a, x = b Quay lại 2. Một số ví dụ Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 3 – 1, trục tung, trục hoành và đường thẳng x = 2. Lời giải: Đặt f(x) = x 3 – 1. Ta có: f(x) ≤ 0 tr ên [0;1] và f(x) ≥ 0 tr ên [1; 2] Diện tích hình phẳng cần tìm là: y x y = x 3 - 1 Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số: f 1 (x) = x 3 – 3x và f 2 (x) = x Lời giải: Phương trình hoành độ giao điểm của đồ thị hai hàm số f 1 (x) = x 3 – 3x và f 2 (x) = x là: Diện tích hình phẳng cần tìm là: x y f 1 (x) =x 3 – 3x f 2 (x) =x 3. Bài tập vận dụng Thực hiện H1 và H2 trong sách giáo khoa! H1 : Tìm diện tích hình phẳng giới hạn bởi đồ thị hàm số: y = 4 – x 2 , đường thẳng x = 3, trục tung và trục hoành. H2 : Tính diện tích hình phẳng giới hạn bởi đường thẳng y = x + 2 và Parabol y = x 2 + x - 2 H1 : Giải : Đặt f(x) = 4 – x 2 , f(x) ≥ 0 tr ên [0; 2] và f(x) ≤ 0 tr ên [2; 3] nên: H2 : Giải : PT hoành độ giao điểm: x 2 + x - 2 = x + 2 x = -2; x = 2. Vậy: Chú ý: + Để khử dấu giá trị tuyệt đối trong công thức: • Giải phương trình f(x) – g(x) = 0 trên đoạn [a; b], giả sử pt có các nghiệm c, d (a ≤ c < d ≤ b). Trên từng đoạn [a;c], [c;d], [d;b] thì f(x) – g(x) không đổi dấu. Trên mỗi đoạn đó, chẳng hạn trên đoạn [c; d], ta có: Ta thực hiện như sau: Củng cố: - Ghi nhớ các công thức tính diện tích hình phẳng. - Bài tập đề nghị: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số: y = x 2 – 4x +3, y = - 2x + 2 và y = 2x – 6. y = x 2 - 4x + 3 y = -2x + 2 y = 2x - 6 y x
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_3_nguyen_ham_tiet_60_ung_dung.ppt
bai_giang_dai_so_lop_12_chuong_3_nguyen_ham_tiet_60_ung_dung.ppt

