Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Bài 2: Tích phân (Tiết 1) - Lưu Công Hoàn
Cho hàm số y = f(x) liên tục, không đổi dấu
trên đoạn [a;b]. Hình phẳng giới hạn bởi:
Đồ thị hàm số y = f(x), trục Ox, và hai đường thẳng x = a; x = b được gọi là hình thang cong
Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a;b] thì ta có thể chứng minh được rằng diện tích của hình thang cong là:
S = F(b) – F(a)
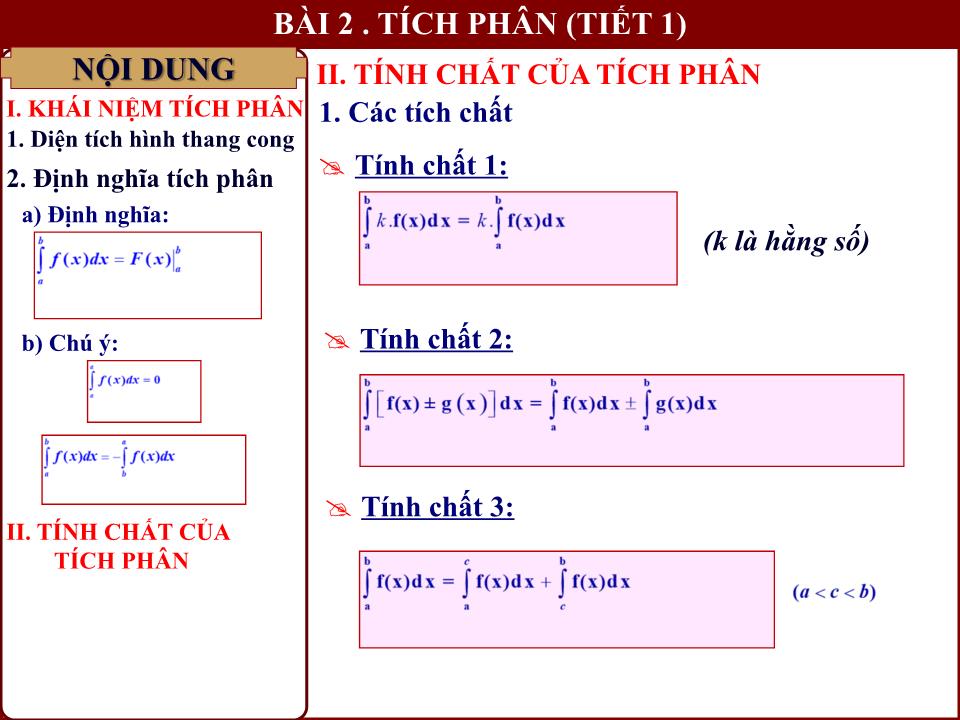
Định nghĩa:
Cho f(x) là hàm số liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của f(x) trên đọan [a;b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay gọi là tích phân xác định trên đoạn [a;b] của hàm số f(x)).

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Bài 2: Tích phân (Tiết 1) - Lưu Công Hoàn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Bài 2: Tích phân (Tiết 1) - Lưu Công Hoàn

Chào mừng các thầy, cô tới dự giờ th ă m lớp! Giáo viên : L Ư U CÔNG HOÀN ?1 Chứng tỏ rằng: F(x) = x 3 - x 2 +1 và G(x) = x 3 - x 2 - 1 đều là nguyên hàm của hàm số f(x) = 3x 2 - 2x KIỂM TRA BÀI CŨ ?2 Chứng tỏ rằng: F(2) – F(1) = G(2) – G(1) H ƯỚNG DẪN ?1 Dễ thấy: F’(x) = G’(x) = 3x 2 - 2x = f(x) => đ pcm ?2 Tính được F(2) – F(1) = 4 = G(2) – G(1) Bài 2. Tích Phân (Tiết 1) TIẾT 54 NỘI DUNG BÀI DẠY KHÁI NIỆM TÍCH PHÂN CÁC TÍNH CHẤT CỦA TÍCH PHÂN III. PH ƯƠ NG PHÁP TÍNH TÍCH PHÂN CH ƯƠ NG III. NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG BÀI 2 . TÍCH PHÂN (TIẾT 1) y = f(x) a b O y x I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG I. KHÁI NIỆM TÍCH PHÂN 1. Diện tích hình thang cong Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a;b]. Hình phẳng giới hạn bởi: Đồ thị hàm số y = f(x), trục Ox, và hai đường thẳng x = a; x = b được gọi là hình thang cong 1. Diện tích hình thang cong Giả sử F(x) là một nguyên hàm của f(x) trên đ oạn [ a;b ] thì ta có thể chứng minh được rằng diện tích của hình thang cong là: S = F(b) – F(a) BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân S = F(b) – F(a) F(x) là một nguyên hàm của f(x) trên đ oạn [ a;b ] I. KHÁI NIỆM TÍCH PHÂN 2. Định nghĩa tích phân Cho f(x) là hàm số liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của f(x) trên đọan [a;b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay gọi là tích phân xác định trên đoạn [a;b] của hàm số f(x)) . Kí hiệu là: a) Định nghĩa: Vậy: Ta gọi là dấu tích phân, a là cận dưới, b là cận trên. f(x)dx gọi là biểu thức dưới dấu tích phân . f(x) là hàm số dưới dấu tích phân. (công thức Newton – Laipnit) BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân S = F(b) – F(a) F(x) là một nguyên hàm của f(x) trên đ oạn [ a;b ] I. KHÁI NIỆM TÍCH PHÂN 2. Định nghĩa tích phân a) Định nghĩa: (công thức Newton – Laipnit) b) Chú ý: Nếu a = b thì Nếu a > b thì BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân I. KHÁI NIỆM TÍCH PHÂN 2. Định nghĩa tích phân c) Ví Dụ: 3. 4. 2. 1. a) Định nghĩa: b) Chú ý: BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân I. KHÁI NIỆM TÍCH PHÂN 2. Định nghĩa tích phân a) Định nghĩa: b) Chú ý: d) Nhận xét: Tích phân không phụ thuộc vào biến số Ý nghĩa hình học của tích phân: Cho hàm số y = f(x) liên tục và không âm trên đoạn [a;b]. Diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox, và hai đường thẳng x = a; x = b là: y = f(x) a b O y x . YN BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân Tính chất 1: a) Định nghĩa: b) Chú ý: II. TÍNH CHẤT CỦA TÍCH PHÂN II. TÍNH CHẤT CỦA TÍCH PHÂN 1. Các tích chất (k là h ằng số) Tính chất 2: Tính chất 3: BÀI 2 . TÍCH PHÂN (TIẾT 1) I. KHÁI NIỆM TÍCH PHÂN NỘI DUNG 1. Diện tích hình thang cong 2. Định nghĩa tích phân II. TÍNH CHẤT CỦA TÍCH PHÂN II. TÍNH CHẤT CỦA TÍCH PHÂN 2. Ví dụ: . . 1. Các tích chất . Tính các tích phân sau: H ƯỚNG DẪN: BẢNG NGUYÊN HÀM CỦNG CỐ: Phát biểu định nghĩa tích phân. - Ý nghĩa hình học của tích phân. - Các tính chất của tích phân. H ƯỚNG DẪN VỀ NHÀ: Đọc tr ước nội dung bài mới (p.III) - Xem và tự làm lại các ví dụ đã học. CHÂN THÀNH CẢM Ơ N QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH Phần mềm Graph 4.3
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_3_nguyen_ham_bai_2_tich_phan.ppt
bai_giang_dai_so_lop_12_chuong_3_nguyen_ham_bai_2_tich_phan.ppt

