Bài giảng Đại số Lớp 12 - Chương 3: Nguyên hàm - Bài 2: Tích phân - Đặng Thị Tố Uyên

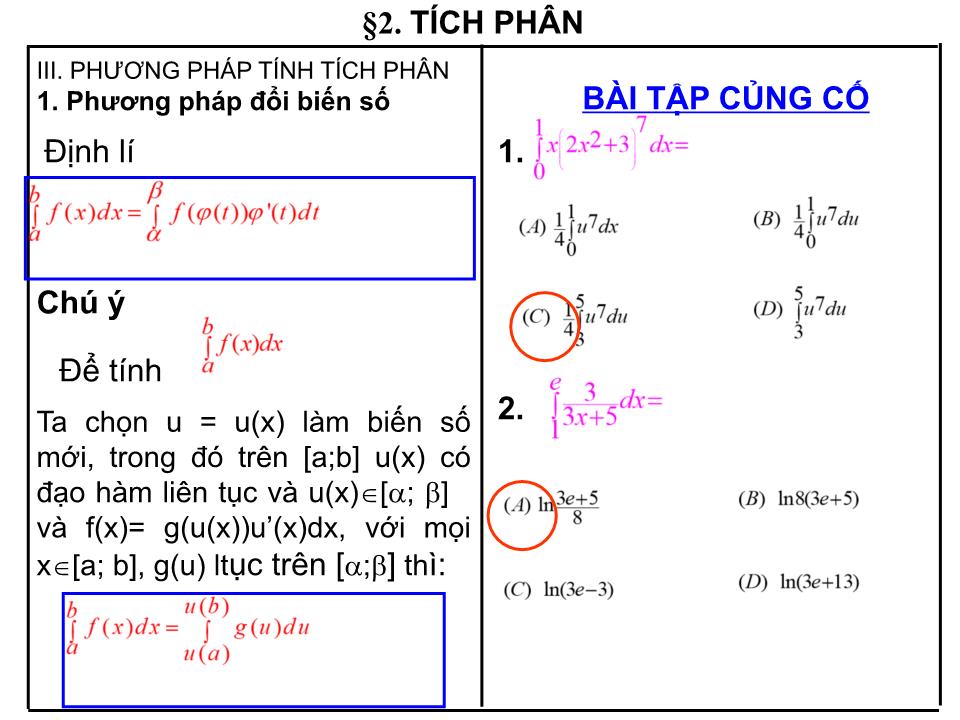
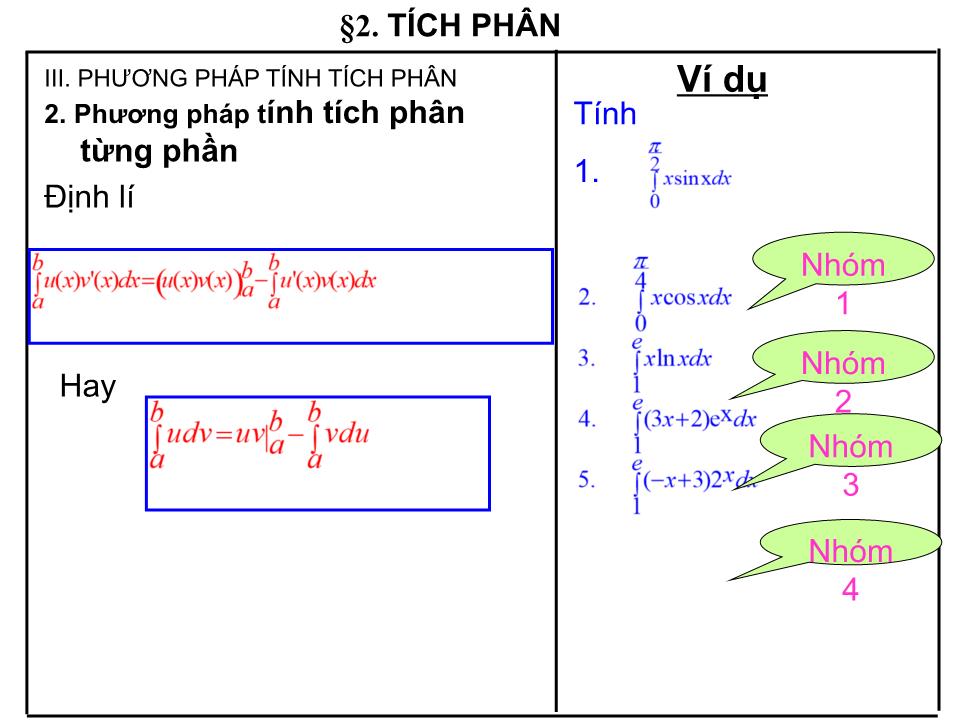
TRƯỜNG THPT ĐỊNH HOÁ 
TỔ TOÁN 
BÀI DẠY 
TÍCH PHÂN 
Người thực hiện: Đặng Thị Tố Uyên 
§2. TÍCH PHÂN 
Khái niệm tích phân 
 Tính chất của tích phân 
 Phương pháp tính tích phân 
a. Đặt u = 2x+1 . Biến đổi biểu thức (2x+1) 2 dx thành g(u)du . 
b. Tính và so sánh kết quả với I trong câu 2. 
KIỂM TRA BÀI CŨ 
Tính: 
a. 
Đặt u = 2x+1. Suy ra du = 2dx. 
Khi đó 
(2x+1)2dx = 
b. 
u(0) = 1, u(1) = 3 
Ta thấy 
 III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
 Phương pháp đổi biến số 
2. Phương pháp tính tích phân từng phần 
§2. TÍCH PHÂN 
 III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
1. Phương pháp đổi biến số 
§2. TÍCH PHÂN 
Định lí (SGK – 108) 
Cho hs f(x) liên tục trên đoạn [a; b]. Giả sử hs x = (t) có đạo hàm liên tục trên đoạn [ ; ] ( < ) sao cho a = ( ), b= () và a (t) b với mọi t [ ; ] . Khi đó: 
1. Tính 
§2. TÍCH PHÂN 
III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
1. Phương pháp đổi biến số 
Định lí. 
Ví dụ 
1. Tính 
Chú ý 
Để tính 
Ta chọn u = u(x) làm biến số mới, trong đó trên [a;b] u(x) có đạo hàm liên tục và u(x) [ ; ] và f(x)= g(u(x))u’(x)dx, với mọi x [a; b], g(u) lt ục trên [ ; ] th ì: 
2. Tính 
3. Tính 
4. Tính 
Nhóm 1 - 2 
Nhóm 3 - 4 
x = (t) a = ( ), b= () 
1. 
§2. TÍCH PHÂN 
III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
1. Phương pháp đổi biến số 
Định lí 
BÀI TẬP CỦNG CỐ 
Chú ý 
Để tính 
Ta chọn u = u(x) làm biến số mới, trong đó trên [a;b] u(x) có đạo hàm liên tục và u(x) [ ; ] và f(x)= g(u(x))u’(x)dx, với mọi x [a; b], g(u) lt ục trên [ ; ] th ì: 
2. 
HƯỚNG DẪN HỌC BÀI Ở NHÀ 
Định nghĩa và các tính chất của tích phân? 
 Phương pháp đổi biến số? 
 Làm bài tập : 3, 6.a) (SGK – 113) 
KIỂM TRA BÀI CŨ 
Tính: 
Đặt u= x 2 +2x-1, du =(2x+2)dx, x=1 thì u =-1, x=2 thì u=3 
Khi đó: 
2. Đặt 
Hãy tính 
= e 
Ta có pp tính tp từng phần 
§2. TÍCH PHÂN 
III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
2. Phương pháp t ính tích phân từng phần 
Định lí 
Ví dụ 
Tính 
1. 
Hay 
Nhóm 1 
Nhóm 2 
Nhóm 3 
Nhóm 4 
Nhóm 1 
Nhóm 2 
Nhóm 3 
Nhóm 4 
P(x)e x dx 
P(x)a x dx 
P(x)sinxdx 
P(x)cosxdx 
P(x)lnxdx 
u 
v’ 
§2. TÍCH PHÂN 
III. PHƯƠNG PHÁP TÍNH TÍCH PHÂN 
2. Phương pháp t ính tích phân từng phần 
Định lí 
Hay 
P(x) 
P(x) 
P(x) 
P(x) 
P(x) 
lnx 
cosx 
sinx 
a x 
e x 
Hãy chọn phương án em cho là đúng: 
Định lí 
(A) 3e 2 – 3 ; 
(D) Đáp án khác 
P(x)e x dx 
P(x)a x dx 
P(x)sinxdx 
P(x)cosxdx 
P(x)lnxdx 
u 
v’ 
P(x) 
P(x) 
P(x) 
P(x) 
P(x) 
lnx 
cosx 
sinx 
a x 
e x 
(B) 3e2 + 1 ; 
(C) 3e2 ; 
(D) Đáp án khác. 
Nếu em chọn đáp án (A) tức là: 
Thì em đã chọn sai đáp án. Có thể là do em bị sai lầm ở chỗ: 
Đặt u = e x , và v’ = 2x + 1 suy ra u’ =e x , v = x 2 + x 
Hãy xác định dạng tích phân để đặt u, v’ cho đúng và chọn phương án khác. 
Sai lầm 
Nếu em chọn đáp án (B) tức là: 
Thì em đã chọn sai đáp án. Có thể là do em bị sai lầm ở chỗ: 
Hãy xem lại công thức và chọn phương án khác. 
Nếu em chọn đáp án (C) tức là: 
Xin chúc mừng em đã chọn phương án đúng! 
Hãy trở lại bài toán khoanh vào phương án (C) và tiếp tục làm 2. 
(A) 3e 2 - 3;	(B) 3e 2 ;	(C) 3e 2 + 1 ; (D) Đáp án khác 
Nếu em chọn đáp án (D) tức là em có đáp án khác: 
Hãy trình bày phương án của em. 
Nếu em chọn đáp án (A) tức là: 
Thì em đã chọn sai đáp án. Có thể là do em bị sai lầm ở chỗ: 
Hãy tính lại và chọn phương án khác! 
Sai lầm 
Nếu em chọn đáp án (B) tức là: 
Xin chúc mừng em đã chọn phương án đúng! 
Hãy trở lại bài toán khoanh vào phương án (B) 
Nếu em chọn đáp án (C) tức là: 
Thì em đã chọn sai đáp án. Có thể là do em bị sai lầm ở chỗ: 
Hãy tính lại và chọn phương án khác! 
Sai lầm 
Sai lầm 
Nếu em chọn đáp án (D) tức là em có đáp án khác 
Hãy trình bày đáp án của em. 
Em đã làm sai! 
Trong các phương án trên chắc chắn có một phương án đúng. 
Hãy tính lại và chọn phương án khác. 
HƯỚNG DẪN HỌC BÀI Ở NHÀ 
Học lại các công thức tính nguyên hàm. 
 Các phương pháp tính nguyên hàm tích phân. 
 Làm các bài tập còn lại.