Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn
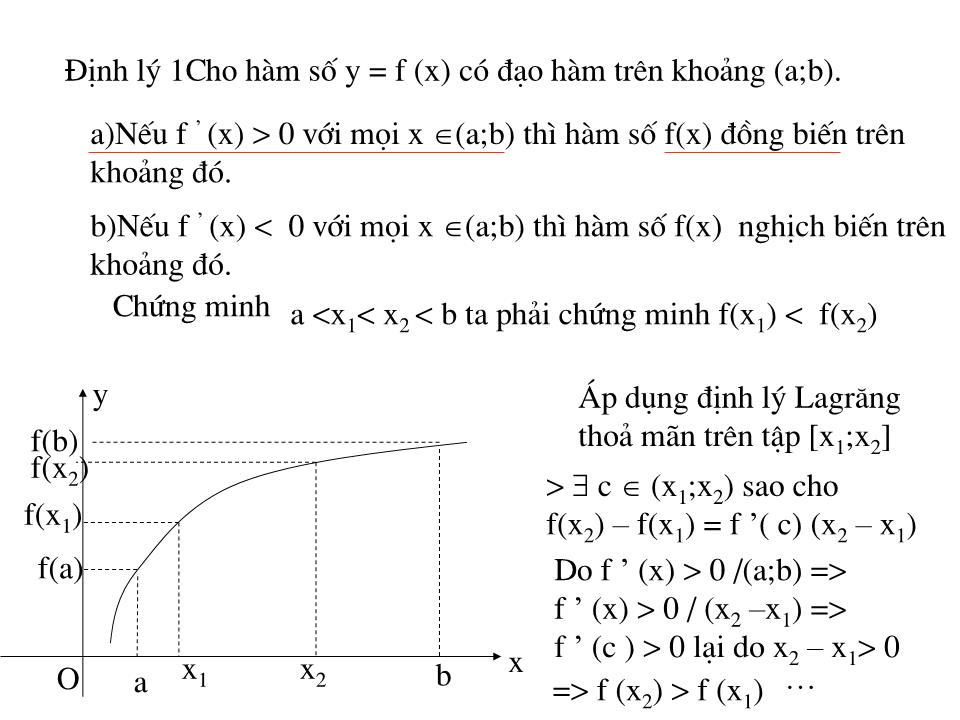
Định lý 1 Cho hàm số y = f (x) có đạo hàm trên khoảng (a;b).
a)Nếu f ’ (x) > 0 với mọi x ?(a;b) thì hàm số f(x) đồng biến trên
khoảng đó.
b)Nếu f ’ (x) < 0 với mọi x ?(a;b) thì hàm số f(x) nghịch biến trên
khoảng đó.
Định lý 2 Cho hàm số y = f (x) có đạo hàm trên khoảng (a;b).
a)Nếu f ’ (x) ? 0 với mọi x ?(a;b) thì hàm số f(x) đồng biến trên
khoảng đó.(Đẳng thức chỉ xảy ra tại hữu hạn điểm)
b)Nếu f ’ (x) ? 0 với mọi x ?(a;b) thì hàm số f(x) nghịch biến trên
khoảng đó.( Đẳng thức chỉ xảy ra tại hữu hạn điểm)

Trang 1

Trang 2
Trang 3

Trang 4
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn

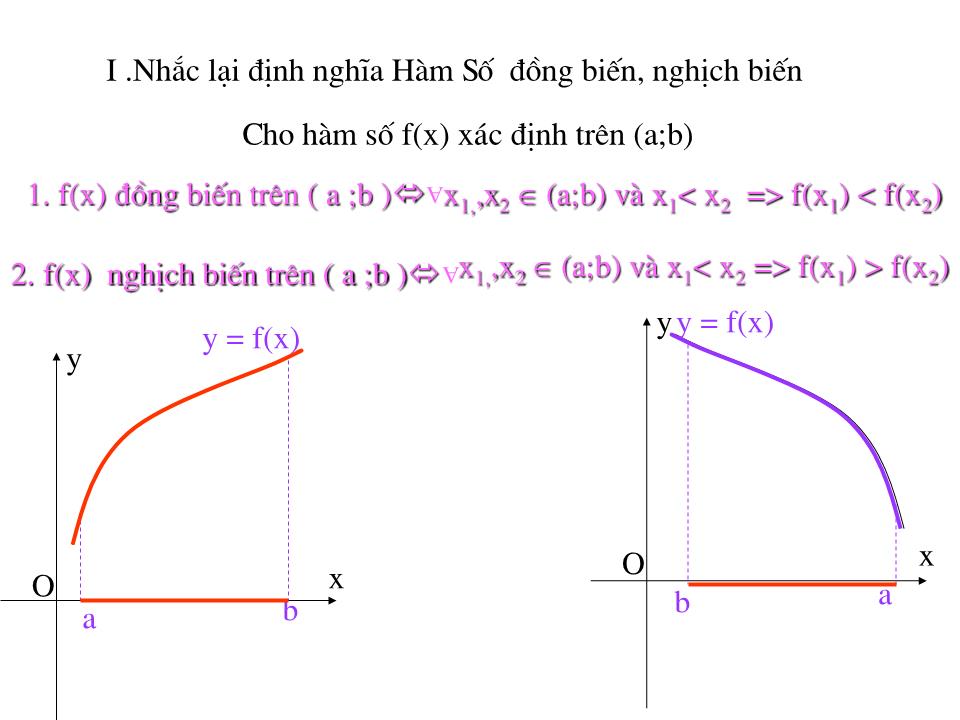
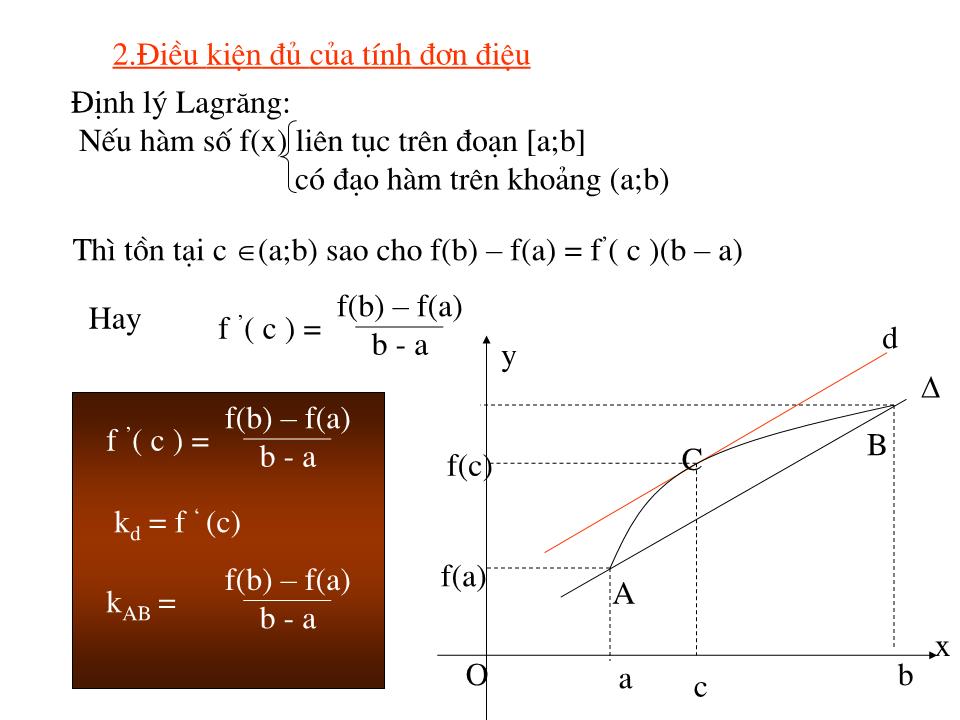
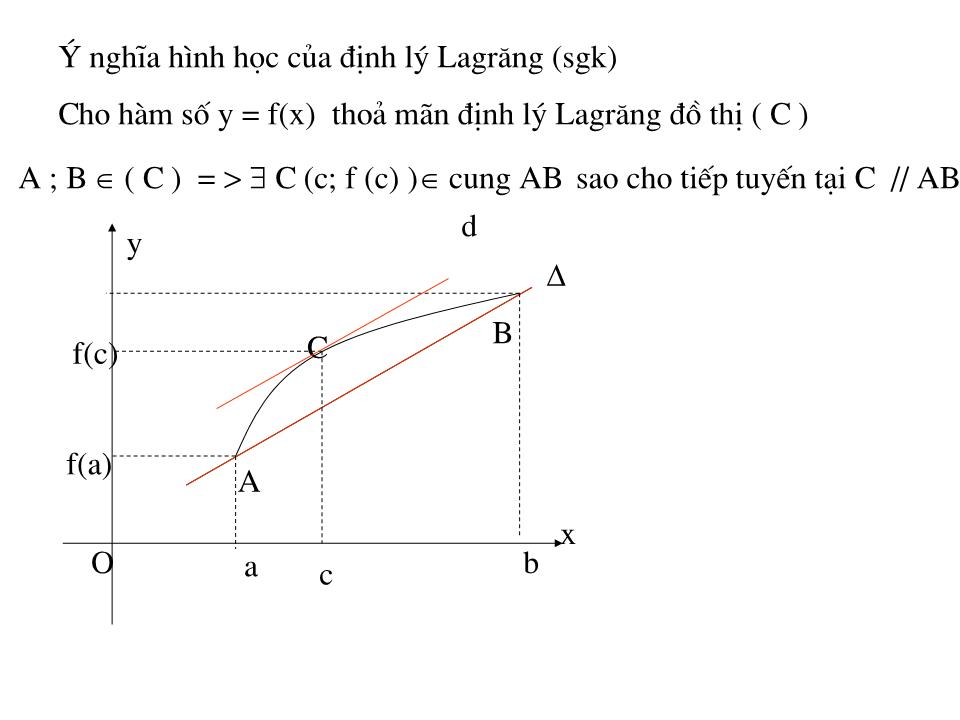
Bài tập trắc nghiệm Bài I;Khẳng đ ịnh : . Các hàm số sau đây luôn đ ồng biến trên từng khoảng xác đ ịnh của nó.Đúng hay sai ? 1) y = tgx 2) y = cotgx 3) y = 1 – 3x 4) y = lgx 5)y = lnx 7) y = e 3 ( ) x 6)y = 2 ( ) x 8) y = e x 9) y = log 0,5 (1- x) 10) y = 3 2 -5x Đ Đ Đ Đ Đ Đ S S S S Chương II: ứng dụng của đạo hàm Tiết 1: sự Đ ồng biến , nghịch biến của hàm số A 1. f(x ) đ ồng biến trên ( a ;b ) x 1, ,x 2 ( a;b ) và x 1 f(x 1 ) < f(x 2 ) I .Nhắc lại đ ịnh nghĩa Hàm Số đ ồng biến , nghịch biến A 2. f(x ) nghịch biến trên ( a ;b ) x 1, ,x 2 ( a;b ) và x 1 f(x 1 ) > f(x 2 ) Cho hàm số f(x ) xác đ ịnh trên ( a;b ) O x y O x y a b y = f(x ) b a y = f(x ) Nhận xét f(x ) đ ồng biến trên ( a;b ) => f ’ (x) = lim y x 0 0 trên ( a;b ) f(x ) ngh biến trên ( a;b ) => f ’ (x) = lim y x 0 0 trên ( a;b ) Chiều ngược lại có đ úng không ? Giới hạn này có là đ iều kiện đủ của tính đơn đ iệu ? 2.Điều kiện đủ của tính đơn đ iệu f(b ) – f(a ) b - a f ’ ( c ) = Đ ịnh lý Lagrăng : Nếu hàm số f(x ) liên tục trên đoạn [ a;b ] có đạo hàm trên khoảng ( a;b ) Th ì tồn tại c ( a;b ) sao cho f(b ) – f(a ) = f ’ ( c )(b – a) Hay A B y x O C a f(a ) b c f(c ) d k d = f ‘ (c) f(b ) – f(a ) b - a f ’ ( c ) = f(b ) – f(a ) b - a k AB = ý nghĩa hình học của đ ịnh lý Lagrăng ( sgk ) A B y x O C a f(a ) b c f(c ) d Cho hàm số y = f(x ) tho ả mãn đ ịnh lý Lagrăng đ ồ thị ( C ) A ; B ( C ) = > C (c; f (c) ) cung AB sao cho tiếp tuyến tại C // AB Đ ịnh lý 1 Cho hàm số y = f (x) có đạo hàm trên khoảng ( a;b ). a)Nếu f ’ (x) > 0 với mọi x ( a;b ) th ì hàm số f(x ) đ ồng biến trên khoảng đ ó . b)Nếu f ’ (x) < 0 với mọi x ( a;b ) th ì hàm số f(x ) nghịch biến trên khoảng đ ó . Chứng minh a <x 1 < x 2 < b ta phải chứng minh f(x 1 ) < f(x 2 ) á p dụng đ ịnh lý Lagrăng tho ả mãn trên tập [x 1 ;x 2 ] > c (x 1 ;x 2 ) sao cho f(x 2 ) – f(x 1 ) = f ’( c) (x 2 – x 1 ) Do f ’ (x) > 0 /( a;b ) => f ’ (x) > 0 / (x 2 –x 1 ) => f ’ (c ) > 0 lại do x 2 – x 1 > 0 x O f(b ) b f(a ) x 1 x 2 f(x 1 ) f(x 2 ) y a => f (x 2 ) > f (x 1 ) Đ ịnh lý 1 Cho hàm số y = f (x) có đạo hàm trên khoảng ( a;b ). a)Nếu f ’ (x) > 0 với mọi x ( a;b ) th ì hàm số f(x ) đ ồng biến trên khoảng đ ó . b)Nếu f ’ (x) < 0 với mọi x ( a;b ) th ì hàm số f(x ) nghịch biến trên khoảng đ ó . Mở rộng Đ ịnh lý 2 Cho hàm số y = f (x) có đạo hàm trên khoảng ( a;b ). a)Nếu f ’ (x) 0 với mọi x ( a;b ) th ì hàm số f(x ) đ ồng biến trên khoảng đó.(Đẳng thức chỉ xảy ra tại hữu hạn đ iểm ) b)Nếu f ’ (x) 0 với mọi x ( a;b ) th ì hàm số f(x ) nghịch biến trên khoảng đ ó .( Đẳng thức chỉ xảy ra tại hữu hạn đ iểm ) Đ ịnh lý 2 đ ịnh lý 1 n t n? Lợi ích của đ ịnh lý đ iều kiện đủ mở rộng ? Ví dụ 1: Tìm khoảng đ ồng biến hay nghịch biến của hàm số sau y = x 2 – 4x +6 Bài giải Tập xác đ ịnh : D = R Chiều biến thiên : y’ = 2x – 4 , Giải phương trình y’ = 0 2x – 4 = 0 x = 2 Dấu y’ X 2 y - 0 + Hàm số luôn luôn đ ồng biến trên khoảng ( 2 ;+ ) Và nghịch biến trên khoảng (- ; 2) Ví dụ 2: Tìm khoảng đ ồng biến hay nghịch biến của hàm số sau y = x 3 – 3x 2 +6 Bài giải Tập xác đ ịnh : D = R Chiều biến thiên : y’ = 3x 2 – 6x , Giải phương trình y’ = 0 3x 3 – 6x = 0 x = 0 v x = 2 Dấu y’ X 0 2 y + 0 - 0 + Hàm số luôn luôn đ ồng biến trên các khoảng ( - ; 0) ;(2;+ ) Và nghịch biến trên khoảng (0 ; 2) Ví dụ 3: Tìm khoảng đ ồng biến hay nghịch biến của hàm số sau y = - x 4 + 2x 2 +6 Bài giải Tập xác đ ịnh : D = R Chiều biến thiên : y’ = - 4x 3 +4x , Giải phương trình y’ = 0 -4x 3 + 4x = 0 x = 0 v x = 1 Dấu y’ Hàm số luôn luôn đ ồng biến trên các khoảng ( - ; 0) ;(2;+ ) Và nghịch biến trên khoảng (0 ; 2) X - -1 0 1 + y - 0 + 0 - 0 + Ví dụ 4: Xác đ ịnh chiều biến thiên của hàm số : Bài giải : * Tập xác đ ịnh : D = (- ;0)(0;+ ) * Đạo hàm y’ = y’ = 0 x = 1 X -1 0 1 y + 0 - || - 0 + Hàm số đ ồng biến trên các khoảng (- ;-1) ;(1;+ ) Hàm số nghịch biến trên các khoảng (-1;0) ;(0;1) Nêu Quy tắc xác đ ịnh chiều biến thiên của hàm số 3.Điểm tới hạn. Đ ịnh nghĩa : Cho hàm số y = f(x ) xác đ ịnh trên khoảng ( a;b ) và x 0 ( a;b).Điểm x 0 đư ợc gọi là một đ iểm tới hạn của hàm số f(x ) Nếu tại đ ó f ’(x) không xác đ ịnh hoặc x 0 là nghiệm của phương trình f ’(x) = 0. Qui tắc: Tìm tập xác đ ịnh của hàm số Tìm đ iểm tới hạn của hàm số xét dấu f ’(x) Kết luận về khoảng đ ồng biến , nghịch biến theo đ ịnh lý Bài tập về nh à. Từ bài 1 đ ến hết bài 4 sgk / Tr52 ,53
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_2_ung_dung_cua_dao_ham_bai_1.ppt
bai_giang_dai_so_lop_12_chuong_2_ung_dung_cua_dao_ham_bai_1.ppt

