Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn
Định nghĩa hàm số đồng biến, nghịch biến
Hàm số y = f(x) gọi là :
- Đồng biến trên (a; b) nếu:
- Nghịch biến trên (a; b) nếu:
* Hàm số y = f(x) gọi là đơn điệu trên (a; b) nếu nó đồng biến hoặc nghịch biến.
Để xét tính đơn điệu của hàm số y = f(x) ta đi xét dấu của f’(x)
Các bước xét tính đơn điệu:
Bước 1: Tìm TXĐ và tính y’
Bước 2: Xét dấu y’
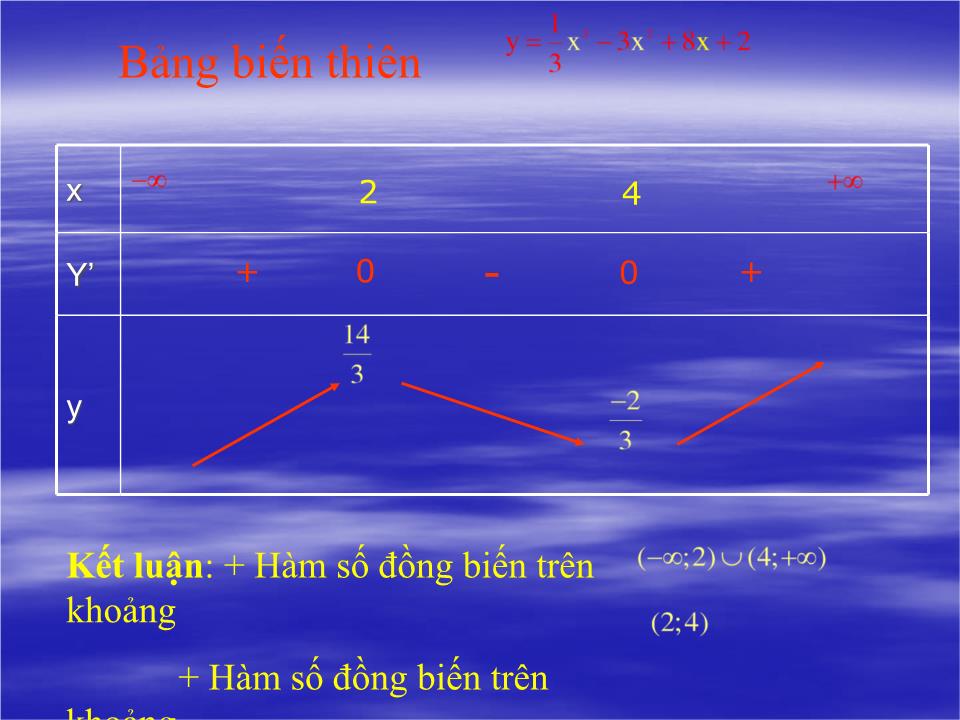
Bước 3: Lập bảng biến thiên và kết luận

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 2: Ứng dụng của đạo hàm - Bài 1: Sự đồng biến, nghịch biến của hàm số - Phạm Danh Hoàn

Chương II: ứng dụng của đạo hàm Bài 1: Sự đồng biến, nghịch biến của hàm số Phạm Danh Hoàn Thế nào là hàm số đồng biến, nghịch biến? Hàm số đ ơ n điệu? 1. Định nghĩa hàm số đồng biến, nghịch biến * Hàm số y = f(x) gọi là : - Đồng biến trên (a; b) nếu: - Nghịch biến trên (a; b) nếu: * Hàm số y = f(x) gọi là đ ơ n điệu trên (a; b) nếu nó đồng biến hoặc nghịch biến. Cách khác để xét tính đ ơ n điệu của hàm số? 2. Điều kiện đủ của tính đ ơ n điệu Định lý1: (Lagrange) Nếu hàm số f(x) liên tục trên [a; b] và có đạo hàm trên (a;b) thì tồn tại c (a;b) sao cho: ý nghĩa của định lý lagrange XÉT CUNG AB CỦA ĐỒ THỊ HÀM SỐ Y = F(X) VỚI A(A; F(A)), B(B;F(B)) f(c) C c Hệ số góc của cát tuyến AB Hệ số góc của tiếp tuyến của cung AB tại điểm C(c; f(c)) bằng hệ số góc của cát tuyến AB. A B a f(a) f(b) b x y O * Dấu hiệu (điều kiện đủ) của tính đ ơ n điệu Định lý 2 : Cho hàm số y = f(x) có đạo hàm trên (a; b). a) Nếu f’(x) < 0 x (a; b) thì f(x) nghịch biến trên (a; b) b) Nếu f’(x) > 0 x (a; b) thì f(x) đồng biến trên (a; b) Để xét tính đ ơ n điệu của hàm số ta đi xét dấu của f’(x) Ví dụ 1: Xét tính đồng biến, nghịch biến (đ ơ n điệu) của hàm số sau TXĐ: D = R x Y’ y 2 4 0 0 + - + Bảng biến thiên Kết luận : + Hàm số đồng biến trên khoảng + Hàm số đồng biến trên khoảng Ví dụ 2: Xét tính đồng biến, nghịch biến (đ ơ n điệu) của hàm số sau x Y’ y 1 + + Bảng biến thiên Kết luận : + Hàm số đồng biến trên khoảng Để xét tính đ ơ n điệu của hàm số y = f(x) ta đi xét dấu của f’(x) Các b ư ớc xét tính đ ơ n điệu: B ư ớc 1 : Tìm TXĐ và tính y’ B ư ớc 2 : Xét dấu y’ B ư ớc 3 : Lập bảng biến thiên và kết luận XIN CHÂN THÀNH CẢM ƠN HẾT
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_2_ung_dung_cua_dao_ham_bai_1.ppt
bai_giang_dai_so_lop_12_chuong_2_ung_dung_cua_dao_ham_bai_1.ppt

