Bài giảng Đại số Lớp 12 - Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số logarit - Bài 6: Bất phương trinh mũ và logarit
Bất phương trình lôgarit cơ bản:
Bất phương trình lôgarit cơ bản có dạng loga x > b
( hoặc logax ≥ b, loga x ≥ b, logax < b, logax ≤ b), với a > 0, a≠ 1.
Xét bất phương trình: loga x > b
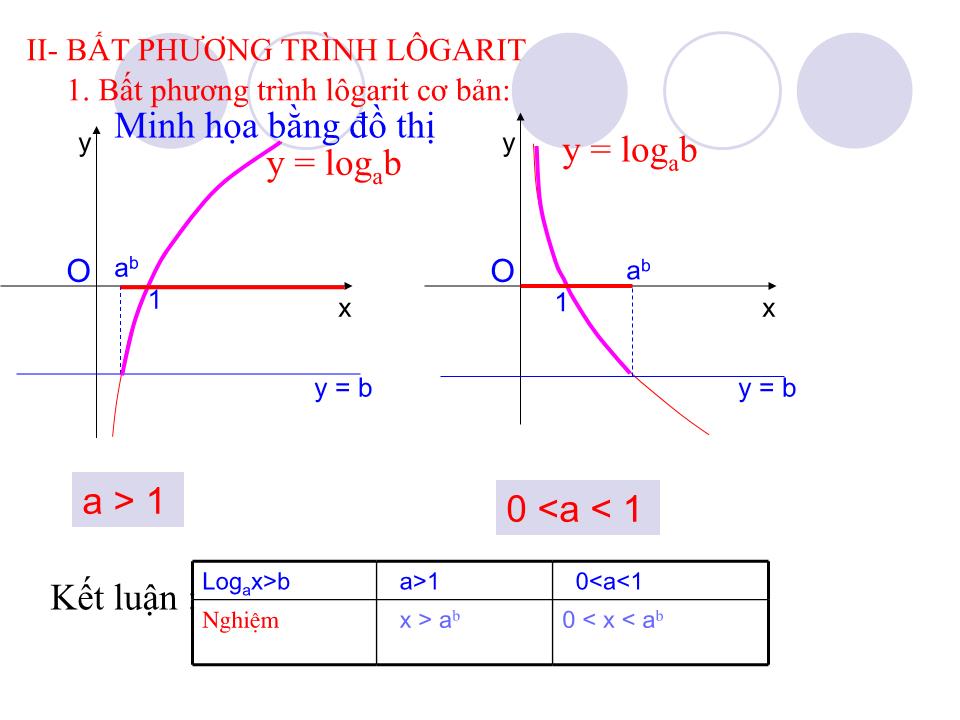
Trường hợp a > 1, ta có
loga x > b x > ab
Trường hợp 0 < a < 1, ta có
loga x > b 0 < x < ab.
Bất phương trình logarit đơn giản
Ta xét 1 số bất PT logarit đơn giản, để giải nó: ta có thể biến đổi để đưa về bất PT logarit cơ bản hoặc bất PT đại số

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Bạn đang xem tài liệu "Bài giảng Đại số Lớp 12 - Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số logarit - Bài 6: Bất phương trinh mũ và logarit", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số logarit - Bài 6: Bất phương trinh mũ và logarit

§6: BẤT PH ƯƠ NG TRINH MŨ VÀ LOGARIT GV: VŨ THỊ BÍCH THU Tổ: Toán- Tin §6. BẤT PH ƯƠ NG TRÌNH MŨ VÀ BẤT PH ƯƠ NG TRÌNH LÔGARIT II- bất ph ươ ng trình lôgarit 1. Bất ph ươ ng trình lôgarit c ơ bản: Bất ph ươ ng trình lôgarit c ơ bản có dạng log a x > b ( hoặc log a x ≥ b, log a x ≥ b, log a x 0, a ≠ 1. Xét bất ph ươ ng trình: log a x > b Tr ư ờng hợp a > 1, ta có log a x > b x > a b Tr ư ờng hợp 0 < a < 1, ta có log a x > b 0 < x < a b . II- BẤT PH ƯƠ NG TRÌNH LÔGARIT 1. Bất ph ươ ng trình lôgarit c ơ bản: Minh họa bằng đồ thị O x y 1 a b y = b y = log a b a > 1 O x y 1 a b y = b y = log a b 0 <a < 1 Kết luận : Log a x>b a>1 0<a<1 NghiÖm x > a b 0 < x < a b II- BẤT PH ƯƠ NG TRÌNH LÔGARIT 1. Bất ph ươ ng trình lôgarit c ơ bản Ví dụ: a) log 2 x > 7 x > 2 7 x > 128 Hãy lập bảng t ươ ng tự cho các bất PT: log a x ≥ b, log a x < b, log a x ≤ b Log a x ≥ b a>1 0 <a <1 Nghiệm x ≥ a b 0 < x ≤ a b II- BẤT PH ƯƠ NG TRÌNH LÔGARIT 1. Bất ph ươ ng trình lôgarit c ơ bản Log a x < b a > 1 0 < a <1 Nghiệm 0 < x< a b x > a b Log a x ≤ b a> 1 0 < a < 1 Nghiệm 0 <x ≤ a b x ≥ a b 2. Bất ph ươ ng trình logarit đ ơ n giản *) Ta xét 1 số bất PT logarit đ ơ n giản, để giải nó: ta có thể biến đổi để đ ư a về bất PT logarit c ơ bản hoặc bất PT đại số II- BẤT PH ƯƠ NG TRÌNH LÔGARIT 2. Bất ph ươ ng trình lôgarit ®¬n gi¶n *) Ví dụ: Ví dụ 1: Giải bất PT log 0,5 (5x + 10) < log 0,5 (x 2 + 6x + 8).(1) Giải Điều kiện của BPT đã cho là: x > -2 Vì c ơ số 0,5 < 1 nên ta có BPT t ươ ng đ ươ ng với BPT nào (1) 5x+10 > x 2 + 6x + 8 x 2 + x – 2 < 0 -2 < x < 1 Kết hợp với điều kiện, ta đ ư ợc tập nghiệm của BPT ? Kết hợp đk, Tập nghiệm của BPT là: (-2 ; 1) II- BẤT PH ƯƠ NG TRÌNH LÔGARIT 2. Bất ph ươ ng trình lôgarit Ví dụ 2 : Giải bất ph ươ ng trình log 2 ( x - 3) + log 2 (x - 2) ≤ 1 (2) Giải Điều kiện xác định của BPT là: x > 3 (2) log 2 [(x-3)(x-2)] ≤ 1 (2) (x-3)(x-2) ≤ 2 x 2 – 5x +4 ≤ 0 1 ≤ x ≤ 4 Kết hợp với Đk ta có điều gì? Kết hợp với đk ta có 3 < x ≤ 4 Kết luận : Tập nghiệm của BPT là (3; 4] CỦNG CỐ Bài 1: Tập nghiệm của BPT log (x - 1) ≥ -2 là Bài 2: Tập nghiệm của BPT (x – 5)(log x + 1) = 1 là Bài 3: Tập nghiệm của BPT log 2 (3 x – 2) < 0 là a) x ≤ 10 b) 1 < x < 10 c) 1 < x ≤ 10 d) 1 ≤ x ≤ 10 a) (1/10;5] d) (1/10;5) c) [1/10;5] b) [1/10;5) a) x > 1 b) x < 1 c) 0 < x < 1 d) log 3 2 < x < 1 Bài tập về nhà Bài 2: Trang 90( SGK) Chào tạm biệt và hẹn gặp lại
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_2_ham_so_luy_thua_ham_so_mu_v.ppt
bai_giang_dai_so_lop_12_chuong_2_ham_so_luy_thua_ham_so_mu_v.ppt

