Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Nguyễn Thị Yến
Ví dụ1: Khảo sát hàm số: y= x3-2x2+x+4
1) Tập xác định: D=R
2) Sự biến thiên:
a) Chiều biến thiên:
y’=3x2-4x+1
y’ = 0 x= 1, x=1/3
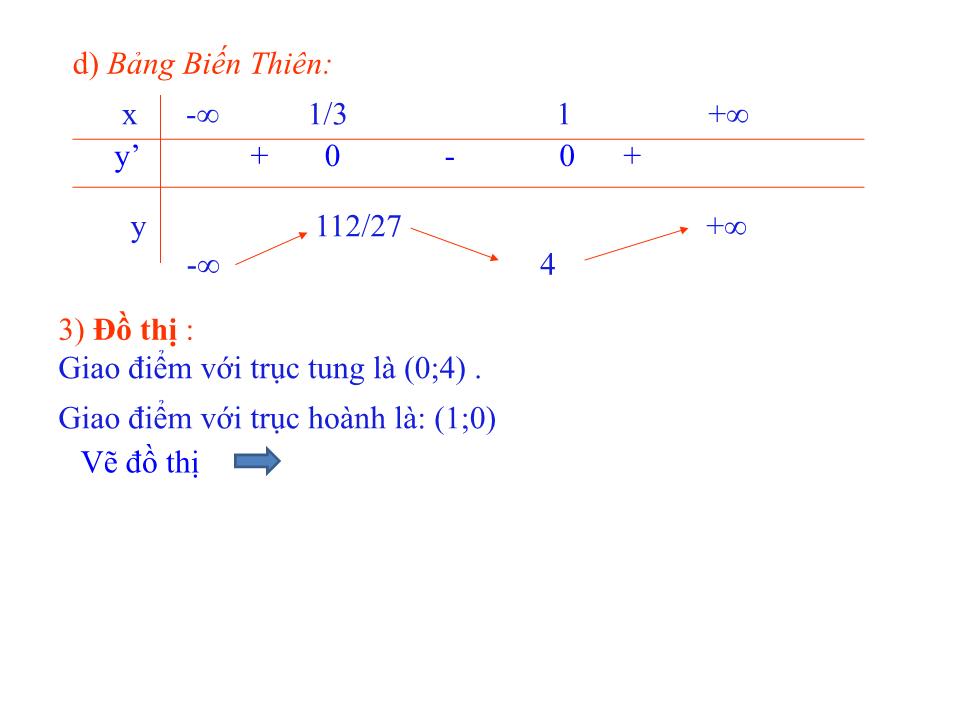
Hàm số đồng trên (-∞;1/3) và (1;+) ,
Hàm số nghịch biến trên (1/3;1)
b) Cực trị:
Hàm số đạt cực tiểu tại x= 1,yCT = 4
Hàm số đạt cực đại tại x = 1/3 ,yCĐ = 112/27.
c) Tâm đối xứng của đồ thị
y’’=6x-4
y’’ = 0 x=2/3
Hàm số có tâm đối xứng là I(2/3 ;110/27);

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
Trang 6

Trang 7
Trang 8

Trang 9

Trang 10
Bạn đang xem tài liệu "Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Nguyễn Thị Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Nguyễn Thị Yến

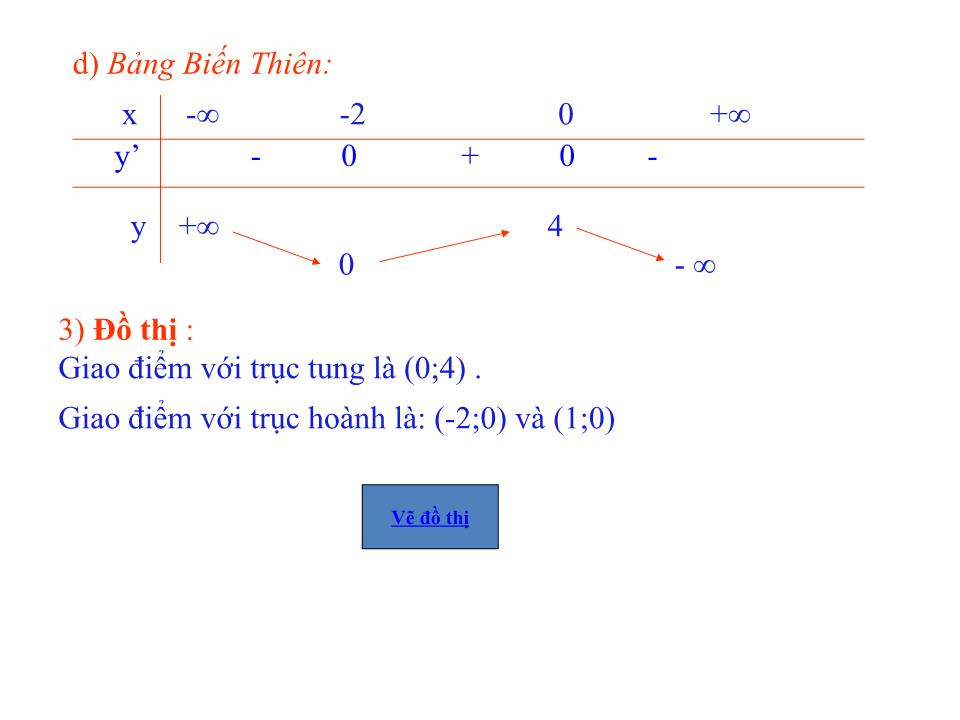
SV: Nguyễn Thị Yến 20/04/1991 Lớp: Toán K44D Trường Đại học sư phạm Thái Nguyên Hãy nêu sơ đồ khảo sát hàm số? I.S ơ đồ khảo sát hàm số 1, Tìm TXĐ của hàm số 2, Khảo sát sự biến thiên của hàm số a, Xét chiều biến thiên của hàm số * Tính đạo hàm * Tìm các điểm tại đú đạo hàm y’ bằng 0 hoặc khụng xỏc định. * Xét dấu của đạo hàm y’ và suy ra chiều biến thiên của hàm số. b, Tính các cực trị c, Tìm các giới hạn của hàm số tại vụ cực, cỏc giới hạn vụ cực và tỡm tiệm cận (nếu cú) d, Lập bảng biến thiên (ghi cỏc kết quả tỡm được vào bảng biến thiờn) 3 ) Vẽ đồ thị * Giao với các trục toạ độ * Các điểm đặc biệt (điểm cực trị , ...) * Vẽ đồ thị Khảo sát và vẽ đồ thị của hàm số bậc ba y = ax 3 + bx 2 + cx + d (a 0) Ví dụ1 : Khảo sát hàm số: y= x 3 -2x 2 +x+4 1) Tập xác định : D= R 2) Sự biến thiên: a) Chiều biến thiên : y’=3x 2 -4x+1 y’ = 0 x= 1, x=1/3 Hàm số đồng trên (-∞;1/3) và (1;+ ) , Hàm số nghịch biến trên (1/3;1) b) Cực trị: Hàm số đạt cực tiểu tại x= 1,y CT = 4 Hàm số đạt cực đại tại x = 1/3 ,y CĐ = 112/27. c) Tâm đối xứng của đồ thị y’’=6x-4 y’’ = 0 x=2/3 Hàm số có tâm đối xứng là I(2/3 ;110/27); x - 1/3 1 + y’ + 0 - 0 + y 112/27 + -∞ 4 Vẽ đồ thị d) Bảng Biến Thiên: 3) Đồ thị : Giao điểm với trục tung là (0;4) . Giao điểm với trục hoành là: (1;0) Ví dụ2 : Khảo sát hàm số: y= -x 3 -3x 2 +4 1) Tập xác định : D= R 2) Sự biến thiên: a) Chiều biến thiên : y’=-3x 2 -6x y’ = 0 x= 0, x=-2 Hàm số đồng trên (-2;0), Hàm số nghịch biến trên ( -∞;-2 ) và (0; +∞) b) Cực trị: Hàm số đạt cực tiểu tại x= -2,y CT = 0 Hàm số đạt cực đại tại x = 0 ,y CĐ = 4. c) Tâm đối xứng của đồ thị y’’=-6x-6 y’’ = 0 x=-1 Hàm số có tâm đối xứng là I(-1 ;2); x - -2 0 + y’ - 0 + 0 - y +∞ 4 0 - ∞ d) Bảng Biến Thiên: 3) Đồ thị : Giao điểm với trục tung là (0;4) . Giao điểm với trục hoành là: (-2;0) và (1;0) Vẽ đồ thị Bài tập về nhà Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: 1. y = 4x 3 – 2x 2 +-5x +3 2. y = x 3 – x 2 + 3x - 1 Em xin chân thành cảm ơn Chúc thầy mạnh khỏe công tác tốt Chúc các bạn đạt kết quả cao trong kỳ thi tới Th ái Nguyên, ngày 21/04/2012
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_1_cuc_tri_cua_ham_so_bai_5_kh.ppt
bai_giang_dai_so_lop_12_chuong_1_cuc_tri_cua_ham_so_bai_5_kh.ppt

