Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

VẼ ĐỒ THỊ CỦA HÀM SỐ 
KHẢO SÁT SỰ BIẾN THIÊN VÀ 
VẼ ĐỒØ THỊ CỦA MỘT SỐ HÀM ĐA THỨC 
I. KHẢO SÁT SỰ BIẾN THIÊN VÀ 
1. Các bứ ơ c khảo sát hàm số y=f(x ) 
Tập xác định: ( nhận định thêm về hàm số chẳn, hàm số lẻ,hàm số tuần hoàn) 
ii) Sự biến thiên: 
1) Tìm giới hạn ,tiệm cận ( nếu có ) 
3) Lập BBT xác định các khoảng đồng biến, nghịch biến 
iii) Đồ thị: 
 Tìm giao điểm (nếu có) của đồ thị với trục tung và trục hoành các điểm phụ và vẽ đồ thị đi qua các điểm đã tìm. 
2) Chiều biến thiên : ( Tính y’, kháo sát dấu y’ ) 
4) Cực trị ( nếu có ) 
5)Điểm uốn có hoành độ là nghiệm của đạo hàm cấp 2 
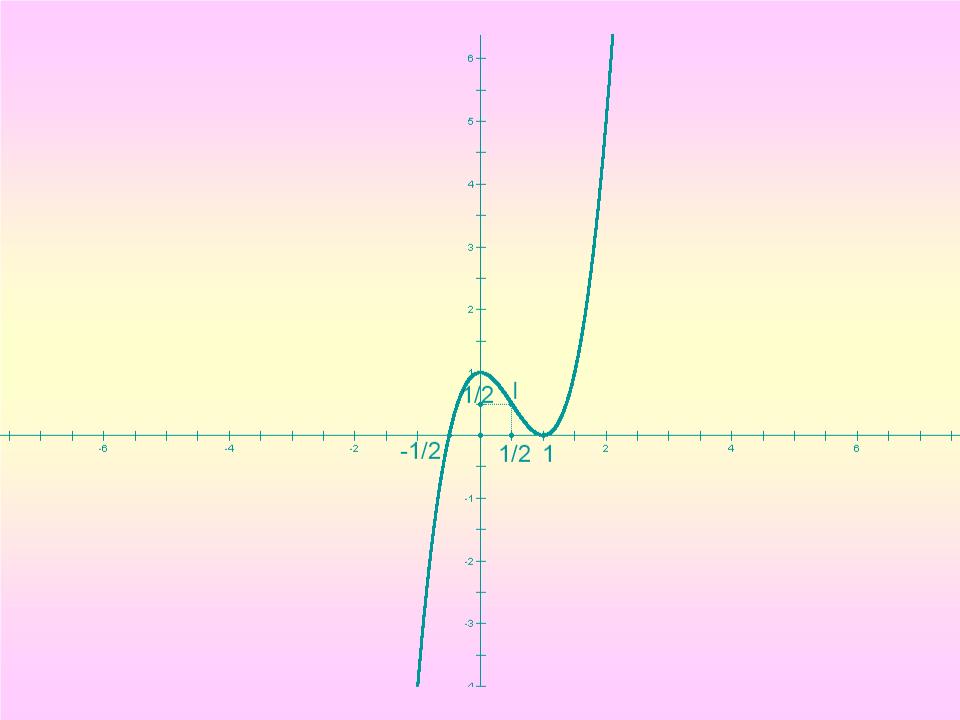
Ví dụ 1: Khảo sát hàm số: y= 2x 3 -3x 2 +1 
Giải: 
TXĐ: D=R 
c) Cực trị: 
Hàm số đạt cực đại tại x=0; y CĐ =1, cực tiểu tại x=1;y CT =0. 
Đồ thị không có tiệm cận 
2. Hàm số bậc 3: y=ax 3 +bx 2 +cx+d (a 0) 
a) Giới hạn: 
b) Chiều biến thiên 
2) Sự biến thiên: 
y’ = 6x 2 -6x, y’=0 x=0 hoặc x=1. 
y’ >0 trên (- ;0) và (1; + ), y’ <0 trên (0;1) 
Ví dụ 2: Khảo sát hàm số y = -x 3 +3x 2 -3x+2 
x - 0 1 + 
y’ + 0 - 0 + 
y - 1 0 + 
d)Bảng biến thiên 
 y’’=12x-6 ,y’’=0 x= 1/2 
e ) điểm uốn 
I(1/2;1/2) 
3) Đồ thị: y=0 (x-1) 2 (2x+1)=0 x=1 , x=-1/2. 
x=0 ,y = 1. (1;0) và(-1/2;0) là giao điểm của đồ thị với 
trục hoành và . (0;1) giao điểm của đồ thị với trục tung . 
Điểm uốn 
Chú ý 1: Đồ thị hàm số nhận điểm uốn làm tâm 
đối xứng. Thật vậy: 
y =2x 3 -3x 2 +1 
Chú ý 2: Tiếp tuyến tại điểm uốn có phương trình: 
Tịnh tiến hệ trục toa độ theo véctơ: , với 
 là hàm số lẻ trên R nên đò thị hàm số này nhận điểm I làm tâm đối xứng. 
Ví dụ2: Khảo sát hàm số y = -x 3 +3x 2 -3x+2 
Giải: 
 2)Sự biến thiên: 
x - 1 + 
y’ - 0 - 
y 
+ 
- 
d)Bảng biến thiên 
c) Giới hạn: 
Đồ thị hàm số không có tiệm cận 
a) Chiều biến thiên: y ’ = -3(x 2 -2x+1) = -3(x-1) 2 y’ ≤ 0 
b) Cực trị: Hàm số không có cực trị 
 dấu ‘= ‘ xảy ra khi x=1 hàm số nghịch biến trên R. 
1) TXĐ : R 
y’’=-6(x-1) ,y’’=0 x=1 
 Đ.uốn 
I(1;1) 
e) điểm uốn 
3)Đồ thị: Giao điểm với trục Ox: (2;0) 
 Giao điểm với trục Oy: (0;2) 
Tiềp tuyến tại điểm uốn(1;1) là : y=1 
Chú ý: 
y 
x 
Tóm tắt: y =ax 3 +bx 2 +cx+d (a 0) 
Tập xác định R . 
Đồ thị luôn có 1 điểm uốn và nhận điểm uốn làm tâm đối xứng. ( Chứng minh xem như bài tập) 
y’= 3ax 2 +2bx+c . 
Nếu y’=0 có hai nghiệm phân biệt thì hàm số có cực đại 
và cực tiểu và đồ thị có hai dạng sau: 
a>0 
a<0 
Nếu y’ =0 có nghiệm kép , hàm số đơn điệu , tiếp tuyến tại điểm uốn cùng phương với trục hoành. Đồ thị có dạng 
sau: 
Nếu y’ =0 vô nghiệm , hàm số đơn điệu . Đồ thị có dạng sau: 
8 
6 
4 
2 
-2 
-4 
-6 
-8 
-10 
-5 
5 
10 
8 
6 
4 
2 
-2 
-4 
-6 
-8 
-10 
-5 
5 
10 
8 
6 
4 
2 
-2 
-4 
-6 
-8 
-10 
-5 
5 
10 
8 
6 
4 
2 
-2 
-4 
-6 
-8 
-10 
-5 
5 
10 
Đơn điệu 
y CĐ .y CT > 0 
Nhận Xét: y=ax 3 +bx 2 +cx+d (a 0) 
Nếu hàm số có cực đại và cực tiểu: A(x CT ,y CT ), B(x CĐ ,y CĐ ) thì chia y cho y’ ta có : 
2) Số giao điểm của đồ thị và trục hoành: (bằng số nghiệm của phương trình hoành độ giao điểm y =0). 
Số nghiệm 
Hàm số 
1 
2 
y CĐ .y CT =0 
3 
 y CĐ .y CT < 0 
 Do đó , y = α x+ β l à đường th ẳng đi qua hai đ i ểm c ực đại v à c ực ti ểu c ủa đồ th ị . 
y = y’(ux+v) + α x+ β y CT = α x CT + β v à y CĐ = α x CĐ + β . 
2) Hàm số y =ax 4 +bx 2 +c (a 0) 
Ví dụ1 : Khảo sát hàm số: y= x 4 -2x 2 -3 
1) Tập xác định : D= R , hàm số chẳn 
2) Sự biến thiên: 
a) Chiều biến thiên : y’=4x 3 -4x , y’ = 0 x=-1,x=0,x=1 
y’ > 0 trên (-1;0)và (1;+ ) , y’ < 0 trên (0;1) và (- ;-1) 
b) Cực trị: Hàm số đạt cực tiểu tại x= 1,y CT = -4 và 
đạt cực đai tại x = 0 ,y CĐ = -3. 
c) Giới hạn : 
Đồ thị không có tiệm cận: 
hambac4.gsp 
x - -1 0 1 + 
y’ - 0 + 0 - 0 + 
y + -3 + 
 -4 -4 
e) Tính lồi lõm , điểm uốn: 
y’’=12x 2 -4 , y’’ = 0 
x - + 
y’’ + 0 - 0 + 
ĐT lõm Đ.uốn lồi Đ.uốn lõm 
( ;-32/9) 
( ;-32/9) 
d) Bảng Biến Thiên: 
3) Đồ thị : Đồ thị nhận Oy là trục đối xứng và cắt oy tại 
(0;-3) . ĐT cắt Ox tai hai điểm 
8 
6 
4 
2 
-2 
-4 
-6 
-8 
-10 
-5 
5 
10 
y=a 
x 
4 
+b 
x 
2 
+c 
Ví dụ 2: Khảo sát hàm số: 
Giải: 
TXĐ : D=R , hàm số chẳn. 
Sự biến thiên: 
a)Chiều biến thiên: y’=-2x 3 -2x=-2x(x 2 +1)=0 x=0. 
Y’ > 0 trên (- ;0) , y’ < 0 trên (0;+ ) 
b) Cực trị: Điểm cực đại x = 0; y CĐ =3/2. 
c) Giới hạn : 
 Đồ thị không có tiệm cận 
BBT 
x - 0 + 
y’ + 0 - 
y 
3/2 
- 
- 
e) Tính lồi lõm, điểm uốn: 
Y’’=-2(3x 2 +1) < 0 x R 
x - + 
y’’ - 
ĐồThị 
lồi 
3)Đồ thị 
Đồ thị nhận Oy làm trục đố xứng ; y = 0 x= 1 
ĐT cắt Ox tại (-1; 0) và (1;0) 
5 
4 
3 
2 
1 
-1 
-2 
-3 
-4 
-5 
-8 
-6 
-4 
-2 
2 
4 
6 
8 
y=a 
x 
4 
+b 
x 
2 
+c 
Tóm tắt: y =ax 4 +bx 2 +c (a 0) 
y’=0 có 
3 nghiệm 
Phân biệt 
y’=0 có 
1 nghiệm 
a>0 
a<0 
Bài tập: 
1) Bài tập SGK 
2)Chứng minh đồ thị hàm số bậc 3 nhận điểm uốn làm tâm đối xứng. 
3) Cho hàm số y = 4x 3 -ax. Tìm a sao cho ‌ y ‌ ≤1 v ới mọi x [-1;1]. Khảo sát hàm số tìm được. 
4) Tìm hàm số y = 4x 3 +ax 2 +bx+c sao cho: cho ‌ y ‌ ≤1 với mọi x [-1;1]. 
5) Cho hàm số y = x 4 +4x 3 +4x 2 + m. 
 i) m=0 khảo sát hàm số. Chứng minh rằng đồ thị có trục đố xứng. 
ii) Giải biện luận phương trình y =0. 
iii) Tìm m để đồ thị cắt trục hoành 4 điểm phân biệt có hoành độ lập thành cấp số cộng 
Hàm số 
Ví dụ 1 : Khảo sát hàm số: 
Giải:i) Tập xác định : 
2) sự biến thiên: 
a) Chiều biến thiên: 
Y’ không xác định tại x=-1/2 
Y’<0 , x -1/2 .Vậy hàm số nghịch biến trên các 
Khoảng (- ;-1/2) và (-1/2;+ ). 
b) Cực trị : hàm số không có cực trị. 
c) Giới hạn: 
Vậy :đường thẳng :x=-1/2 là tiệm cận đứng 
Vậy :đường thẳng :y=-1/2 là tiệm cận ngang 
d) Bảng biến thiên 
X - -1/2 + 
Y’ - - 
y 
-1/2 
- 
+ 
-1/2 
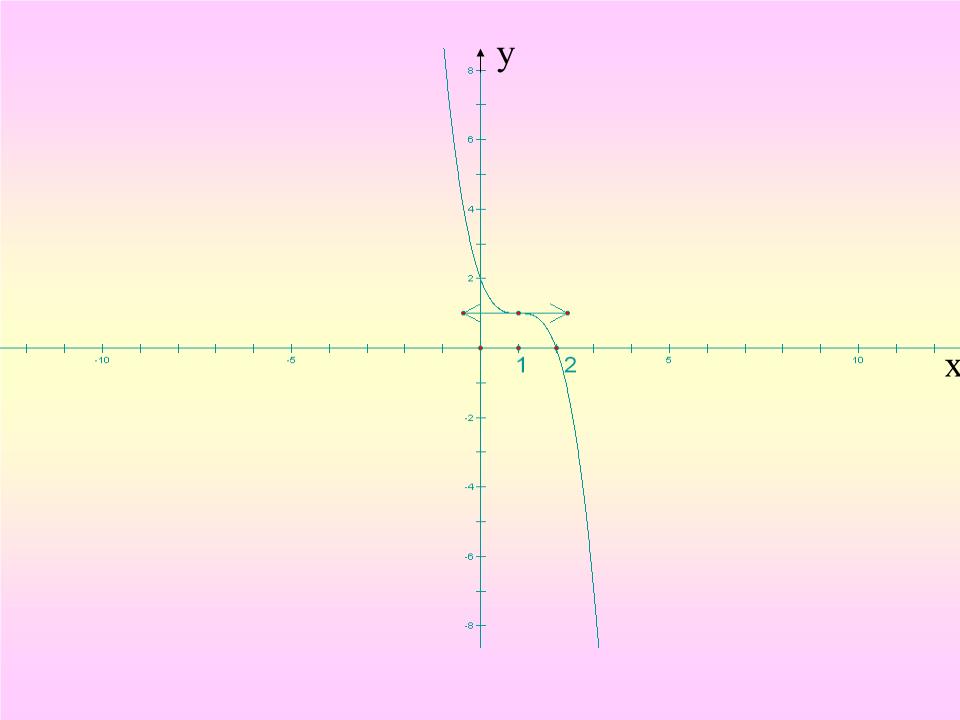
3) Đồ thị: Đồ thị cắt trục tung tại A(0;2), cắt trục hoành 
Tại B(2;0). 
Chú ý: Đồ thị nhận giao điểm hai tiệm cận I (-1/2;-1/2) 
 làm tâm đối xứng.Tịnh tiến hệ trục toạ độ theo véctơ 
OI thì ta có phương trình: 
Ví dụ 2) Khảo sát hàm số: 
Giải: 
1) Tập xác định: R\{-1} 
2) Sự biến thiên: 
a) Chiều biến thiên: 
y’>0 trên (- ;-1) và (-1; + ) 
b) Cực trị: hàm số không có cực trị. 
c) Giới hạn: 
Đồ thị có tiệm cận đứng : x = -1 
Đồ thị có tiệm cận ngang: y = 2 
d) Bảng biến thiên: 
x - -1 + 
y’ + + 
y 
2 
+ 
- 
2 
3) Đồ thị: giao điểm của đồ thị với trục tung: (0;-1). 
 Giao điểm của đồ thị với trục hoành: (1/2;0). 
Tóm tắt: 
c 0 
Nếu ad –bc= 0 thì y = a /c 
Nếu ad-bc 0 thì đồ thị có tiệm cận đứng: x = -d/c. 
 Tiệm cận ngang: y = a/c 
Giao điểm của hai tiệm cận ( -d/c;a/c) là tâm đối xứng 
TXĐ: 
Đồ thị có hai dạng sau: 
ad-bc>0 
ad-bc<0 
Ta có: 
Tịnh tiến hệ trục toạ độ theo OI=(-d/c;a/c) 
.Ta có hàm số 
Là hàm số lẻ , đồ thị 
Có tâm đối xứng là I(-d/c;a/c) 
Hàm số: 
aa’ 0 
Ví dụ1 : Khảo sát hàm số: 
1) Tập xác định: R \{1}. 
2) Sự biến thiên 
Chiều biến thiên: 
y’ =0 x = -1, x = 3.Dấu y’ là dấu của x 2 -2x-3. 
Y’> 0 nếu x 3 và y’<0 nếu -1< x < 3. 
Vậy hàm số tăng trên các khoảng(- ;-1) và (3;+ ) 
hàm số giảm trên các khoảng(-1;1) và (1;3) 
b) Cực trị : 
Hàm số đạt cực đại tại x=-1 và y CĐ =y(-1)=5 
Hàm số đạt cực tiểu tại x=3 và y CT =y(3)=3 
c) Giới hạn: 
Vậy đường thẳng: x = 1 là tiệm cận đứng. 
Đường thẳng y = x -2 là tiệm 
Cận xiên 
d)Bảng biến thiên: 
x - -1 1 3 + 
Y’ + 0 - - 0 + 
y 
- 
-5 
- 
+ 
3 
+ 
3) Đồ thị: Đồ thị cắt trục tung tại (0;-6) , đồ thị không cắt 
trục hoành 
Gọi I(1;-1) là giao điểm hai tiệm cận. Tịnh tiến hệ trục 
toạ độ theo véc tơ OI,ta có: 
Hàm số lẻ trên R\{0} ,vậy I là tâm đối xứng của đồ thị 
y= x-2 
x=1 
x 
y 
y 
hamhuuti.gsp 
Ví dụ 2) Khảo sát hàm số: 
1)Tập xác định : R \{-2} 
2) Sự biến thiên: 
a) Chiều biến thiên 
y’=-2-3/(x+2) 2 <0 x -2,hàm số nghịch biến trên 
hai khoảng (- ; -2) và (-2; + ) 
b) Cực trị: h àm số không có cực trị 
c) Giới hạn: 
Đường thẳng : x= -2 là tiệm cận đứng 
Đường thẳng y=-2x+1 là tiệm cận xiên 
d) Bảng biến thiên 
 x - -2 + 
y’ - - 
y 
+ 
- 
+ 
- 
Tóm tắt: 
Nếu ACa’>0 hàm số có cực trị 
Nếu ACa’<0 hàm số đơn điệu trên hai khoảng xác 
định. 
Nếu C = 0 hàm số trở thành y =Ax+B ,x -b’/a’ 
Tiệm cận đứng: x= -b’/a’ 
Tiệm cận xiên: y =Ax+B 
Giao điểm hai tiệm cận là tâm đối xứng 
Đồ thị có các dạng sau: 
Hàm số 
giảm 
Hàm số 
tăng 
Hàm số 
Có CĐ 
CT 
Hàm số 
Có CĐ 
CT 
Bài tập: 
Bài tập SGK 
2) Các bài tập ôn tập chương 
3) Chứng minh rằng đồ thị hàm số: 
 và ax 2 +bx+c không chia hết cho 
a’x+b’ 
Có một tâm đối xứng và hai trục đối xứng