Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 4: Đường tiệm cận

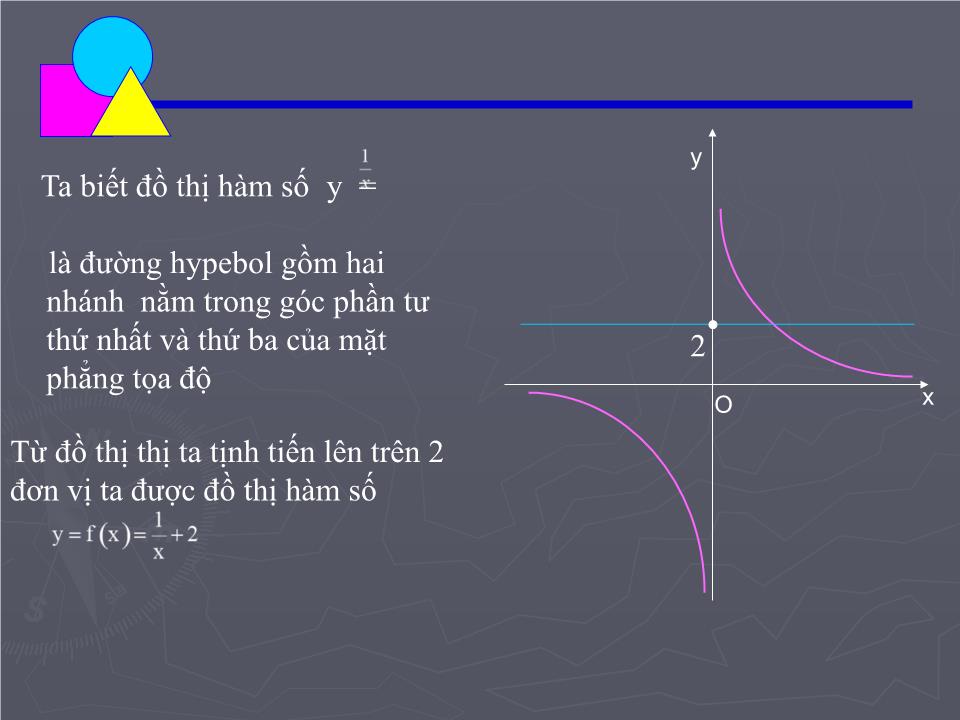
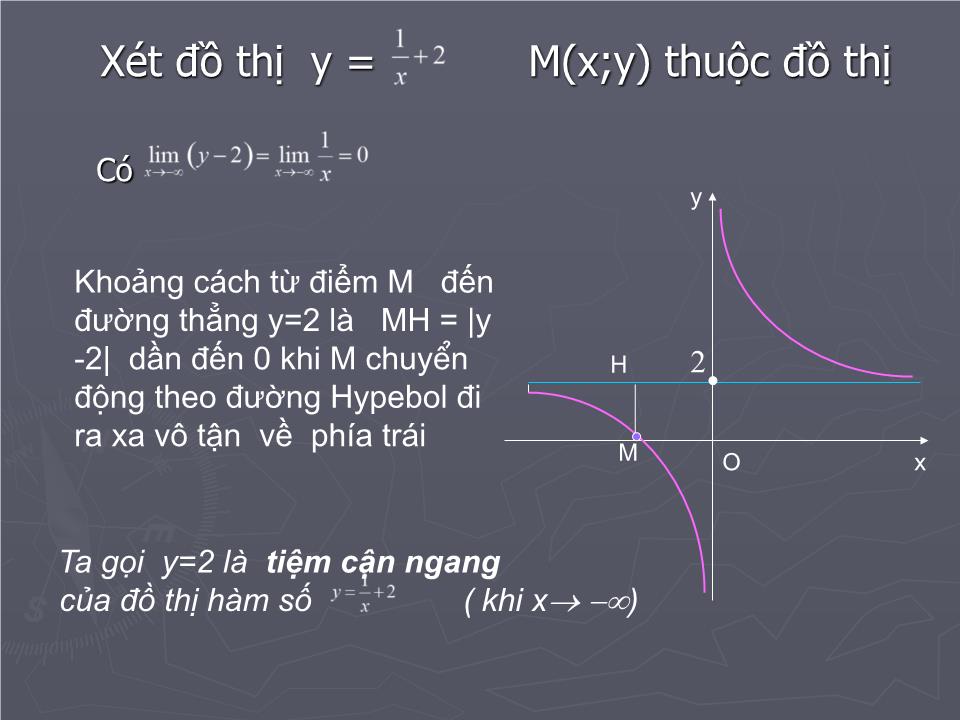
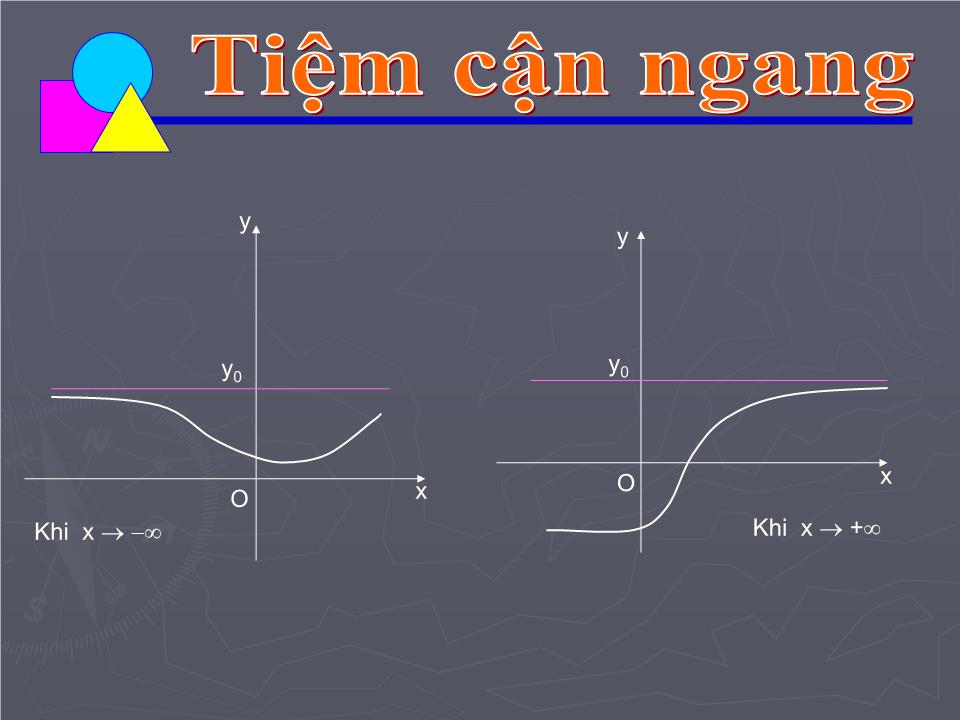
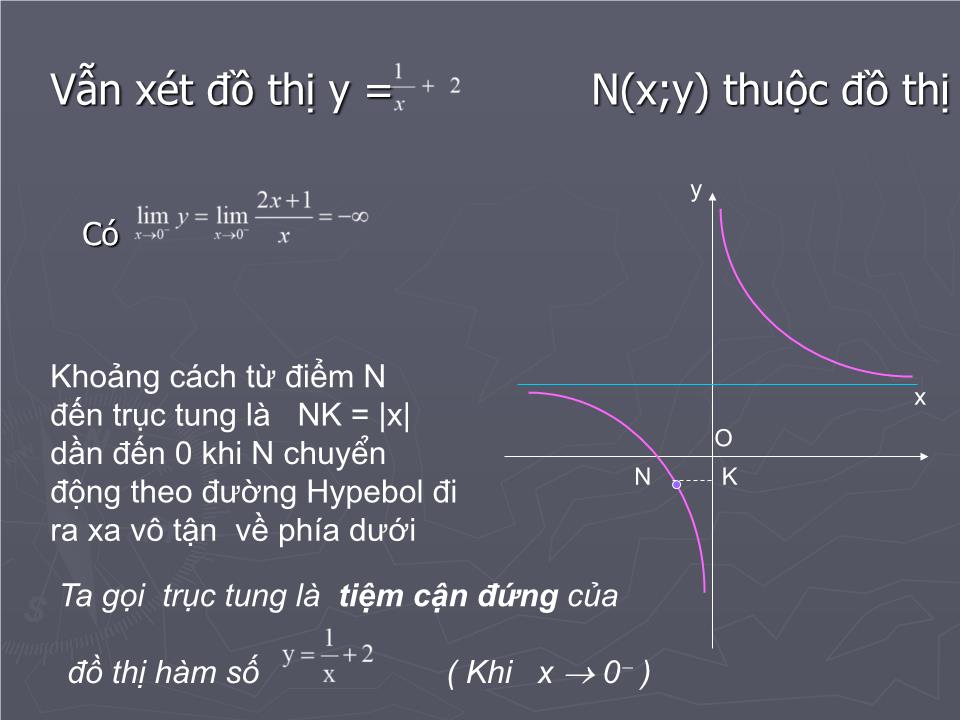
TRƯỜNG THPT CHUYÊN NGUYỄN DU 
Đường tiệm cận 
BÀI 4 
Người dạy: Nguyễn Văn Quang 
KIỂM TRA BÀI CŨ 
Tính các giới hạn sau 
Ta biết đồ thị hàm số y = 
 là đường hypebol gồm hai nhánh nằm trong góc phần tư thứ nhất và thứ ba của mặt phẳng tọa độ 
O 
y 
x 
Từ đồ thị thị ta tịnh tiến lên trên 2 đơn vị ta được đồ thị hàm số 
2 
Xét đồ thị y = M(x;y) thuộc đồ thị  
 Có 
Khoảng cách từ điểm M đến đường thẳng y=2 là MH = |y-2| dần đến 0 khi M chuyÓn ®éng theo đường Hypebol đi ra xa vô tận về phía trái 
 Ta gọi y=2 là tiệm cận ngang 
 của đồ thị hàm số ( khi x ) 
M 
H 
O 
x 
y 
2 
Xét đồ thị y = M(x;y) thuộc đồ thị . 
Có 
Khoảng cách từ điểm M đến trục hoành là MH = |y-2| dần đến 0 khi M chuyÓn ®éng theo đường Hypebol đi ra xa vô tận về phía phải 
O 
M 
H 
x 
y 
Ta gọi đường thẳng y=2 là tiệm cận ngang 
của đồ thị hàm số ( khi x + ) 
 1. Đường tiệm cận ngang 
ĐƯỜNG TIỆM CẬN 
Định nghĩa 1: 
Đường thẳng y = y 0 gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu một trong hai điều kiện sau được thỏa mãn 
Khi x + 
O 
y 
x 
y 0 
Khi x 
O 
y 
y 0 
x 
Tiệm cận ngang 
Em hãy phát biểu định nghĩa đ ư ờng tiệm cận ngang của đồ thị hàm số 
Mỗi nhóm vận dụng định nghĩa tìm tiệm cận ngang của đồ thị mỗi hàm số sau 
 KQ: TCN y =1/3 
 KQ: TCN y = 0 
 KQ: Không có TCN 
Củng cố khái niệm TCN 
Ví dụ 1: 
Qua các ví dụ vừa xét và dựa vào kiến thức về giới hạn có dạng em hãy cho nhận xét về dấu hiệu nhận biết một hàm phân thức hữu tỉ có tiệm cận ngang? 
Hàm phân thức hữu tỉ (không suy biến) có tiệm cận ngang khi bậc của tử số nhỏ h ơ n hoặc bằng bậc của mẫu số 
Em hãy cho một ví dụ về hàm số và tìm tiệm cận ngang của hàm số vừa chỉ ra. 
Củng cố khái niệm TCN 
Có 
Vẫn xét đồ thị y = N(x;y) thuộc đồ thị . 
Khoảng cách từ điểm N đến trục tung là NK = |x| dần đến 0 khi N chuyÓn ®éng theo đường Hypebol đi ra xa vô tận về phía dưới 
N 
K 
O 
y 
x 
Ta gọi trục tung là tiệm cận đứng của 
 đồ thị hàm số ( Khi x 0 ) 
Vẫn xét đồ thị y = N(x;y) thuộc đồ thị . 
Có 
Khoảng cách từ điểm N đến trục tung là NK = |x| dần đến 0 khi N chuyÓn ®éng theo đường Hypebol đi ra xa vô tận về phía trên 
N 
K 
y 
x 
O 
Ta gọi trục tung là tiệm cận đứng của 
 đồ thị hàm số ( Khi x 0 + ) 
Định nghĩa 2: 
 Đường thẳng x = x 0 gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu một trong các điều kiện sau được thỏa mãn 
ĐƯỜNG TIỆM CẬN 
 2 . Đường tiệm cận ngang 
. 
. 
O 
O 
y 
O 
O 
x 
x 
x 
x 
y 
y 
y 
x 0 
x 0 
x 0 
x 0 
Em hãy phát biểu định nghĩa đ ư ờng tiệm cận đứng của đồ thị hàm số 
Mỗi nhóm vận dụng định nghĩa tìm tiệm cận đứng của đồ thị mỗi hàm số sau 
 KQ: TCĐ x = -1 
 KQ: có 2 TCĐ x = -1 và x = 2 
 KQ: Không có TCĐ 
 KQ: Không có TCĐ 
CỦNG CỐ KHÁI NIỆM TIỆM CẬN ĐỨNG 
Qua các ví dụ vừa xét và dựa vào kiến thức đã học về giới hạn em hãy cho nhận xét về dấu hiệu nhận biết một hàm phân thức hữu tỉ có tiệm cận đứng? 
Hàm phân thức hữu tỉ (không suy biến) có tiệm cận đứng khi mẫu số có nghiệm và mọi nghiệm của mẫu số không đồng thời là nghiệm của tử số 
Em hãy cho một ví dụ về hàm số và tìm tiệm cận đứng của hàm số vừa chỉ ra. 
CỦNG CỐ KHÁI NIỆM TIỆM CẬN ĐỨNG 
Bài tập 1 : Cho hàm số 
H ư ớng dẫn: 
Ph ươ ng án đúng là C) 
TCN : Là đường thẳng y = 2 
 (khi x và khi x + ) 
TCĐ : Là đường thẳng x = 2 
(khi x ( 2) + và khi x ( 2) ) 
2 
-2 
O 
x 
y 
Số đ ư ờng tiệm cận ( TCĐ hoặc TCN) của đồ thị hàm số đã cho là: A) 0; B) 1; C) 2; D) 3. 
Bài tập 2 : Cho hàm số 
H ư ớng dẫn: 
Ph ươ ng án đúng là D) 
TCN: Là đường thẳng y = 1 
 ( khi x + ) 
 Là đường thẳng y = 1 
 ( khi x ) 
 TCĐ: Là đường thẳng x = 0 
 ( Khi x 0 và khi x 0+ ) 
Số đ ư ờng tiệm cận ( TCĐ hoặc TCN) của đồ thị hàm số đã cho là: A) 0; B) 1; C) 2; D) 3. 
O 
1 
-1 
y 
x 
 Em hãy cho biết các nội dung chính đã học trong bài hôm nay? 
 Hãy nêu cách tìm đ ư ờng tiệm cận ngang của đồ thị hàm số 
 Hãy nếu cách tìm đ ư ờng tiệm cận đứng của đồ thị hàm số 
CỦNG CỐ BÀI HỌC 
Qua bài học hôm này các em cần nắm đ ư ợc : 
1. Về kiến thức: 
Hiểu đ ư ợc định nghĩa đ ư ờng tiệm cận ngang, đ ư ờng tiệm cận đứng của đồ thị hàm số 
Hiểu đ ư ợc cách tìm đ ư ờng tiệm cận ngang, đ ư ờng tiệm cận đứng của đồ thị hàm số 
2. Về kĩ năng : 
Biết cách tìm tiệm cận ngang, tiệm cận đứng của đồ thị hàm số nói chung, hàm phân thức hữu tỉ nói riêng 
Nhận biết đ ư ợc một hàm phân thức hữu tỉ có đ ư ờng tiệm cận ngang, đ ư ờng tiệm cận đứng 
3. Về t ư duy và thái độ : 
Hiểu đ ư ợc sự tiệm cận của một đ ư ờng thẳng với một đ ư ờng cong, chính là sự xích lại gần nhau về khoảng cách giữa chúng 
Chủ động phát hiện, chiếm lĩnh tri thức mới. Biết quy lạ về quen. 
4. Vận dụng làm các bài tập số : 1 và 2 trang 33 SGK. 
HƯỚNG DẪN VỀ NHÀ