Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 3: Giá trị lớn nhất. Giá trị nhỏ nhất của hàm số
Cho hàm số y = f(x) xác định trên tập D
Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D ,
nếu f(x) ≤ M với mọi x thuộc D và tồn tại x0 D sao cho f(x0) = M
kí hiệu : M = max f(x)
Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D ,
nếu f(x) ≥ M với mọi x thuộc D và tồn tại x0 D sao cho f(x0) = m
kí hiệu : m = min f(x)
Chú ý :
Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó . Ví dụ :
Không có giá trị lớn nhất và nhỏ nhất trên khoảng ( 0 ; 1)
Tuy nhiên cũng có những hàm số có giá trị lớn nhất và giá trị nhỏ nhất trên 1 khoảng như ví dụ sau :
Ví dụ 3 .
Cho tấm tôn nhôm hình vuông cạnh a . Người ta cắt ở 4 góc 4 hình vuông bằng nhau , rồi gấp tấm nhôm như hình vẽ để được cái hộp không nắp . Tính cạnh của các hình vuông bị cắt sao cho thể tích của khối hộp là lớn nhất .

Trang 1

Trang 2

Trang 3
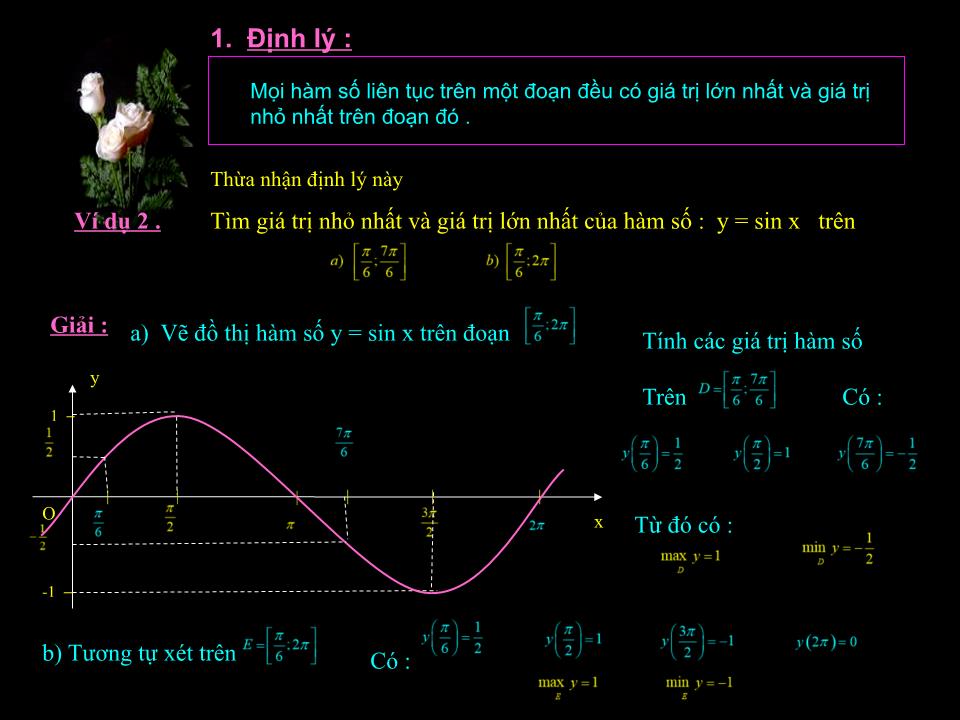
Trang 4
Trang 5

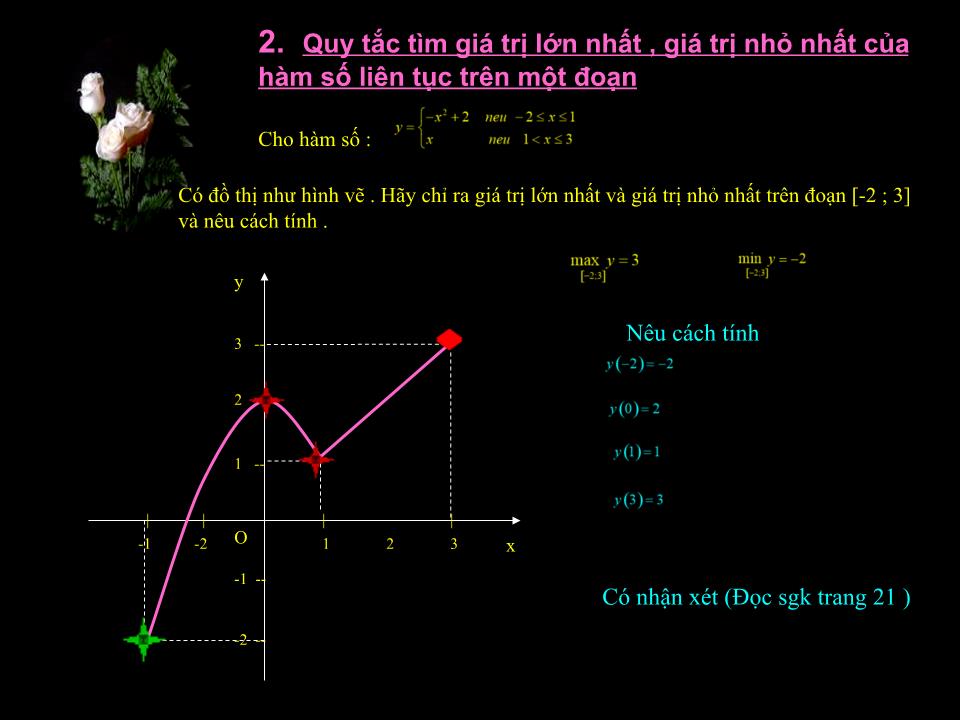
Trang 6

Trang 7
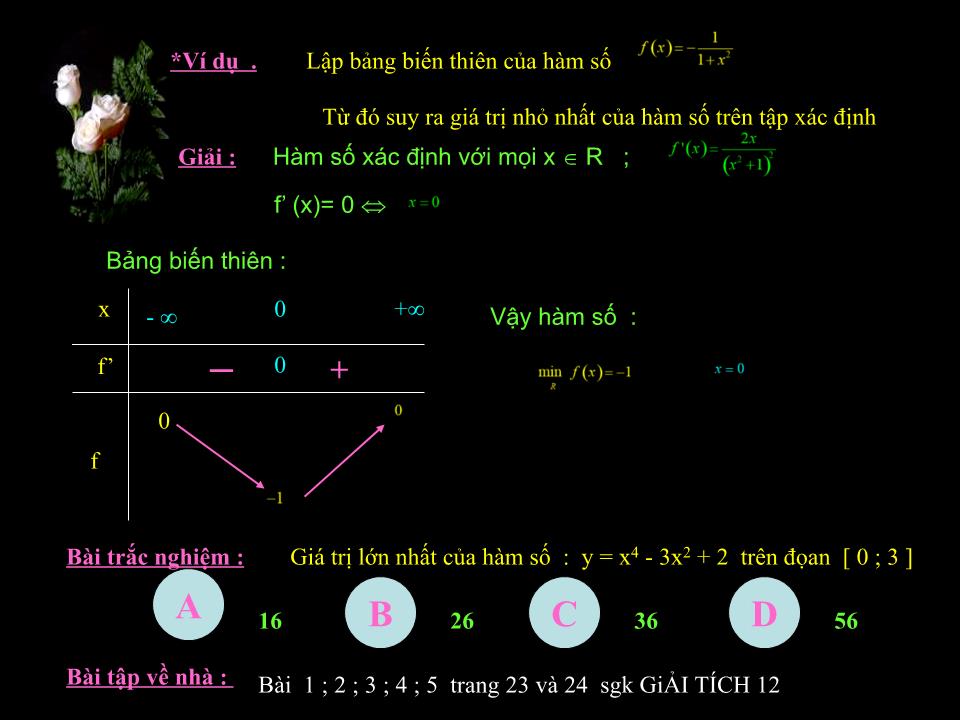
Trang 8

Trang 9
Tóm tắt nội dung tài liệu: Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 3: Giá trị lớn nhất. Giá trị nhỏ nhất của hàm số

Giải tích 12 Bài 3 : Giá trị lớn nhất Giá trị nhỏ nhất CỦA HÀM SỐ Giáo viên : Phạm Quốc Khánh Chương trình thay sách Toán THPT của Bộ GD-ĐT I - ĐỊNH NGHĨA Cho hàm số y = f(x) xác định trên tập D Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D , nếu f(x) ≤ M với mọi x thuộc D và tồn tại x 0 D sao cho f(x 0 ) = M kí hiệu : M = max f(x) D b) Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D , nếu f(x) ≥ M với mọi x thuộc D và tồn tại x 0 D sao cho f(x 0 ) = m kí hiệu : m = min f(x) D Ví dụ 1 . Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số : trên khoảng ( 0 ; + ∞) Giải : Trên (0 ; + ∞) có : Bảng biến thiên : x 0 1 + ∞ y’ y + 0 + ∞ -1 + ∞ Từ bảng biến thiên trên khoảng (0 ; + ∞) hàm số có giá trị cực tiểu duy nhất đó cũng là giá trị nhỏ nhất của hàm số Vậy min f(x) = - 3 ( tại x = 1) (0 ; + ∞) Không tồn tại giá trị lớn nhất của hàm số trên (0 ; + ∞) II - CÁCH TÍNH GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN Đặt vấn đề : Xét tính đồng biến , nghịch niến và Tính giá trị nhỏ nhất , giá trị lớn nhất của hàm số : a) y = x 2 trên [-3 ; 0] b) trên [3 ; 5] a) y = x 2 trên [-3 ; 0] Giải : Trên [-3 ; 0] ) có : y’ = 2x và y’ = 0 x = 0 Bảng biến thiên : x -3 0 y’ y 0 9 0 trên [3 ; 5] Trên [3 ; 5] ) có : y’ = y’ < 0 Bảng biến thiên : x 3 5 y’ y 2 3/2 1. Định lý : Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó . Thừa nhận định lý này Ví dụ 2 . Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số : y = sin x trên Giải : a) Vẽ đồ thị hàm số y = sin x trên đoạn O x y | | | | | 1 -1 | Tính các giá trị hàm số Trên Có : Từ đó có : b) Tương tự xét trên Có : 2. Quy tắc tìm giá trị lớn nhất , giá trị nhỏ nhất của hàm số liên tục trên một đoạn Cho hàm số : Có đồ thị như hình vẽ . Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-2 ; 3] và nêu cách tính . O x y | | | -2 -- | -1 -2 1 2 3 -1 -- 1 -- 2 -- 3 -- Nêu cách tính Có nhận xét (Đọc sgk trang 21 ) QUY TẮC : 1) Tìm các điểm x 1 ; x 2 ; x j trên khoảng (a ; b) tại đó f’(x) = 0 hoặc f’(x) không xác định 2) Tìm f(a) ; f(x 1 ) ; f(x 2 ) ; ; f(x j ) ; f(b) 3) Tìm số lớn nhất M ; số nhò nhất m các số trên và có Chú ý : Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó . Ví dụ : Không có giá trị lớn nhất và nhỏ nhất trên khoảng ( 0 ; 1) Tuy nhiên cũng có những hàm số có giá trị lớn nhất và giá trị nhỏ nhất trên 1 khoảng như ví dụ sau : Ví dụ 3 . Cho tấm tôn nhôm hình vuông cạnh a . Người ta cắt ở 4 góc 4 hình vuông bằng nhau , rồi gấp tấm nhôm như hình vẽ để được cái hộp không nắp . Tính cạnh của các hình vuông bị cắt sao cho thể tích của khối hộp là lớn nhất . a Giải : Gọi x là độ dài cạnh của hình vuông bị cắt bỏ Thể tích kh ố i hộp là : Ta phải tìm x 0 sao cho V(x 0 ) có giá trị lớn nhất . Có V’(x) = (a-2x)(a-6x) và trên ; V’(x) = 0 Bảng biến thiên : x 0 V’(x) V(x) 0 + ─ 0 0 Hàm số có 1 điểm cực trị duy nhất nên tại đó V(x) có giá trị lớn nhất . *Ví dụ . Lập bảng biến thiên của hàm số Giải : Hàm số xác định với mọi x R ; f’ (x)= 0 Bảng biến thiên : x - ∞ f’ f 0 + ∞ 0 ─ 0 Vậy hàm số : + Bài trắc nghiệm : Giá trị lớn nhất của hàm số : y = x 4 - 3x 2 + 2 trên đọan [ 0 ; 3 ] A 16 B 26 C 36 D 56 Bài tập về nhà : Bài 1 ; 2 ; 3 ; 4 ; 5 trang 23 và 24 sgk GiẢI TÍCH 12 Từ đó suy ra giá trị nhỏ nhất của hàm số trên tập xác định Kính chúc thầy cô và các em khỏe Hẹn ngày gặp lại
File đính kèm:
 bai_giang_dai_so_lop_12_chuong_1_cuc_tri_cua_ham_so_bai_3_gi.ppt
bai_giang_dai_so_lop_12_chuong_1_cuc_tri_cua_ham_so_bai_3_gi.ppt

