Bài giảng Đại số Lớp 12 - Chương 1: Cực trị của hàm số - Bài 2: Cực trị của hàm số

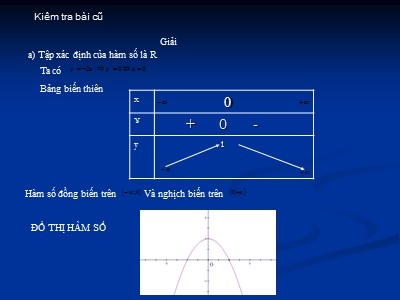
 Giải 
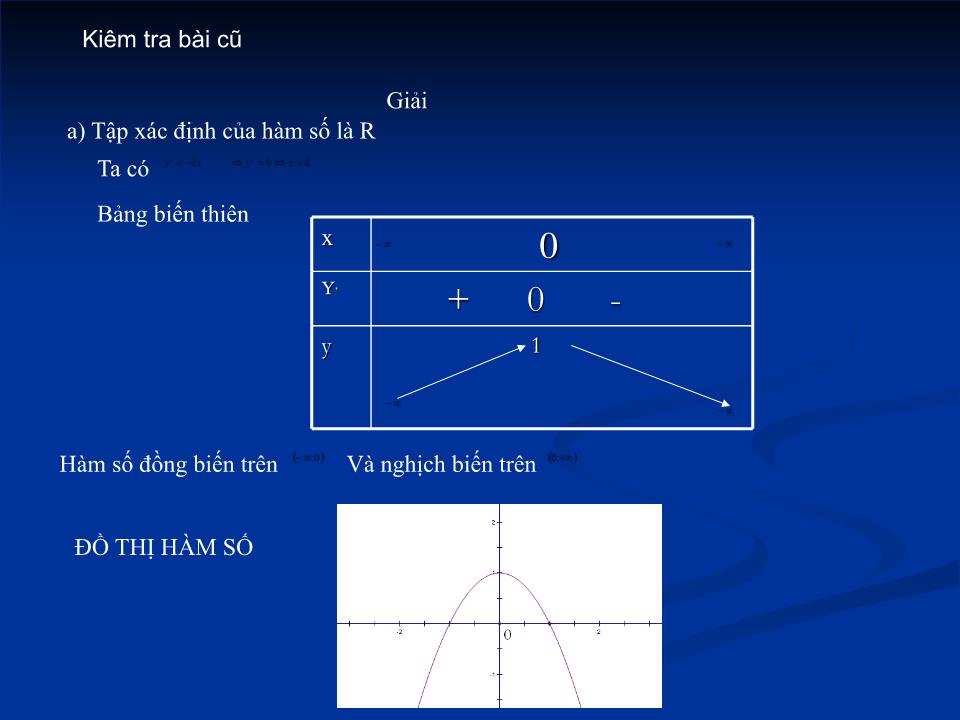
a) Tập xác định của hàm số là R 
Ta có 
Bảng biến thiên 
x 
 0 
Y , 
 + 0 - 
y 
 1 
ĐỒ THỊ HÀM SỐ 
Hàm số đồng biến trên 
Và nghịch biến trên 
Kiêm tra bài cũ 
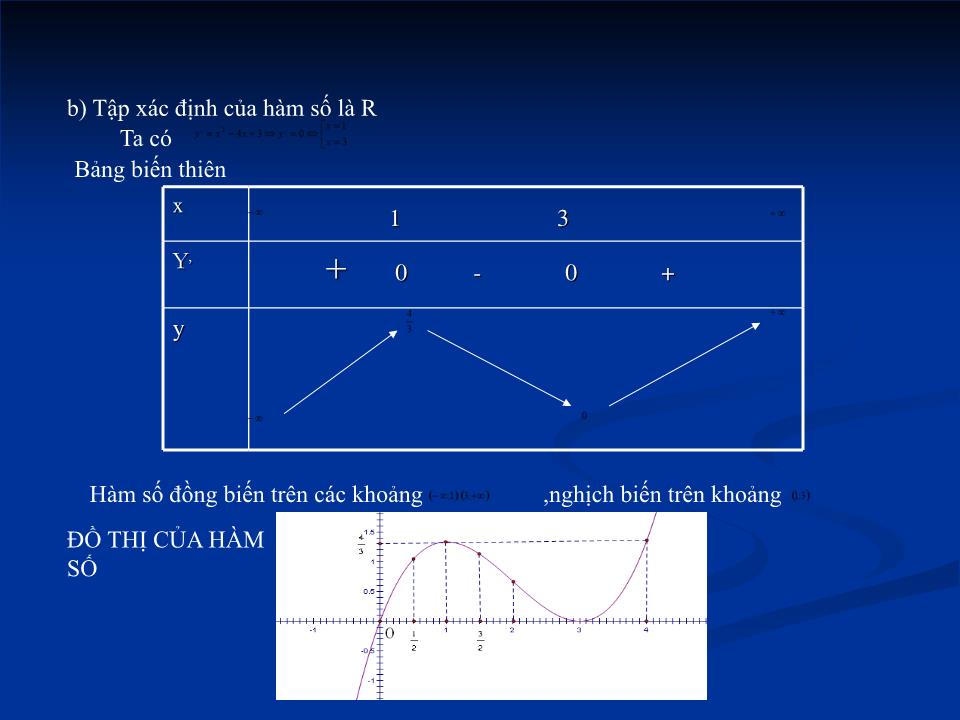
b) Tập xác định của hàm số là R 
Ta có 
Bảng biến thiên 
x 
 1 3 
Y , 
 + 0 - 0 + 
y 
Hàm số đồng biến trên các khoảng 
,nghịch biến trên khoảng 
ĐỒ THỊ CỦA HÀM SỐ 
Tiết 4. Bài 2 Cực trị của hàm số 
I- khái niệm cực đại , cực tiểu 
ĐỊNH NGHĨA : CHO HÀM SỐ Y=F(X) XÁC ĐỊNH VÀ LIÊN TỤC TRÊN KHOẢNG (A;B) VÀ ĐIỂM 
a) Nếu 
đạt cực đại tại x 0 
b) Nếu 
đạt cực tiểu tại x 0 
Chú ý 
1.Nếu hàm số f(x) đạt cực đại (cực tiểu ) tại x 0 thì x 0 đ ư ợc gọi là điểm cực đại ( điểm cực tiểu ) của hàm số. 
 f(x 0 ) đ ư ợc gọi là giá trị cực đại ( giá trị cực tiểu ) của hàm số, kí hiệu là f CĐ (f CT ), còn điểm M(x 0 ;f(x 0 )) đ ư ợc gọi là điểm cực đại ( điểm cực tiểu ) của hàm số. 
2.Các điểm cực đại và cực tiểu đ ư ợc gọi chung là điểm cực trị.Giá trị cực đại (giá trị cực tiểu ) cồn gọi là cực đại ( cực tiểu ) và đ ư ợc gọi chung là cực trị của hàm số. 
3.Dễ dàng chứng minh đ ư ợc rằng, nếu hàm số y=f(x) có đạo hàm trên khoảng (a;b) và đạt cực đại hoặc cực tiểu tại x 0 thì f ’ (x 0 )= 0. 
II.Điều kiện đủ để hàm số có cực trị. 
Định lí 1 
Giả sử hàm số y=f(x) liên tục trên khoảng K=(x 0 -h;x 0 +h) và có đạo hàm trên K hoặc trên K\{x 0 }, với h>0. 
a) Nếu f ’ (x) > 0 trên khoảng ( x 0 -h;x 0 ) và f ’ (x) < 0 trên khoảng ( x 0 ;x 0 +h) thì x 0 là một điểm cực đại của hàm số f(x). 
b) Nếu f ’ (x) 0 trên khoảng (x 0 ;x 0 +h) thì x 0 là một điểm cực tiểu của hàm số f(x). 
x 
X 0 -h x 0 x 0 +h 
f ’ (x) 
 + - 
f(x) 
 f C§ 
x 
X 0 -h x 0 x 0 +h 
f ’ (x) 
 - + 
 f(x) 
 f CT 
ví dụ 1. Tìm các điểm cực trị của hàm số f(x) = -x 2 +1 
ví dụ 2. Tìm các điểm cực trị của hàm số y = x 3 – x 2 – x + 3 
ví dụ 3. Tìm cực trị của hàm số 
Tìm tập xác định của các hàm số trên,tìm đạo hàm bậc nhất ,tìm các điểm f ’ (x) = 0 hoặc f ’ (x) không xác định,lập bảng biến thiên và từ đó suy ra các điểm cực trị của các hàm số đó? 
III – Quy tắc tìm cục trị 
 Quy tắc I. 
1.Tìm tập xác định. 
2.Tìm f ’ (x).Tìm các điểm tại đó f ’ (x) bằng 0 hoặc f ’ (x) không xác định. 
3.Lập bảng biến thiên. 
4.Từ bảng biến thiên suy ra các điểm cực trị. 
H5. hãy tìm các điểm cực trị của hàm số f(x)= x(x 2 – 3) 
ĐỊNH LÍ 2 
GIẢ SỬ HÀM SỐ Y=F(X) CÓ ĐẠO HÀM CẤP HAI TRONG KHOẢNG (X 0 -H ; X 0 +H), VỚI H > 0.KHI ĐÓ: 
NẾU F ’ (X 0 ) = 0, F ’’ (X 0 ) > 0 THÌ X 0 LÀ ĐIỂM CỰC TIỂU. 
NẾU F ’ (X 0 ) = 0, F ’’ (X 0 ) < 0 THÌ X 0 LÀ ĐIỂM CỰC ĐẠI. 
Quy tắc II 
1.Tìm tập xác định. 
2.Tính f ’ (x). Giải ph ươ ng trình f ’ (x)= 0 và kí hiệu x i ( i= 1,2,) là các nghiệm của nó. 
3.Tính f ’’ (x) và f ’’ (x i ). 
4.Dựa vào dấu của f ’’ (x i ) suy ra tính chất cực trị của điểm x i . 
Ví dụ 4.Tìm cực trị của hàm số 
ví dụ 5.Tìm cấc điểm cực trị của hàm số f(x) = sin2x