Applying inverse method for heat transfer of high speed spindle
When working under high speed, friction
of bearings (and power loss of motorized) in the
spindle will generate heat which leads to increase
temperature and further cause thermal deformation
in the spindle. Therefore,understanding temperature
distribution in the spindle can give useful
information for predicting and controlling thermal
error. To estimatetemperature fieldin the spindle,
the heat sources are indispensable. Palmgren[1]
gave an empirical formula to estimate total bearing
friction torque that was then used for calculating
bearing heat generation. By adding the spinning
friction moments to formula, Harris presented a
new form for calculating heat generation of bearing
in [2]. Palmgren’s model has achieved popular
acceptance as an accurate method. Bossmanns and
Tu [3] proposed a model to determine quantitative
heat source of the built-in motor and the bearings.
Based on data from coast test, they established
empirical equations which are function of preload
and rotational speed for calculating bearing heat
generated. Moorthy[4] introduced an improved
analytical model for estimation of heat generation
in angular contact ball bearings of high speed
spindle. Through literature review, it can be
seen that none of researches were investigated to
obtain heat generated in bearings by using inverse
heat transfer method. Recently, inverse method
for estimating heat generation and interface
temperature in ultrasonic welding [12, 13] and
temperature-dependent thermophysical properties
of material [14] was successfully studied.In this
study, an inverse method is proposed to predict heat
sources (heat generated by bearings)in the spindle.
A combination of Mechanical Ansys Parametric
Design Language (MAPDL) and Conjugate
GradientMethod (CGM) is applied to find the
unknown heat sources.

Trang 1

Trang 2
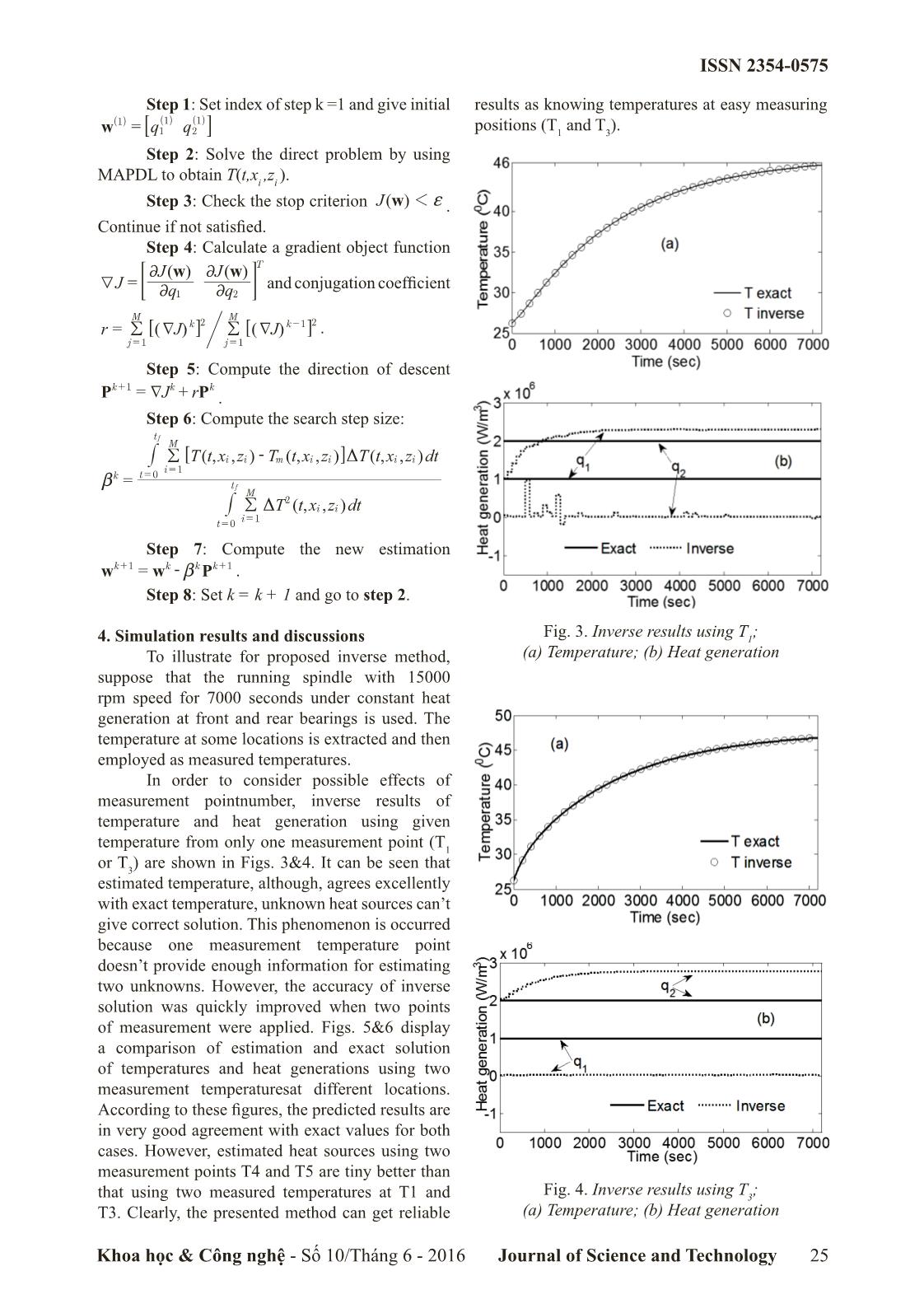
Trang 3
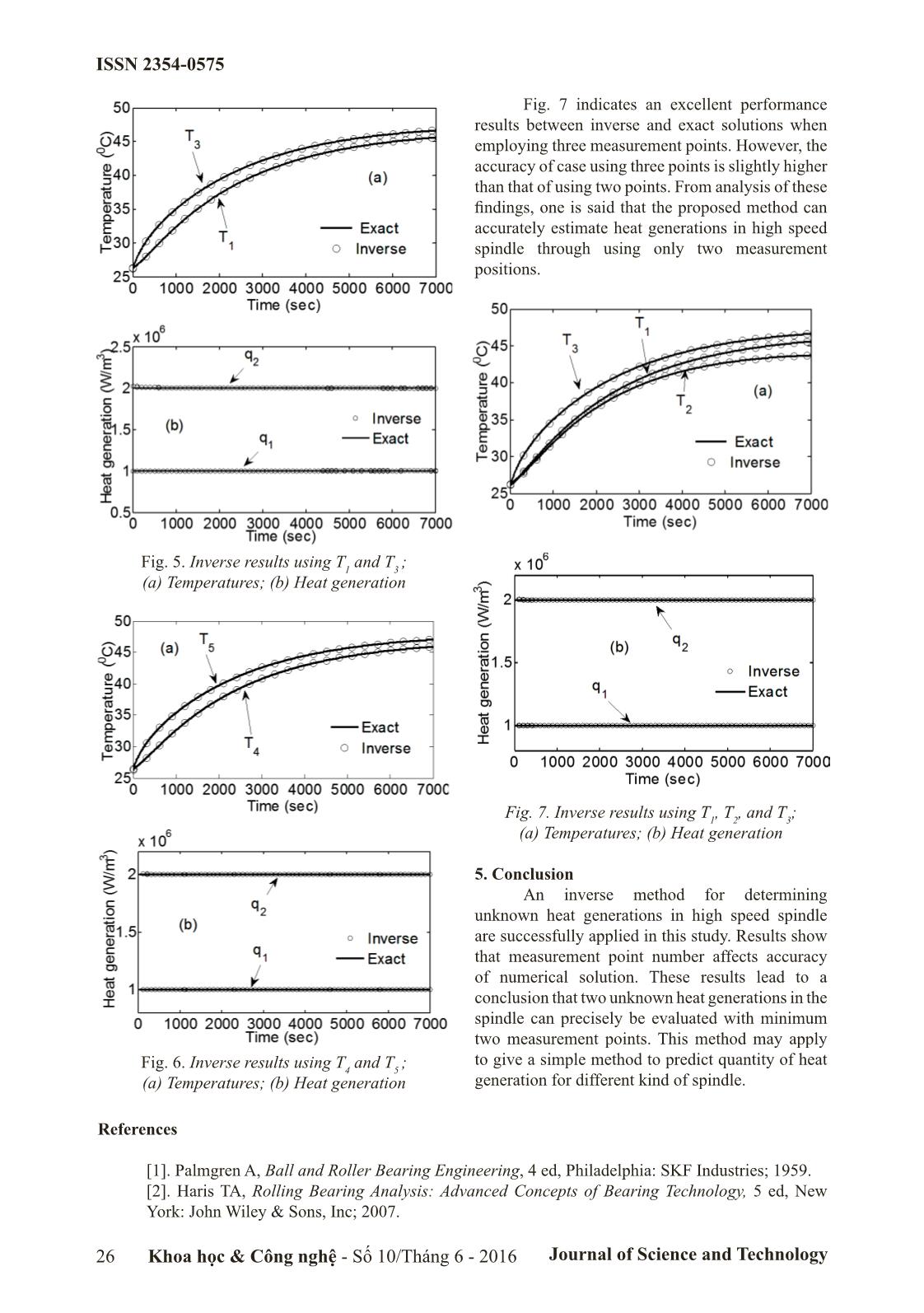
Trang 4

Trang 5
Tóm tắt nội dung tài liệu: Applying inverse method for heat transfer of high speed spindle

ISSN 2354-0575 APPLYING INVERSE METHOD FOR HEAT TRANSFER OF HIGH SPEED SPINDLE Than Van The1, Ngo Thi Thao2 1 Feng Chia University 2 Hung Yen University of Technology and Education Received: 15/4/2016 Revised: 02/6/2016 Accepted for publication: 10/6/2016 Abstract: This paper presents an inverse method for finding quantity of heat sources in high speed spindle. A commercial ANSYS software and Conjugate Gradient optimization method are used to construct the proposed inverse method. Simulations for different number of measurementpoints andlocations are performed. These results show that excellent estimation on heat generation can be obtained through using only two measurement points. The current methodology will provide a useful tool to investigate the complex heat transfer process in the high speed spindle. Keywords: Inverse method, High speed spindle,Conjugate Gradient Method, ANSYS Software. 1. Introduction obtain heat generated in bearings by using inverse When working under high speed, friction heat transfer method. Recently, inverse method of bearings (and power loss of motorized) in the for estimating heat generation and interface spindle will generate heat which leads to increase temperature in ultrasonic welding [12, 13] and temperature and further cause thermal deformation temperature-dependent thermophysical properties in the spindle. Therefore,understanding temperature of material [14] was successfully studied.In this distribution in the spindle can give useful study, an inverse method is proposed to predict heat information for predicting and controlling thermal sources (heat generated by bearings)in the spindle. error. To estimatetemperature fieldin the spindle, A combination of Mechanical Ansys Parametric the heat sources are indispensable. Palmgren[1] Design Language (MAPDL) and Conjugate gave an empirical formula to estimate total bearing GradientMethod (CGM) is applied to find the friction torque that was then used for calculating unknown heat sources. bearing heat generation. By adding the spinning friction moments to formula, Harris presented a 2. Thermal model of the high speed spindle new form for calculating heat generation of bearing 2.1 The high speed spindle structure in [2]. Palmgren’s model has achieved popular A direct driver spindle with 24000 rpm acceptance as an accurate method. Bossmanns and maximum speed, namely, TD30 is investigated in Tu [3] proposed a model to determine quantitative this study. To design the complex spindle, CATIA heat source of the built-in motor and the bearings. software is used to draw the spindle as shown in Based on data from coast test, they established Fig. 1. To simplify the spindle model, small nuts, empirical equations which are function of preload holes, and small structures are omitted. Material and rotational speed for calculating bearing heat properties of each part in the spindle are listed generated. Moorthy[4] introduced an improved in Table 1. A finite element (FE) model of the analytical model for estimation of heat generation spindle is established in MAPDL. Because of the in angular contact ball bearings of high speed symmetric spindle, a small partition of the spindle spindle. Through literature review, it can be (10) is considered instead of entire spindle. Meshed seen that none of researches were investigated to model of the spindle is displayed in Fig.2. Fig. 1. High speed spindle structure Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 23 ISSN 2354-0575 Fig. 2. Meshed model of the spindle in ANSYS Table 1. Material properties includes force and free convection. The convection Shaft Housing Inner/ Balls Other coefficient is defined by Outer parts hN= uakdir (4) Material SCM SCM440 SUJ2 Ce- S45C in which d is the equivalent diameter of the rotation name 415 ramic bodies/cylinder or size of small gap; Nu is the Density 7850 7800 7830 3200 7830 average Nusselt number. Nu is calculated for (kg/m3) different kind of convection as listed in Table2. Thermal 46.6 43 46 30 47 Table 2. Nusselt number for convection boundary conduc- condition tivity Convection Equations for calculating Nu W/(m.K) boundary Specific 460 450 470 850 480 condition heat Free convection 16/ 2 0 . 387RaD kJ/(kg.K) of horizontal Nu =+06. 91/ 6 82/ 7 Expansion 12.5 11.8 12.5 3.0 12.8 cylinder [9] *410+ ./559 Pr 7A^h coefficient Convection 12/ -6 o Nu = 0 .(6366 Re.Pr) (x10 / C) around rotation shaft [10] 2.2. Heat transfer coefficients 0.241 Forced Ta2 The spindle is assembled from many parts, convection in Nu = 0 . 409 cmFg this leads to create a lot of joint between these rotating annuli 4 ##2 7 parts. Hence, the contact heat transfer at joint of [11] forT10 aF/ g 10 spindle parts must be considered. Thermal contact resistance between the balls and outer/inner rings 3. Inverse method is given by [5] Two unknown heat generations, which 1 r 1 r Rbr = Ke,,+ Ke (1) contain heat generation at front and rear bearings, 2rakball 2 2rakring 2 ``jjare regards as: w = qq12 (5) The contact between outer rings and housing 6@ through small air gap, so the thermal contact Solution of an inverse problem is obtained resistance coefficient is determined as [6, 7]: when the object function is minimized with respect hring hTgapr--()inghTr$$a h to each of unknown parameters. The object function Rhr = + (2) kSring kSair has been defined to solve this inverse problem as: tf M Thermal contact conductance of negative 2 JTw = # / (,txii,)zT- mi(,tx,)zdi t (6) i = 1 assembly of inner ring and shaft is computedas[8]: ^h t = 0 6@ ]Z k tan i p 09. 4 ]h = 11. 3 where T(t,x ,z ) is the estimated temperature on ] v ` H j i i ] a k the housing surface at the measured locations ] forplastic deformation ( } $ 1 ] ) determined from the solution of the direct problem [ 09. 4 (3) ] k tan i p 2 by using an updated estimation for the unknown ]h = 15. 5 ] v d E tan i n quantity w. In order to minimize the objective ] a k ] forplastic deformation ()} < 1 function, the CGM is chosen in this study.The \ The heat transfer convection in spindle algorithm of proposed inverse method as follows: 24 Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology ISSN 2354-0575 Step 1: Set index of step k =1 and give initial results as knowing temperatures at easy measuring ()1 ()1 ()1 w = qq1 2 positions (T and T ). 7A 1 3 Step 2: Solve the direct problem by using MAPDL to obtain T(t,xi ,zi ). 1 Step 3: Check the stop criterion J()w f . Continue if not satisfied. Step 4: Calculate a gradient object function 2J()ww2J()T 4J = and conjugation coefficient <F2q122q M M rJ= //()ddk 2 ()J k-1 2 . j = 1 6 @ j = 1 6 @ Step 5: Compute the direction of descent kk+1 k PP= dJr+ . Step 6: Compute the search step size: tf M # / Tt(,xzii,)- Ttmi(,xz,)iiDTt(,xz,)i dt i = 1 k t = 0 6@ b = tf M 2 # / DTt(,xzii,)dt i = 1 t = 0 Step 7: Compute the new estimation wwkk++11= - bkkP . Step 8: Set k = k + 1 and go to step 2. 4. Simulation results and discussions Fig. 3. Inverse results using T1; To illustrate for proposed inverse method, (a) Temperature; (b) Heat generation suppose that the running spindle with 15000 rpm speed for 7000 seconds under constant heat generation at front and rear bearings is used. The temperature at some locations is extracted and then employed as measured temperatures. In order to consider possible effects of measurement pointnumber, inverse results of temperature and heat generation using given temperature from only one measurement point (T1 or T3) are shown in Figs. 3&4. It can be seen that estimated temperature, although, agrees excellently with exact temperature, unknown heat sources can’t give correct solution. This phenomenon is occurred because one measurement temperature point doesn’t provide enough information for estimating two unknowns. However, the accuracy of inverse solution was quickly improved when two points of measurement were applied. Figs. 5&6 display a comparison of estimation and exact solution of temperatures and heat generations using two measurement temperaturesat different locations. According to these figures, the predicted results are in very good agreement with exact values for both cases. However, estimated heat sources using two measurement points T4 and T5 are tiny better than that using two measured temperatures at T1 and Fig. 4. Inverse results using T3; T3. Clearly, the presented method can get reliable (a) Temperature; (b) Heat generation Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 25 ISSN 2354-0575 Fig. 7 indicates an excellent performance results between inverse and exact solutions when employing three measurement points. However, the accuracy of case using three points is slightly higher than that of using two points. From analysis of these findings, one is said that the proposed method can accurately estimate heat generations in high speed spindle through using only two measurement positions. Fig. 5. Inverse results using T1 and T3 ; (a) Temperatures; (b) Heat generation Fig. 7. Inverse results using T1, T2, and T3; (a) Temperatures; (b) Heat generation 5. Conclusion An inverse method for determining unknown heat generations in high speed spindle are successfully applied in this study. Results show that measurement point number affects accuracy of numerical solution. These results lead to a conclusion that two unknown heat generations in the spindle can precisely be evaluated with minimum two measurement points. This method may apply to give a simple method to predict quantity of heat Fig. 6. Inverse results using T4 and T5 ; (a) Temperatures; (b) Heat generation generation for different kind of spindle. References [1]. Palmgren A, Ball and Roller Bearing Engineering, 4 ed, Philadelphia: SKF Industries; 1959. [2]. Haris TA, Rolling Bearing Analysis: Advanced Concepts of Bearing Technology, 5 ed, New York: John Wiley & Sons, Inc; 2007. 26 Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology ISSN 2354-0575 [3]. Bossmanns B, Tu JF, A Power Flow Model for High Speed Motorized Spindles - Heat Generation Characterization, J Manuf Sci E-T Asme, 2001;123:494-505. [4]. Moorthy RS, Raja VP, An Improved Analytical Model for Prediction of Heat Generation in Angular Contact Ball Bearing, Arab J Sci Eng. 2014;39:8111-9. [5]. Nakajima K, Thermal Contact Resistance between Balls and Rings of A Bearing under Axial, Radial, and Combined Loads, Journal of Thermophysics and Heat Transfer, 1995;9: 88-95. [6]. Bossmanns B, Tu JF, A Thermal Model for High Speed Motorized Spindles, Int J Mach Tool Manu. 1999;39:1345-66. [7]. Liu Z, Pan M, Zhang A, Zhao Y, Yang Y, Ma C, Thermal Characteristic Analysis of High-speed Motorized Spindle System based on Thermal Contact Resistance and Thermal-conduction Resistance. The International Journal of Advanced Manufacturing Technology. February 2015;76:1913-26. [8]. Madhusudana CV, Thermal Contact Conductance, Switzerland: Springer International Publishing; 2014. [9]. Bejan A, Convection Heat Transfer, 2 ed, New York: John Wiley & Sons, Inc.; 1995. [10]. Kendoush AA,, An Approximate Solution of the Convective Heat Transfer from An Isothermal Rotating Cylinder, Int J Heat Fluid Fl. 1996;17:439-41. [11]. Childs PRN, Long CA, A Review of Forced Convective Heat Transfer in Stationary and Rotating Annuli, P I Mech Eng C-J Mec. 1996;210:123-34. [12]. Ngo TT, Huang JH, Wang CC, The BFGS Method for Estimating the Interface Temperature and Convection Coefficient in Ultrasonic Welding, International Communication in Heat and Mass Transfer. 2015; 69:66-75,. [13]. Huang JH, Ngo TT, Wang CC, HSDM and BFGS Method for Determining the Heat Generation and Range of Heat Distribution in Ultrasonic Seam Welding Problem, Numerical Heat Transfer, Part B: Fundamental. 2016; 69:48-68. [14]. Ngo TT, Huang JH, Wang CC, Inverse Simulation and Experimental Verification of Temperature-Dependent Thermophysical Properties, International Communication in Heat and Mass Transfer.2016; 71:137-47. ỨNG DỤNG PHƯƠNG PHÁP NGHỊCH TRONG TRUYỀN NHIỆT CỦA TRỤC CHÍNH TỐC ĐỘ CAO Tóm tắt: Bài báo này trình bày một phương pháp nghịch để tìm nguồn nhiệt sinh ra trong trục chính làm việc với tốc độ cao. Phương pháp nghịch đề xuất được xây dựng bằng cách sử dụng phần mềm thương mại ANSYS và phương pháp tối ưu liên hợp Gradient. Các mô phỏng với số điểm đo và vị trí đo khác nhau được thực hiện. Kết quả cho thấy nguồn nhiệt có thể được dự đoán với độ chính xác cao khi chỉ cần sử dụng nhiệt độ đo tại 2 điểm. Phương pháp hiện tại sẽ cung cấp một công cụ hữu ích cho việc nghiên cứu quá trình truyền nhiệt phức tạp trong các trục chính làm việc với tốc độ cao. Từ khóa: Phương pháp nghịch, Trục chính tốc độ cao, Phương pháp liên hợp Gradient, Phần mềm ANSYS. Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 27
File đính kèm:
 applying_inverse_method_for_heat_transfer_of_high_speed_spin.pdf
applying_inverse_method_for_heat_transfer_of_high_speed_spin.pdf

