A comprehensive review on dual approach to the vibration analysis: some dual techniques and application
Oscillation plays an important role in our daily lives and nature. This reflects the fact
that life and nature are extremely diverse sets of motions. Fidlin wrote “Any motion is
deeply connected with one of the most fundamental properties of nature – its ability to
react with oscillations at any internal change or external influence” [1]. In all areas of human activities vibrational systems are increasingly abundant and varied and the study of
those systems is always required. Most phenomena in our world are essentially nonlinear
and described by nonlinear equations. We might simplify nonlinear phenomena as linear ones to make them easier to understand; however, for further investigation nonlinear
phenomena should be treated as nonlinear problems. Thus, the study of nonlinear problems is of crucial importance not only in all areas of physics but also in engineering and
in other disciplines. In particular, it appears that the analysis of vibration based on nonlinear mathematical models requires appropriate methods. Therefore, new methods for
analysis of nonlinear oscillations always cause concern of scientists and technicians. Recently, a dual approach has been proposed to study the response of nonlinear systems [2]
and some dual techniques have been developed, e.g. [3–27], based on the concept of duality. Nature and life always contain dual inclinations. Those are perspectives that are
contradictory, or complementary to each other. Natural phenomena and human activities exhibit often dual characters which reflect two side processes or/and the relative
balance of two opposite sides. For illustration we may say attack – defense in a football
match, one way and return in an excursion, day and night. When a problem is considered it is quite often that one its side is given too much attention while another side is
almost or completely forgotten. This usual approach doesn’t reflect the real essence of
the problem in question and hence doesn’t yield an expected solution in many cases. The
main issue of a dual approach to a scientific problem is to always consider two different
(dual) aspects of the problem. This allows the study to become more harmonious and
reflects the essence of the problem. In the dual approach a dual technique is one that can
introduce two dual perspectives for the same problem in consideration. Let one needs
to investigate a problem. The use of the dual approach to this problem means that one
should introduce a dual technique that can reflect the essence of the problem.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
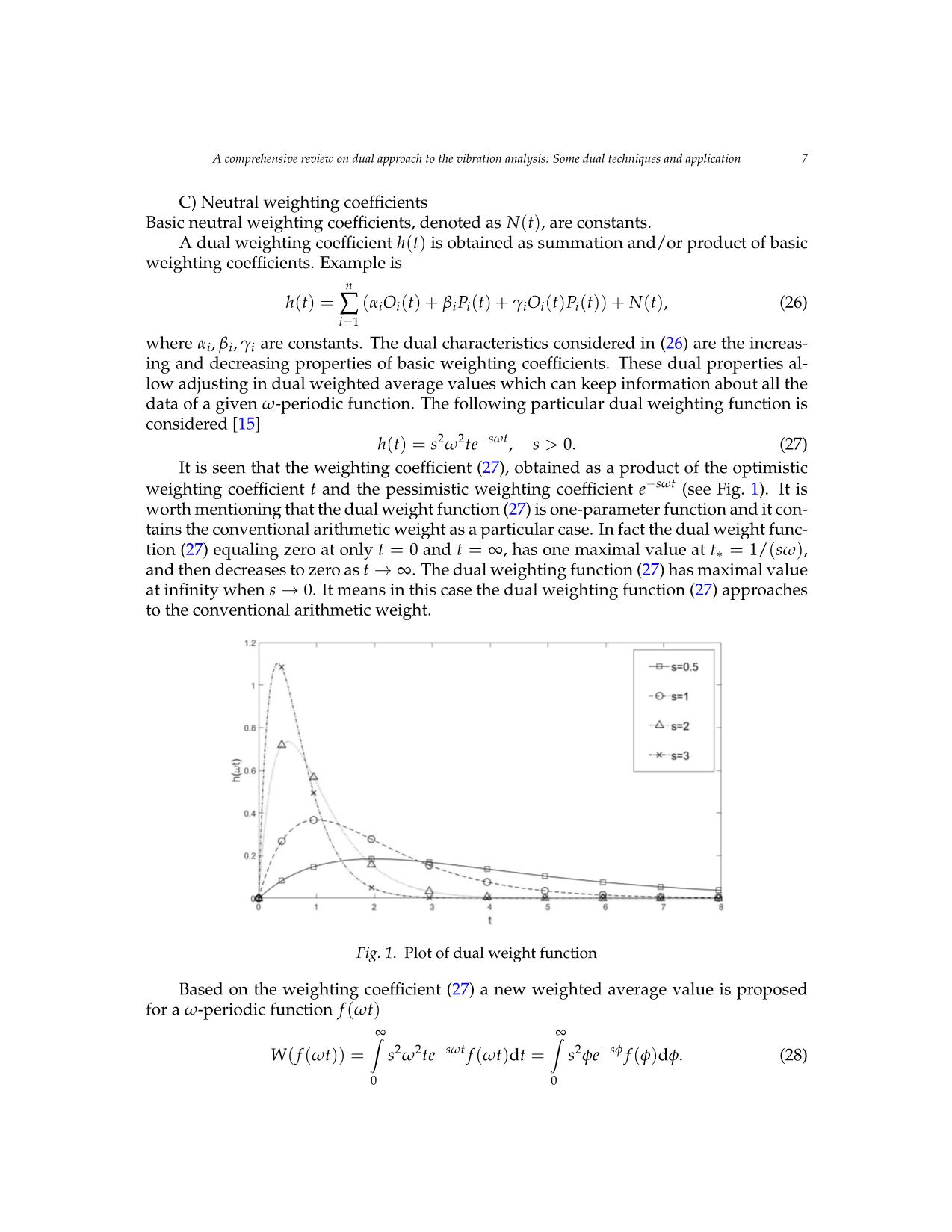
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: A comprehensive review on dual approach to the vibration analysis: some dual techniques and application

Vietnam Journal of Mechanics, VAST, Vol.42, No. 1 (2020), pp. 1 – 14 DOI: https://doi.org/10.15625/0866-7136/14699 A COMPREHENSIVE REVIEW ON DUAL APPROACH TO THE VIBRATION ANALYSIS: SOME DUAL TECHNIQUES AND APPLICATION N. D. Anh1,2 1Institute of Mechanics, VAST, Hanoi, Vietnam 2VNU University of Engineering and Technology, Hanoi, Vietnam E-mail: ndanh@imech.vast.vn Received: 16 October 2019 / Published online: 13 December 2019 Abstract. This paper reviews key ideas of the researches on the dual approach to the vibration analysis. Three types of dual techniques, namely, forward - return dual tech- nique, global-local dual technique, weighted averaging dual technique, for the problem of equivalent replacement are summarized. Different implements and realizations of dual techniques to nonlinear vibration analysis and design of dynamic absorbers are reviewed. Finally, the challenging issues based on the dual techniques are discussed. A number of possibilities for developing analytical techniques related to dual techniques are proposed. Keywords: dual approach, dual technique, forward - return dual, global-local dual, weighted averaging dual. 1. INTRODUCTION Oscillation plays an important role in our daily lives and nature. This reflects the fact that life and nature are extremely diverse sets of motions. Fidlin wrote “Any motion is deeply connected with one of the most fundamental properties of nature – its ability to react with oscillations at any internal change or external influence” [1]. In all areas of hu- man activities vibrational systems are increasingly abundant and varied and the study of those systems is always required. Most phenomena in our world are essentially nonlinear and described by nonlinear equations. We might simplify nonlinear phenomena as lin- ear ones to make them easier to understand; however, for further investigation nonlinear phenomena should be treated as nonlinear problems. Thus, the study of nonlinear prob- lems is of crucial importance not only in all areas of physics but also in engineering and in other disciplines. In particular, it appears that the analysis of vibration based on non- linear mathematical models requires appropriate methods. Therefore, new methods for analysis of nonlinear oscillations always cause concern of scientists and technicians. Re- cently, a dual approach has been proposed to study the response of nonlinear systems [2] c 2020 Vietnam Academy of Science and Technology 2 N. D. Anh and some dual techniques have been developed, e.g. [3–27], based on the concept of du- ality. Nature and life always contain dual inclinations. Those are perspectives that are contradictory, or complementary to each other. Natural phenomena and human activ- ities exhibit often dual characters which reflect two side processes or/and the relative balance of two opposite sides. For illustration we may say attack – defense in a football match, one way and return in an excursion, day and night. When a problem is consid- ered it is quite often that one its side is given too much attention while another side is almost or completely forgotten. This usual approach doesn’t reflect the real essence of the problem in question and hence doesn’t yield an expected solution in many cases. The main issue of a dual approach to a scientific problem is to always consider two different (dual) aspects of the problem. This allows the study to become more harmonious and reflects the essence of the problem. In the dual approach a dual technique is one that can introduce two dual perspectives for the same problem in consideration. Let one needs to investigate a problem. The use of the dual approach to this problem means that one should introduce a dual technique that can reflect the essence of the problem. This paper reviews key ideas of the reported researches on the dual approaches to the vibration analysis [3–27]. Various types of dual techniques, different implements and realizations of dual approaches to vibration analysis and control are reviewed. Finally, the challenging issues on the dual techniques are discussed. 2. DUAL EQUIVALENT REPLACEMENT The first introduction of the dual approach to the nonlinear vibrations was suggested in [2] for the problem of equivalent linearization. In science we usually needs to replace approximately an object A described by the function A(x) with the object B described by the function B(x). Thus, we will replace A(x) approximately with kB(x) where k is an equivalent replacement coefficient to be found from an equivalent replacement criterion, for example, by the mean-square error criterion D E e2 = (A(x) − kB(x))2 → min, (1) k where e = A(x) − kB(x) is the error of replacement, h·i is the deterministic averaging operator or expectation operator for the case of random functions A(x), B(x). If B(x) is a linear function of x, B(x) = x, the equivalent replacement is called equivale ... e some vibrating systems with nonlinear- ities. The strongly nonlinear Duffing oscillator with third, fifth, and seventh powers of the amplitude, the other strongly nonlinear oscillators and the cubic Duffing with discon- tinuity are considered. The results obtained via this method are compared with the ones achieved by the Min-Max Approach (MMA), the Modified Lindstedt – Poincare Method (MLPM), the Parameter – Expansion Method (PEM), the Homotopy Perturbation Method (HPM) and 4th order Runge–Kutta method. 10 N. D. Anh Further developments of this weighted averaging have been presented in [24,25] for nonlinear systems appearing in practical engineering and physical problems. In [26, 27] the equivalent linearization method with weighted averaging has been used to inves- tigate the nonlinear vibration of microbeams based on the nonlinear elastic foundation through the modified couple stress theory [26] and the nonlinear vibration of nanobeams under electrostatic force through the nonlocal strain gradient theory [17]. The obtained results demonstrate that this method is very convenient for solving nonlinear equations. Anh and Nguyen [6,7] suggested approximate analytical solutions of the optimal tuning ratio of the DVA for the H∞ optimization by using the idea of local averaging and dual replacement to the equivalent linearization method. Based on the idea of the weighted dual mean square error criterion, the authors of [8] give an analytical approach to the design of the three-element dynamic absorber for damped structures under ground motion by replacing the original damped structure by an equivalent undamped structure. Comparisons have been done to validate the accuracy of the obtained results. In [17] a simple method to determine the approximate analytical solutions of the nontraditional DVA when the damped primary structure is subjected to ground motion is proposed. The main idea is based on the dual mean square error criterion of the equivalent linearization method to replace approximately the original damped structure by an equivalent un- damped one. Comparisons have been done to validate the effectiveness of the obtained results. The global-local approach is used in [18] to give approximate analytical solutions of H∞ optimization for all standard, three-element and non-traditional DVAs attached to damped primary structures. The study is based on the global-local criterion of the equivalent linearization method in order to replace approximately the original damped structure by an equivalent undamped one. 4. SOME PERSPECTIVE ASPECS OF DUAL APPROACH In this section we suggest some further perspective research aspects of the dual ap- proach. First the weighted dual mean square error criterion has been investigated for many stochastic nonlinear systems; however, it wasn’t used to study deterministic non- linear vibrational systems. Thus, numerical simulations can be carried out to check the accuracy of this criterion for free and forced vibrations in those systems. A new expres- sion for the weighted parameter p different from (16) may be proposed to improve the accuracy of the weighted dual mean square error criterion. Similarly, the global-local mean square error criterion can be modified in order to be applicable to deterministic nonlinear vibrational systems. Second, comprehensive re- searches about the local averaging operator should be investigated for periodic functions. For ω-periodic function x(ωt) the conventional averaged value of x(ωt) over one period is defined as 2π/ω 2π ω Z 1 Z hx(ωt)i = x(ωt)dt = x(τ)dτ. (34) 2π 2π 0 0 A comprehensive review on dual approach to the vibration analysis: Some dual techniques and application 11 The local averaged value of x(ωt) is defined by replacing 2π in (34) by a positive value r r 1 Z hx(φ)i = x(φ)dφ, φ = ωt. (35) r r 0 If substituting the local averaging operator determined in (35) into the mean-square error criterion (1) for the equivalent replacement of A(ωt) by kB(ωt) one gets the local mean-square error criterion r 1 Z e2 = (A(φ) − kB(φ))2 dφ → min, (36) r r k 0 which leads to r Z A(φ)B(φ)dφ 0 k(r) = r . (37) Z B2(φ)dφ 0 The behavior of the equivalent replacement coefficient k(r) depending on the local value r needs to be investigated. The question of how r can be chosen is open and mini- mal values of k(r) are ones of interest. 5. CONCLUSIONS The study of nonlinear problems is of crucial importance not only in all areas of physics but also in engineering and in other disciplines. In particular, it appears that the analysis of vibration based on nonlinear mathematical models requires appropriate methods. Therefore, new methods for analysis of nonlinear oscillations always cause concern of scientists and technicians. Nature and life always contain dual inclinations. Those are perspectives that are contradictory, or complementary to each other. There- fore, scientific research also needs to reflect these properties. The main issue of a dual approach to a scientific problem is to always consider the two different (dual) aspects of the problem. This allows the study to become more harmonious and reflect the essence of the problem. In the dual approach a dual technique is one that can introduce two dual perspectives for the same problem in consideration. This paper reviews key ideas of the reported researches on the dual approaches to the vibration analysis. Three types of dual techniques, namely, forward - return dual technique, global-local dual technique, weighted averaging dual technique for the prob- lem of equivalent replacement are summarized. Different implements and realizations of dual techniques to nonlinear vibration analysis and design of dynamic absorbers are reviewed. Finally, the challenging issues based on the dual techniques are discussed. A number of possibilities for developing analytical techniques related to dual techniques 12 N. D. Anh are proposed. The review of the above studies shows that the dual approach is an ap- propriate one and the dual techniques are effective tools for studying random and deter- ministic nonlinear vibrational systems. Meanwhile the extension of the dual approach to other scientific problems is of high interest. ACKNOWLEDGEMENTS The paper is supported by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.04-2018.12. REFERENCES [1] A. Fidlin. Nonlinear oscillations in mechanical engineering. Springer Science & Business Media, (2005). [2] N. D. Anh. Duality in the analysis of responses to nonlinear systems. Vietnam Journal of Me- chanics, 32, (4), (2010), pp. 263–266. https://doi.org/10.15625/0866-7136/32/4/294. [3] N. D. Anh. Dual approach to averaged values of functions. Vietnam Journal of Mechanics, 34, (3), (2012), pp. 211–214. https://doi.org/10.15625/0866-7136/34/3/2361. [4] N. D. Anh, N. N. Hieu, and N. N. Linh. A dual criterion of equivalent linearization method for nonlinear systems subjected to random excitation. Acta Mechanica, 223, (3), (2012), pp. 645–654. https://doi.org/10.1007/s00707-011-0582-z. [5] N. D. Anh, V. L. Zakovorotny, N. N. Hieu, and D. V. Diep. A dual criterion of stochastic linearization method for multi-degree-of-freedom systems subjected to random excitation. Acta Mechanica, 223, (12), (2012), pp. 2667–2684. https://doi.org/10.1007/s00707-012-0738-5. [6] N. D. Anh and N. X. Nguyen. Extension of equivalent linearization method to design of TMD for linear damped systems. Structural Control and Health Monitoring, 19, (6), (2012), pp. 565– 573. https://doi.org/10.1002/stc.446. [7] N. D. Anh and N. X. Nguyen. Design of TMD for damped linear structures using the dual criterion of equivalent linearization method. International Journal of Mechanical Sciences, 77, (2013), pp. 164–170. https://doi.org/10.1016/j.ijmecsci.2013.09.014. [8] N. D. Anh, N. X. Nguyen, and L. T. Hoa. Design of three-element dynamic vibration absorber for damped linear structures. Journal of Sound and Vibration, 332, (19), (2013), pp. 4482–4495. https://doi.org/10.1016/j.jsv.2013.03.032. [9] N. D. Anh, L. X. Hung, and L. D. Viet. Dual approach to local mean square error crite- rion for stochastic equivalent linearization. Acta Mechanica, 224, (2), (2013), pp. 241–253. https://doi.org/10.1007/s00707-012-0751-8. [10] N. D. Anh, N. N. Linh, and N. Q. Hai. A weighted dual criterion for the problem of equiv- alent replacement. In Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis, Liverpool, UK, (2014), pp. 1913–1922, https://doi.org/10.1061/9780784413609.191. [11] N. D. Anh and N. N. Linh. A weighted dual criterion for stochastic equiva- lent linearization method. Vietnam Journal of Mechanics, 36, (4), (2014), pp. 307–320. https://doi.org/10.15625/0866-7136/36/4/5106. [12] N. D. Anh, I. Elishakoff, and N. N. Hieu. Extension of the regulated stochastic lin- earization to beam vibrations. Probabilistic Engineering Mechanics, 35, (2014), pp. 2–10. https://doi.org/10.1016/j.probengmech.2013.07.001. A comprehensive review on dual approach to the vibration analysis: Some dual techniques and application 13 [13] N. D. Anh and N. X. Nguyen. Design of non-traditional dynamic vibration absorber for damped linear structures. Journal of Mechanical Engineering Science, 228, (1), (2014), pp. 45–55. https://doi.org/10.1177/0954406213481422. [14] N. D. Anh, L. X. Hung, L. D. Viet, and N. C. Thang. Global–local mean square error criterion for equivalent linearization of nonlinear systems under random excitation. Acta Mechanica, 226, (9), (2015), pp. 3011–3029. https://doi.org/10.1007/s00707-015-1332-4. [15] N. D. Anh. Dual approach to averaged values of functions: A form for weighting coeffi- cient. Vietnam Journal of Mechanics, 37, (2), (2015), pp. 145–150. https://doi.org/10.15625/0866- 7136/37/2/6206. [16] N. M. Triet. Extension of dual equivalent linearization technique to flutter analysis of two dimensional nonlinear airfoils. Vietnam Journal of Mechanics, 37, (3), (2015), pp. 217–230. https://doi.org/10.15625/0866-7136/37/3/6474. [17] N. D. Anh and N. X. Nguyen. Research on the design of non-traditional dynamic vibration absorber for damped structures under ground motion. Journal of Mechanical Science and Tech- nology, 30, (2), (2016), pp. 593–602. https://doi.org/10.1007/s12206-016-0113-x. [18] N. D. Anh, N. X. Nguyen, and N. H. Quan. Global-local approach to the design of dynamic vibration absorber for damped structures. Journal of Vibration and Control, 22, (14), (2016), pp. 3182–3201. https://doi.org/10.1177/1077546314561282. [19] N. D. Anh, I. Elishakoff, and N. N. Hieu. Generalization of Seide’s problem by the regulated stochastic linearization technique. Meccanica, 52, (4-5), (2017), pp. 1003–1016. https://doi.org/10.1007/s11012-016-0421-3. [20] N. D. Anh, N. N. Hieu, P. N. Chung, and N. T. Anh. Thermal radia- tion analysis for small satellites with single-node model using techniques of equivalent linearization. Applied Thermal Engineering, 94, (2016), pp. 607–614. https://doi.org/10.1016/j.applthermaleng.2015.10.139. [21] P. N. Chung, N. D. Anh, N. N. Hieu, and D. V. Manh. Extension of dual equivalent lin- earization to nonlinear analysis of thermal behavior of a two-node model for small satel- lites in Low Earth Orbit. International Journal of Mechanical Sciences, 133, (2017), pp. 513–523. https://doi.org/10.1016/j.ijmecsci.2017.09.011. [22] N. D. Anh, N. Q. Hai, and D. V. Hieu. The equivalent linearization method with a weighted averaging for analyzing of nonlinear vibrating systems. Latin American Journal of Solids and Structures, 14, (9), (2017), pp. 1723–1740. https://doi.org/10.1590/1679-78253488. [23] N. D. Anh and N. N. Linh. A weighted dual criterion of the equivalent linearization method for nonlinear systems subjected to random excitation. Acta Mechanica, 229, (3), (2018), pp. 1297–1310. https://doi.org/10.1007/s00707-017-2009-y. [24] D. V. Hieu and N. Q. Hai. Analyzing of nonlinear generalized Duffing oscillators using the equivalent linearization method with a weighted averaging. Asian Research Journal of Mathe- matics, (2018), pp. 1–14. https://doi.org/10.9734/ARJOM/2018/40684. [25] D. V. Hieu, N. Q. Hai, and D. T. Hung. The equivalent linearization method with a weighted averaging for solving undamped nonlinear oscillators. Journal of Applied Mathematics, 2018, (2018). https://doi.org/10.1155/2018/7487851. [26] V.-H. Dang, D.-A. Nguyen, M.-Q. Le, and Q.-H. Ninh. Nonlinear vibration of mi- crobeams based on the nonlinear elastic foundation using the equivalent lineariza- tion method with a weighted averaging. Archive of Applied Mechanics, (2019), pp. 1–20. https://doi.org/10.1007/s00419-019-01599-w. [27] V.-H. Dang, D.-A. Nguyen, M.-Q. Le, and T.-H. Duong. Nonlinear vibration of nanobeams under electrostatic force based on the nonlocal strain gradient theory. International Journal 14 N. D. Anh of Mechanics and Materials in Design, (2019), pp. 1–20. https://doi.org/10.1007/s10999-019- 09468-8. [28] J. Lee Rodgers and W. A. Nicewander. Thirteen ways to look at the cor- relation coefficient. The American Statistician, 42, (1), (1988), pp. 59–66. https://doi.org/10.1080/00031305.1988.10475524. [29] J. B. Roberts and P. D. Spanos. Random vibration and statistical linearization. Dover Publications Inc., New York, (2003). [30] N. D. Anh and M. Di Paola. Some extensions of Gaussian equivalent linearization. In Inter- national Conference on Nonlinear Stochastic Dynamics, (1995), pp. 5–15. [31] L. X. Hung. Approximate analysis of some two-degree-of-freedom nonlinear random sys- tems by an extension of Gaussian equivalent linearization. Vietnam Journal of Mechanics, 23, (2), (2001), pp. 95–109. https://doi.org/10.15625/0866-7136/9943. [32] N. D. Anh and L. X. Hung. An improved criterion of Gaussian equivalent linearization for analysis of non-linear stochastic systems. Journal of Sound and Vibration, 1, (268), (2003), pp. 177–200. https://doi.org/10.1016/S0022-460X(03)00246-3. [33] N. Krylov and N. Bogoliubov. Introduction to nonlinear mechanics. Princeton University Press, New York, (1943). [34] S. H. Crandall. A half-century of stochastic equivalent linearization. Structural Control and Health Monitoring, 13, (1), (2006), pp. 27–40. https://doi.org/10.1002/stc.129. [35] I. Elishakoff and S. H. Crandall. Sixty years of stochastic linearization technique. Meccanica, 52, (1-2), (2017), pp. 299–305. https://doi.org/10.1007/s11012-016-0399-x. [36] L. Socha. Linearization methods for stochastic dynamic system. Lecture Notes in Physics, Springer, Berlin, (2008).
File đính kèm:
 a_comprehensive_review_on_dual_approach_to_the_vibration_ana.pdf
a_comprehensive_review_on_dual_approach_to_the_vibration_ana.pdf

